第6章 基于应变的单轴疲劳分析 11
引言
局部应变-寿命法的核心假设是:缺口构件的裂纹形核与小裂纹扩展阶段寿命,与光滑实验室试样在相同循环变形条件(即裂纹起始部位的局部应变控制材料行为)下的寿命一致。
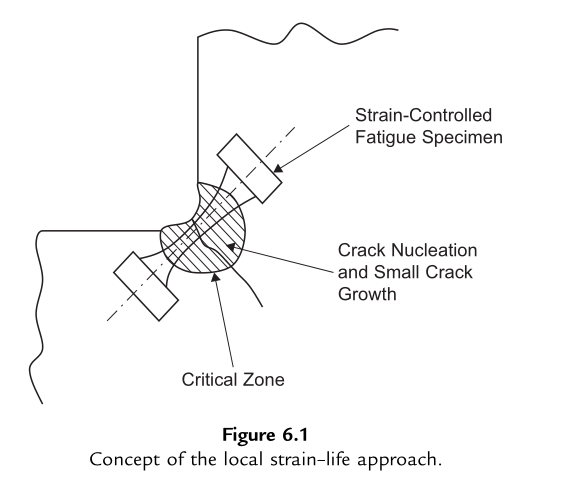
如图6.1所示,基于这一概念,若已知试样局部应变与疲劳寿命的关系,即可确定循环载荷作用下构件的疲劳起始寿命。这种局部应变-寿命关系通常以应变幅对疲劳寿命(以反向次数计)的双对数曲线表示,通过对光滑抛光的材料试样进行轴向循环应变控制试验获得。
循环应变控制试验之所以必要,是因为即使构件主体在循环载荷下表现为弹性行为,其应力集中区域的材料仍可能发生循环塑性变形。循环材料性能与疲劳材料性能的试验方案及数据处理方法可参考其他文献(Lee 等,2005),本章暂不涉及。
本章将按以下顺序介绍单轴应力状态下的局部应变-寿命法:循环应力-应变与疲劳性能估算、平均应力修正模型,以及缺口应力应变分析。
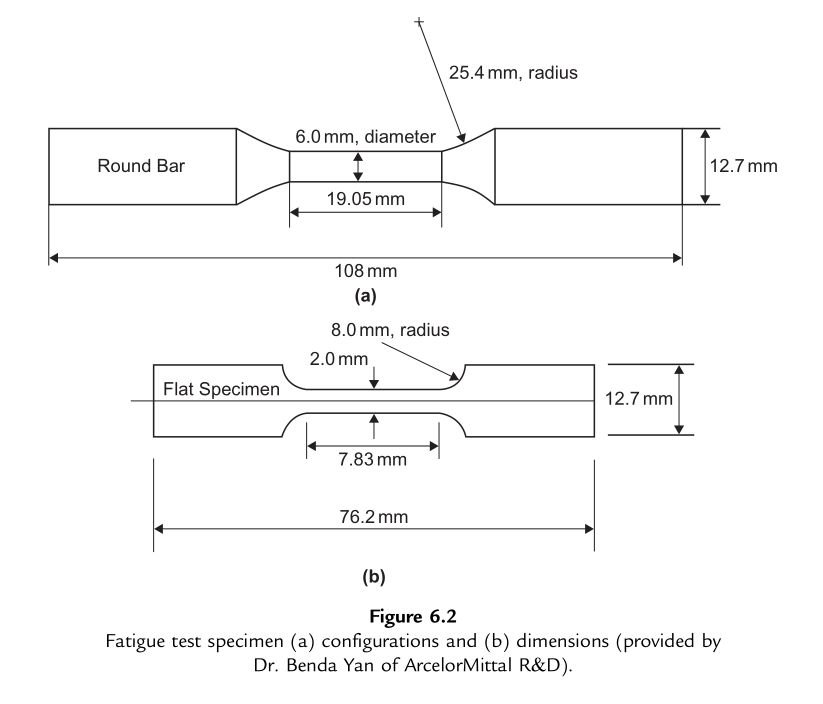
稳态循环应力-应变关系
对于大多数金属,疲劳寿命可通过稳态行为表征。在等幅应变控制试验中,材料经过初始循环的快速硬化或软化(约占总疲劳寿命的前几个百分点)后,应力-应变关系趋于稳定,这种循环稳定的应力-应变响应称为滞后回线,如图6.3所示。
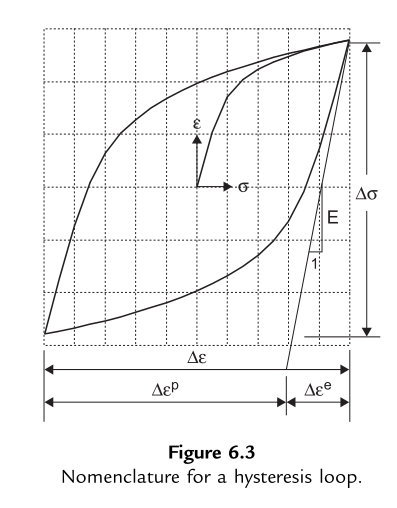
滞后回线由总应变范围(\(\Delta\varepsilon\))和总应力范围(\(\Delta\sigma\))界定,其内部区域代表材料在加载-卸载过程中产生的弹塑性功。通常取总疲劳寿命一半时的稳定滞后回线进行分析。假设总应变范围可分解为弹性应变分量(\(\Delta\varepsilon^e\))和塑性应变分量(\(\Delta\varepsilon^p\)),表达式如下:
其中,\(E\)为弹性模量。
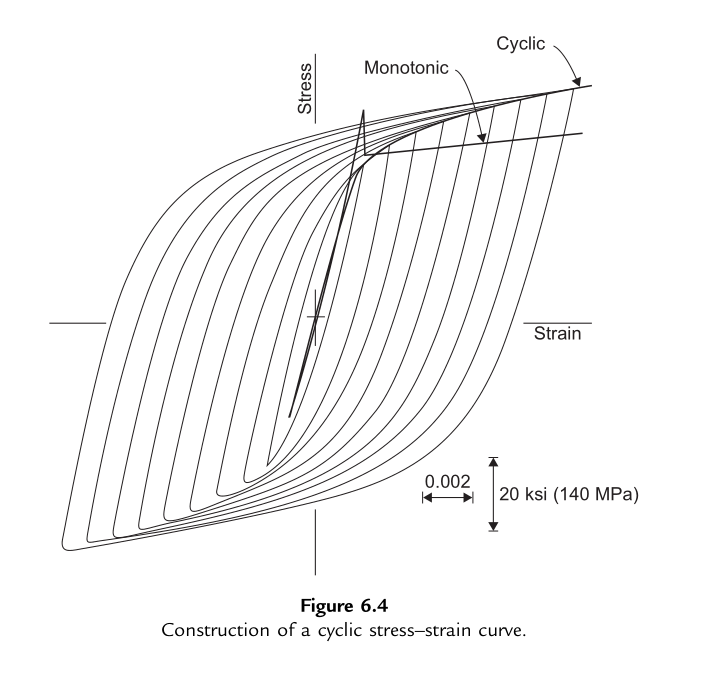
将不同应变幅下得到的一系列稳定滞后回线绘制在同一应力-应变坐标系中,连接各回线顶点即可得到循环应力-应变曲线(如图6.4所示),其数学表达式采用常用的Ramberg-Osgood方程:
其中,\(K'\)为循环强度系数;\(n'\)为循环应变硬化指数;上标“\('\)”表示与“循环行为”相关的参数,以区别于单调行为参数。
循环屈服应力(\(\sigma_y'\))定义为循环应力-应变曲线上塑性应变为0.2%时对应的应力。
Masing(1926)提出,应力幅(\(\sigma_a\))与应变幅(\(\varepsilon_a\))的关系遵循与循环应力-应变曲线相同的表达式:
其中,\(\varepsilon_a^e\)和\(\varepsilon_a^p\)分别为弹性应变幅和塑性应变幅。
Masing假设适用于拉压对称的均质材料。式(6.4)可改写为应变范围(\(\Delta\varepsilon\))和应力范围(\(\Delta\sigma\))的形式:
式(6.5)可进一步简化为以下形式:
对于给定的应变增量,可通过式(6.6)计算相对于参考转折点的应力增量,反之亦然。该式已广泛用于描述和追踪变幅载荷下的滞后行为。
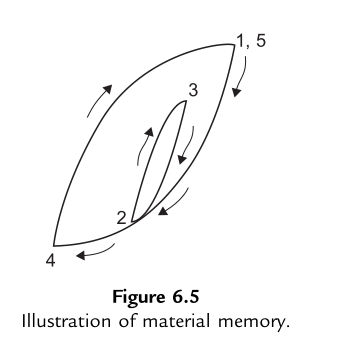
当材料响应回到先前经历过的变形状态时,会“记忆”到达该状态的路径,并在继续变形时沿该路径发展,这就是复杂载荷历史下材料表现出的“记忆效应”。在模拟过程中,需通过合理选择参考转折点来考虑这一效应。例如,如图6.5所示,在第三次反向(从点3到点4)中,当完成从点3到点2的小幅度反向后,应选取点1而非点3作为参考点,加载反向将沿点1到点4的路径进行。
完全反向、等幅应变-寿命关系
基于Morrow(1965)的研究,总应变幅(\(\varepsilon_a\))与失效疲劳寿命(以反向次数计,\(2N_f\))的关系可表示为:
其中,
\(\sigma_f'\)为疲劳强度系数;
\(\varepsilon_f'\)为疲劳延性系数;
\(b\)为疲劳强度指数;
\(c\)为疲劳延性指数。
上式称为零平均应力下的应变-寿命方程,是局部应变-寿命疲劳分析方法的基础。该方程由弹性应变幅-寿命曲线(\(\varepsilon_a^e\)-\(2N_f\))和塑性应变幅-寿命曲线(\(\varepsilon_a^p\)-\(2N_f\))叠加而成。
将Basquin(1910)提出的应变-寿命方程除以弹性模量\(E\),可得弹性应变幅-寿命曲线:
塑性应变幅-寿命曲线由Manson(1953)和Coffin(1954)同时提出,表达式为:
式(6.8)和式(6.9)均通过应力-寿命和塑性应变-寿命试验数据拟合得到,其中疲劳寿命\(2N_f\)为自变量。消去两式中的\(2N_f\),并与式(6.4)中的塑性应变幅对比,可得到以下估算关系:
将两条曲线绘制在双对数坐标系中均呈直线(如图6.6所示),两条直线的交点对应的疲劳寿命(以反向次数计)称为过渡疲劳寿命(\(2N_T\)),此时塑性应变幅与弹性应变幅的数值相等。
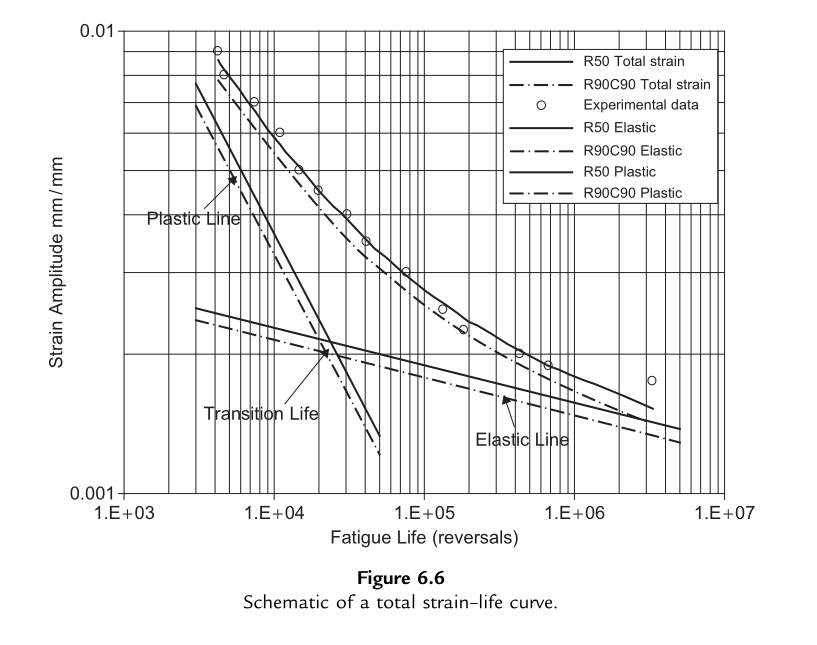
过渡疲劳寿命左侧(疲劳寿命小于\(2N_T\))为塑性应变主导区,即低周疲劳(LCF)区;右侧(疲劳寿命大于\(2N_T\))为弹性应变主导区,即高周疲劳(HCF)区。
总体而言,硬度和极限抗拉强度较高的钢材,其过渡疲劳寿命较低。令式(6.8)与式(6.9)相等,可估算过渡疲劳寿命:
循环材料性能与疲劳性能估算
若缺乏试验测得的应变-寿命疲劳数据,在设计阶段对材料的循环性能和疲劳性能进行估算具有重要意义,但这不能替代实际试验数据。Lee和Song(2006)对现有的估算方法(Muralidharan & Manson,1988;Baumel & Seeger,1990;Roessle & Fatemi,2000;Meggiolaro & Castro,2004)进行了综述和评估,得出结论:对于给定的极限抗拉强度(\(S_{t,u}\)),钢材和钛合金推荐采用均匀材料法则(Baumel & Seeger,1990),铝合金推荐采用中值法(Meggiolaro & Castro,2004)。两种方法的估算公式汇总于表6.1。
由于硬度与极限抗拉强度存在强相关性,已有多种模型用于通过硬度估算极限抗拉强度。Lee和Song(2006)的研究表明,Mitchell方程(Mitchell,1979)对钢材和铝合金均能提供最佳估算结果,其表达式为:
其中,\(HB\)为布氏硬度。
表6.1 基于均匀材料法则和中值法的循环材料性能与疲劳性能估算
| 材料性能 | 钢材¹ | 钛合金与铝合金¹ | 铝合金² |
|---|---|---|---|
| \(\sigma_f'\) | \(1.5S_{t,u}\) | \(1.67S_{t,u}\) | \(1.9S_{t,u}\) |
| \(b\) | \(-0.087\) | \(-0.095\) | \(-0.11\) |
| \(\varepsilon_f'\) | \(0.59\psi\) | \(0.35\) | \(0.28\) |
| \(c\) | \(-0.58\) | \(-0.069\) | \(-0.066\) |
| \(K'\) | \(1.65S_{t,u}\) | \(1.61S_{t,u}\) | - |
| \(n'\) | \(0.15\) | \(0.11\) | - |
注:若\(S_{t,u}/E \leq 310^{-3}\),则\(\psi=1\);若\(S_{t,u}/E > 310^{-3}\),则\(\psi=1.375 - 125.0(S_{t,u}/E)\);
¹均匀材料法则;²中值法
含平均应力的应变-寿命方程
多数试验数据表明,压应力平均应力对疲劳寿命有利,拉应力平均应力则对疲劳寿命有害。但实际影响取决于材料的损伤机制:对于对剪切参数敏感的材料,若压应力未与剪切面平行,则疲劳寿命不一定延长,这在弹性应变主导的高周疲劳区尤为明显。
结合局部应变-寿命法,已提出多种平均应力修正模型来量化平均应力对疲劳行为的影响。常用的模型包括修正Morrow方程(Morrow,1968)和Smith-Watson-Topper(SWT)模型(Smith 等,1970),具体如下:
Morrow模型
Morrow(1968)最初在应力-寿命方程中提出平均应力修正模型。该模型假设低周疲劳区平均应力影响可忽略,高周疲劳区平均应力影响显著,据此将应变-寿命方程修正为(即修正Morrow方程):
其中,\(\sigma_m\)为平均应力。
该方程已广泛应用于钢材,且在高周疲劳区取得了良好效果。Walcher、Gray和Manson(1979)发现,对于Ti-6Al-4V等其他材料,采用\(\sigma_f'\)进行平均应力修正时数值过高,因此引入中间参数\(k_m\sigma_f'\),提出通用公式:
该方程需要额外的试验数据来确定\(k_m\sigma_f'\)的值。
Smith-Watson-Topper模型
Smith、Watson和Topper(1970)提出了另一种平均应力修正模型,假设一个循环中的疲劳损伤由最大应力\(\sigma_{max}\)与应变幅\(\varepsilon_a\)的乘积决定,且完全反向试验中的\(\sigma_a\varepsilon_a\)与含平均应力试验中的\(\sigma_{max}\varepsilon_a\)相等。
1995年,Langlais和Vogel(1995)将该概念表示为:
其中,\(\sigma_{a,rev}\)和\(\varepsilon_{a,rev}\)分别为产生等效疲劳损伤的完全反向应力幅和应变幅。
\(\varepsilon_{a,rev}\)需从完全反向等幅应变-寿命曲线(式6.7)中获取,\(\sigma_{a,rev}\)需从循环应力-应变曲线(式6.3)中获取。当最大拉应力为零或负值时,SWT参数预测无疲劳损伤。式(6.16)可通过牛顿-拉夫逊迭代法求解。
对于满足疲劳性能与应变性能兼容性条件(即\(n'=b/c\)且\(K'=\sigma_f'/(\varepsilon_f')^{n'}\))的特殊情况,完全反向载荷下的最大拉应力为:
将完全反向等幅应变-寿命方程两边相乘,可得SWT平均应力修正公式:
式(6.18)是应用最广泛的SWT方程,已成功应用于灰铸铁(Fash & Socie,1982)、淬火碳钢(Koh & Stephens,1991)、微合金钢(Forsetti & Blasarin,1988)以及2000系和7000系沉淀硬化铝合金(Dowling,2009)。
示例6.1
在缺口板的缺口根部沿加载轴方向粘贴单个工作应变片。该缺口构件由SAE 1137碳钢制成,材料性能如下:
\(E=207\ \text{GPa}\),\(\sigma_y'=345\ \text{MPa}\),\(K'=1034\ \text{MPa}\),\(n'=0.15\),\(\sigma_f'=1517\ \text{MPa}\),\(\varepsilon_f'=0.90\),\(b=-0.10\),\(c=-0.65\)
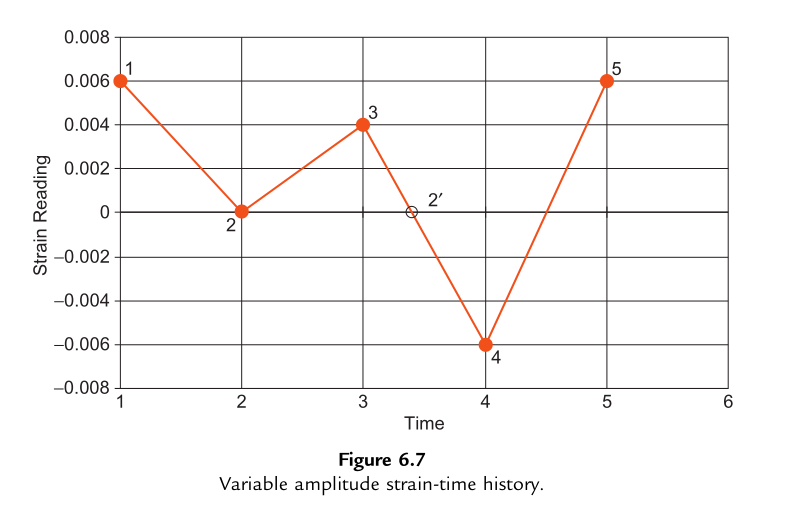
施加载荷产生的应变时程具有重复性,如图6.7所示。通过以下步骤确定SAE 1137缺口板的疲劳寿命:
- 绘制循环应力-应变响应(滞后回线);
- 采用SWT公式估算缺口板的疲劳寿命;
- 采用修正Morrow方程估算缺口板的疲劳寿命。
解答
循环加载过程中,假设材料初始加载遵循循环应力-应变曲线,后续加载反向遵循滞后应力-应变行为。对整个载荷块,按0.0006的应变增量计算应力。点1之前的应力-应变曲线采用循环应力-应变方程(Ramberg-Osgood方程)计算:
此后,所有相对于参考转折点的增量反向均基于Masing模型计算:
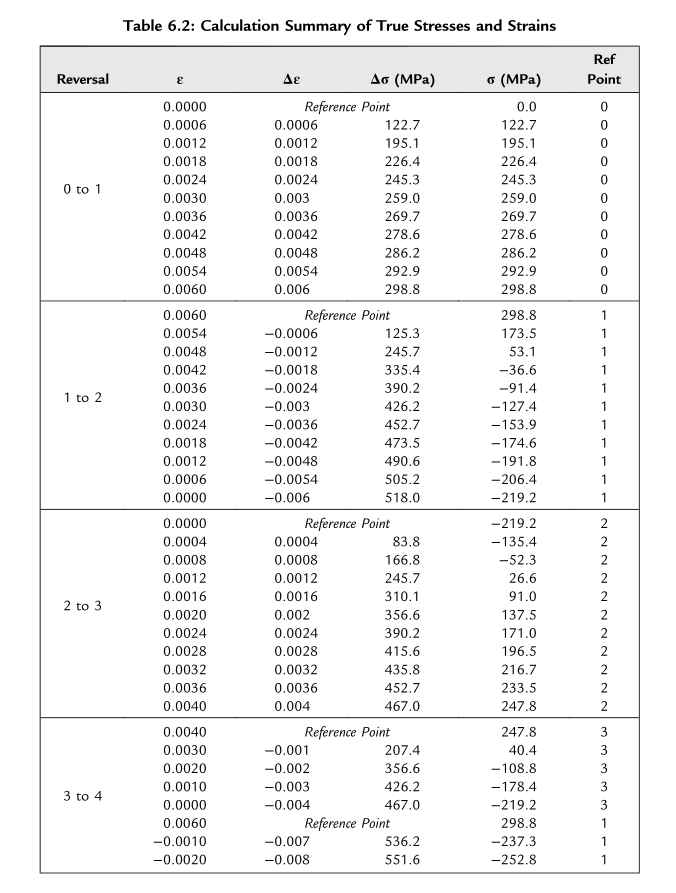
由于难以通过代数方法求解\(\sigma\)和\(\Delta\sigma\),采用Microsoft Excel的迭代求解工具进行计算。计算结果汇总于表6.2,其中列出了参考转折点以准确描述材料的记忆效应。从点1到点2(第一次反向),参考点为点1;从点2到点3(第二次反向),参考点更新为点2;从点3到点4的反向分为两部分:从点3到点2',再从点2'到点4。
点2'表示从参考点3返回的路径,由于材料的记忆效应,其与滞后回线上的点2等效。当完成从点3到点2的滞后回线闭合后,点1成为从点2'到点4剩余反向的参考点。最后,点4作为从点4到点5最后一次反向的参考点。表6.2列出了所有反向的计算应力和应变,并用于绘制单个载荷块循环的滞后回线(如图6.8所示)。
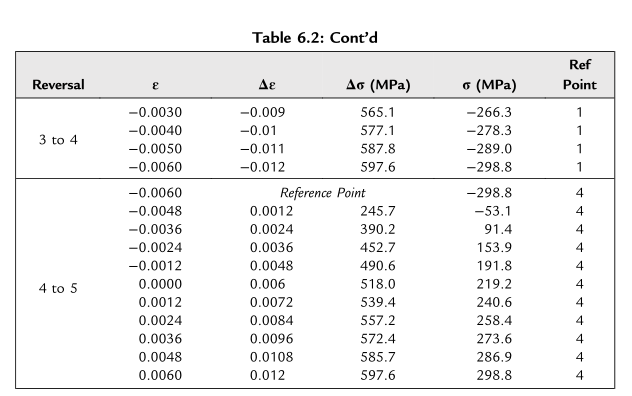
下一步需提取滞后回线,确定每个回线的最大/最小应力和应变点,为损伤计算提供数据。可采用三点雨流计数法验证识别的滞后回线。利用这些数据,通过Smith-Watson-Topper模型和修正Morrow方程评估构件能承受的载荷块循环次数。
对于每个计数循环,采用线性损伤累积法则(又称Palmgren-Miner线性损伤法则,Palmgren,1924;Miner,1945)计算单个损伤值。总损伤\(D\)定义为:
其中,\(n_i\)为施加于恒定应力幅的循环次数;\(k\)为应力块总数;\(N_{f,i}\)为通过修正Morrow方程或SWT模型计算得到的失效循环次数(疲劳寿命)。
当\(D=1\)时,认为构件发生失效,据此可估算给定载荷时程的重复次数(载荷块数量)。SWT模型和修正Morrow模型的损伤计算及寿命预测结果分别汇总于表6.3和表6.4。
表6.3 基于SWT参数的损伤计算汇总
| \(n_i\) | \(\varepsilon_{max}\) | \(\varepsilon_{min}\) | \(\sigma_{max}\ (\text{MPa})\) | \(\sigma_{min}\ (\text{MPa})\) | \(\varepsilon_a\) | \(N_f\ (\text{循环次数})\) | \(d_i\) |
|---|---|---|---|---|---|---|---|
| 1 | 0.004 | 0.000 | 368.3 | -317.7 | 0.002 | 194303 | \(5.1510^{-6}\) |
| 1 | 0.006 | -0.006 | 497.6 | -497.5 | 0.006 | 4476 | \(2.2310^{-4}\) |
每个载荷块的总损伤\(\sum d_i = 2.2810^{-4}\)
失效所需载荷块数量 = 4400
表6.4 基于修正Morrow参数的损伤计算汇总
| \(n_i\) | \(\varepsilon_{max}\) | \(\varepsilon_{min}\) | \(\sigma_{max}\ (\text{MPa})\) | \(\sigma_{min}\ (\text{MPa})\) | \(\sigma_m\ (\text{MPa})\) | \(\varepsilon_a\) | \(N_f\ (\text{循环次数})\) | \(d_i\) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.004 | 0.000 | 368.3 | -317.7 | 25.3 | 0.002 | 211905 | \(4.7210^{-6}\) |
| 1 | 0.006 | -0.006 | 497.6 | -497.5 | 0.005 | 0.006 | 4835 | \(2.0710^{-4}\) |
每个载荷块的总损伤\(\sum d_i = 2.1210^{-4}\)
失效所需载荷块数量 = 4700
缺口分析
缺口分析是指基于线弹性有限元分析(FEA)得到的伪(虚拟)应力时程,估算缺口根部(应力集中部位)局部应力-应变响应的数值分析方法。对于缺口几何形状明确的构件,伪应力(\(\sigma^e\))也可通过弹性应力集中系数(\(K_t\))与名义应力(\(S\))的乘积获得。
学者们已提出多种缺口分析方法以快速计算应力-应变,其中Neuber准则(Neuber,1961)和Molsky-Glinka能量密度法(Molsky & Glinka,1981)应用最为广泛,具体如下:
Neuber理论
Neuber(1961)分析了受单调扭转载荷的带槽构件,推导了缺口根部非线性材料行为的准则。Neuber的研究最初仅针对剪切参数,后续学者将其扩展至正应力和正应变参数。研究发现(如图6.9所示),局部屈服发生后,缺口根部的局部真实应力(\(\sigma\))小于弹性理论预测的伪应力,而局部真实应变(\(\varepsilon\))大于弹性理论估算值。
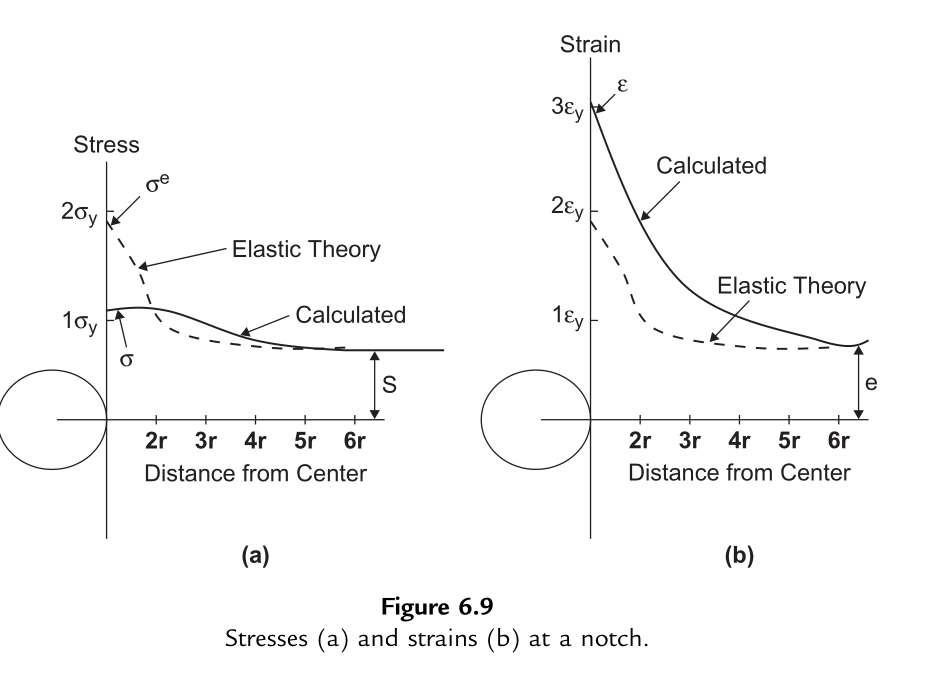
将局部真实缺口应力与名义应力(\(S\))的比值定义为真实应力集中系数(\(K_\sigma\)),局部真实缺口应变与名义应变(\(e\))的比值定义为真实应变集中系数(\(K_\varepsilon\))。Neuber提出假设:弹性应力集中系数是真实应力集中系数与真实应变集中系数的几何平均值,即:
对式(6.20)两边平方,得到著名的Neuber表达式:
Neuber准则的物理意义如图6.10所示(为便于图形说明,式(6.21)两边均除以2)。
循环加载过程中,假设材料初始加载遵循循环应力-应变曲线,后续加载反向遵循滞后应力-应变行为。因此,基于初始循环应力-应变曲线,Neuber方程可表示为:
基于滞后应力-应变曲线,Neuber方程可表示为:
其中,式(6.22)中的下标1表示初始循环加载条件。
式(6.22)和式(6.23)表示给定\(K_t\)和名义应力-应变数据时的双曲线方程,方程右侧通常称为Neuber常数。为求解两个未知量(\(\sigma_1\)和\(\varepsilon_1\),或\(\Delta\sigma\)和\(\Delta\varepsilon\)),还需引入循环材料行为的补充方程。以下将根据名义应力-应变行为讨论Neuber方程的应用。
名义弹性行为
当带缺口构件的主体表现为弹性,而塑性仅在缺口根部局部发生时(称为名义弹性行为),满足以下Neuber方程:
初始循环应力-应变曲线
滞后应力-应变曲线
其中
\(\mathrm{S}_1 =\) 初始加载的名义应力
\(\mathrm{e}_1 =\) 初始加载的名义应变
\(\sigma_1 =\) 初始循环加载曲线上的局部真实缺口应力
\(\varepsilon_1 =\) 初始循环加载曲线上的局部真实缺口应变
\(\Delta \mathrm{e} =\) 名义应变范围
\(\Delta \mathrm{S} =\) 名义应力范围
将弹性名义应力-应变关系与局部循环应力-应变关系(式(6.23)、(6.24)至(6.27))代入Neuber方程(式(6.22)和(6.23)),可得:
以及
已知\(\mathrm{K}_{\mathrm{t}}\)与名义应力或伪应力时,可通过Newton-Raphson迭代法求解局部应力。
一旦解出局部应力,式(6.25)或(6.27)将用于得到对应的局部应变值。
作为经验法则,当名义应力低于循环屈服应力的90%时,名义弹性行为的假设通常是适用的。
净截面名义整体屈服
当考虑净截面非线性行为时,名义应力(\(S\))和名义应变(\(e\))需遵循非线性材料关系,Neuber准则也需相应修正。Seeger和Heuler(1980)提出修正名义应力\(S^M\)以考虑整体屈服:
其中,\(K_p\)为极限载荷系数或塑性缺口系数,定义为:
\(L_y\)和\(L_p\)分别为净截面首次屈服和整体屈服对应的载荷。
可通过理想弹塑性材料的有限元分析确定\(L_p\)和\(L_y\)。修正后的应力和应变(\(S^M\)和\(e^M\))遵循循环应力-应变方程:
由于缺口伪应力与名义应力的定义无关,引入与\(S^M\)相关的修正弹性应力集中系数\(K^M\):
此时,Neuber准则可改写为:
将式(6.30)、式(6.32)和式(6.33)代入上式,整理得到:
式(6.35)为适用于净截面非线性行为的广义Neuber准则。若\(S^M\)-\(e^M\)曲线处于弹性范围,则\(\left(\frac{e^M E}{S^M}\right)=1\),广义Neuber方程退化为经典Neuber方程(式6.21)。
修正Neuber准则
为在局部应变-寿命法中考虑循环材料行为,Topper等(1969)提出将Neuber准则中的\(K_t\)替换为疲劳缺口系数(\(K_f\)),即修正Neuber准则。该方法因重复考虑缺口根部塑性效应以及将S-N经验关系引入“更具基础性的理论”而受到批评。但考虑到这些争议,仍推荐采用修正Neuber准则进行局部缺口应力-应变估算和疲劳寿命预测。
对于缺口几何形状复杂的构件,由于名义应力\(S\)和\(K_t\)难以量化,采用\(K_f\)的修正Neuber准则会面临挑战。但线弹性有限元分析可获得\(K_t S\)(伪应力),因此需将修正Neuber准则中的\(K_t S\)转换为\(K_f S\)。
\(K_t\)与\(K_f\)的关系仅能通过试验获得。以往已提出基于缺口半径(\(r\))和极限抗拉强度(\(S_{t,u}\))的经验平均应力模型(Peterson,1959;Neuber,1946;Heywood,1962)来估算\(K_t/K_f\)比值。此外,Siebel和Stieler(1955)提出以下\(K_t/K_f\)比值表达式:
其中,\(C_{ss}\)为取决于屈服强度(\(\sigma_y\))的材料常数;\(\overline{G}\)为相对应力梯度,定义为:
\(\sigma_{max}^e\)为局部最大伪应力;\(\sigma^e(x)\)为缺口根部附近的理论计算伪应力分布;\(x\)为距缺口根部的法向距离(如图6.11所示)。
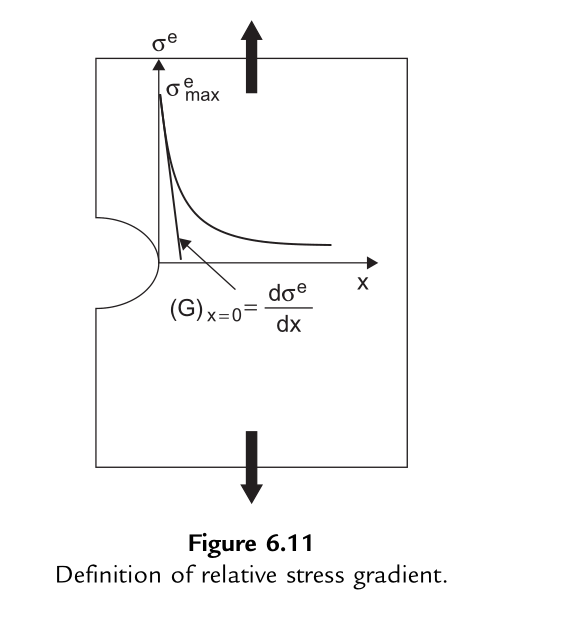
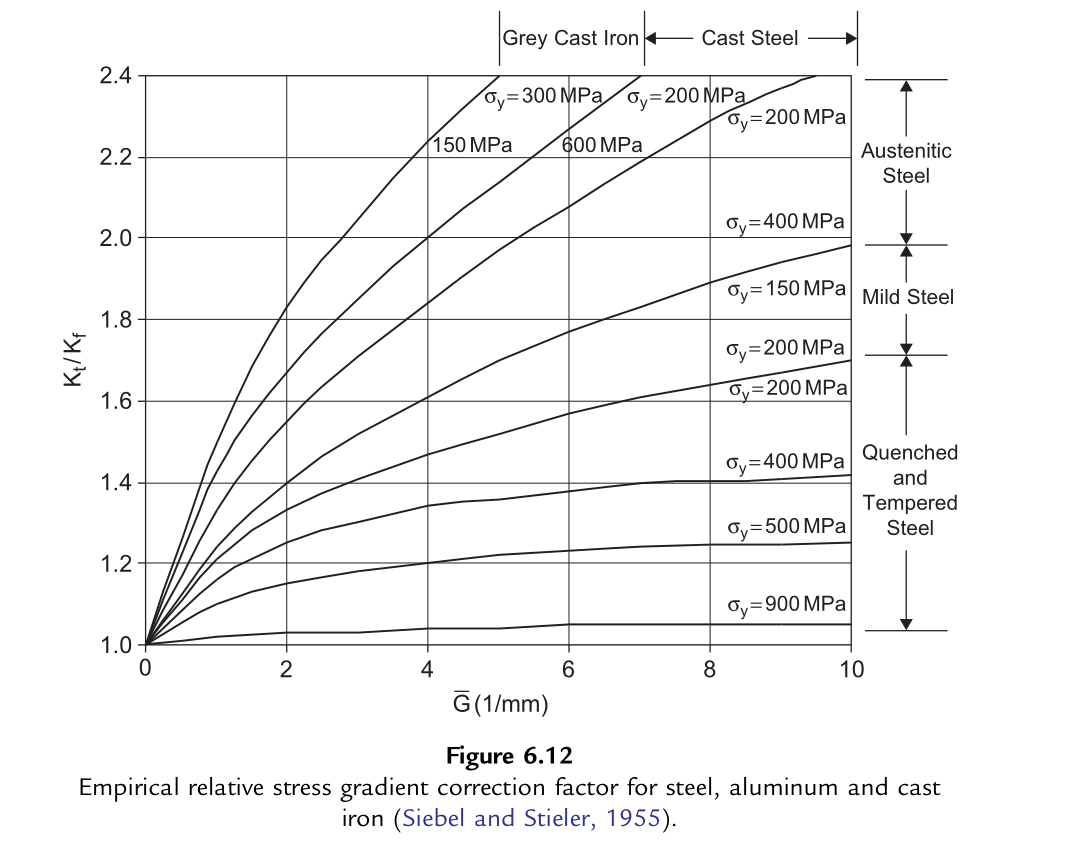
式(6.36)为适用于不同屈服强度材料的\(K_t/K_f\)比值通用公式,如图6.12所示。
\(K_t/K_f\)比值与\(\overline{G}\)的独特关系为修正Neuber模型提供了应用可能。对于给定的\(\overline{G}\)和材料屈服强度,可通过式(6.36)获得\(K_t/K_f\)比值;通过弹性有限元分析可获得缺口处的伪应力(\(\sigma_1^e=K_t S_1\))或伪应力范围(\(\Delta\sigma^e=K_t \Delta S\))。
令\(K_t/K_f=A_{SS}\),假设为名义弹性行为,修正Neuber方程可改写为:
这两个包含局部应力或应力范围应力梯度效应的方程可通过牛顿-拉夫逊迭代法求解。
Molsky-Glinka方法
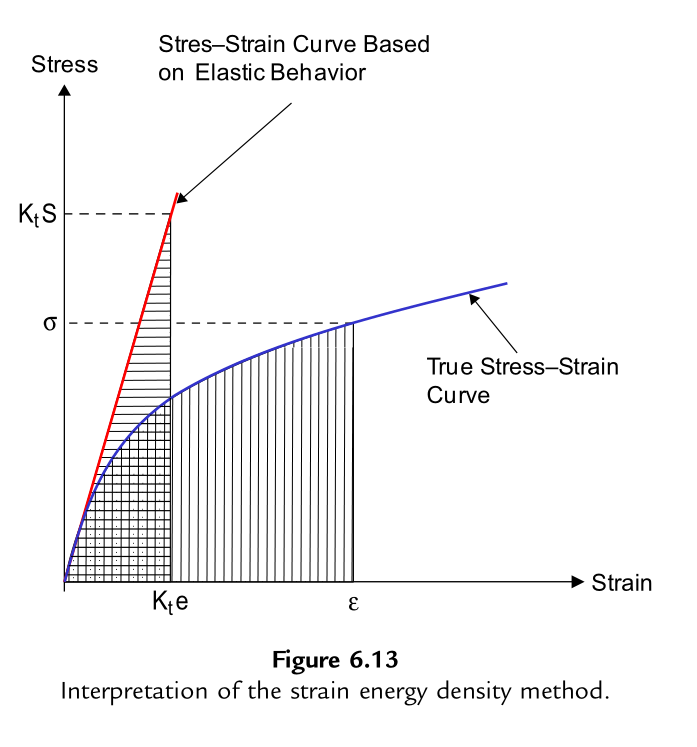
Molsky和Glinka(1981)提出了另一种缺口分析方法,假设缺口根部的应变能密度(\(W_e\))与名义应力应变产生的能密度(\(W_S\))成正比,比例系数为\(K_t^2\),即:
图6.13阐释了应变能密度法的物理意义。若假设带缺口试样表现为名义弹性行为,可得到如下应变能方程:
以及
将式(6.41)与式(6.42)代入式(6.40),可得到著名的能量密度公式:
对于初始加载,式(6.43)可简化为:
对于稳定滞后行为,式(6.43)可简化为:
其中,\(\sigma_1^{\mathrm{e}}\)与\(\Delta \sigma^{\mathrm{e}}\)是基于线弹性有限元分析得到的缺口根部局部伪应力与伪应力变化量。
示例6.2
对受载荷时程作用的缺口薄板进行线弹性有限元分析,结果表明单位施加载荷(\(P=1\)牛顿)下缺口根部的伪应力为0.035 MPa。该薄板由SAE 1005钢制成,循环性能和疲劳性能如下:
\(\mathrm{E} = 207,000\ \mathrm{MPa}\),\(\mathrm{K}^\prime = 1240\ \mathrm{MPa}\),\(\mathrm{n}^\prime = 0.27\),\(\sigma_{\mathrm{f}}^\prime = 886\ \mathrm{MPa}\),\(\mathrm{b} = -0.14\),\(\varepsilon_{\mathrm{f}}^\prime = 0.28\),\(\mathrm{c} = -0.5\)
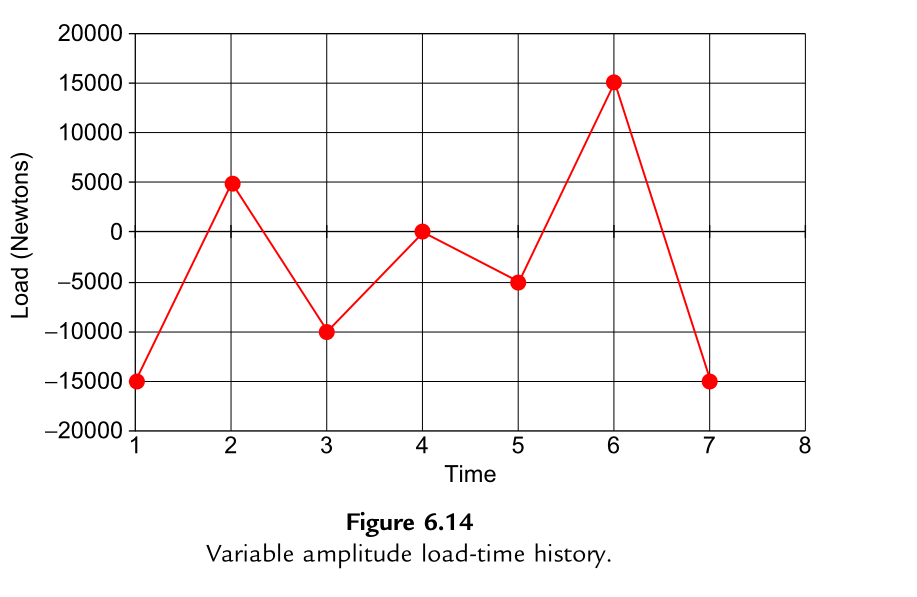
假设缺口薄板表现为名义弹性行为,在图6.14所示变幅载荷条件下,通过以下步骤估算SAE 1005钢缺口薄板的疲劳寿命:
-
采用Molsky-Glinka能量密度法模拟局部滞后行为;
-
采用SWT平均应力修正公式预测缺口板的疲劳寿命;
-
采用修正Morrow平均应力法预测缺口板的疲劳寿命。
![image]()
解答
对受载荷时程作用的缺口薄板进行线弹性有限元分析,结果表明单位载荷(\(P=1\ \text{N}\))下缺口根部的伪应力为0.035 MPa,因此所有施加载荷与局部伪应力呈线性关系。
根据该载荷时程及输入载荷与弹性应力的线性关系,可计算局部伪应力(\(\sigma^e\))。例如,第一个载荷点的伪应力为:
完整的伪应力时程如图6.15所示。
通过七个数据点构建滞后回线,每个反向分为10个部分以获得清晰的图形。采用Molsky-Glinka能量密度法将伪应力转换为真实应力和应变数据:取输入应力或应力变化量的绝对值,点1之前的初始加载曲线通过式(6.44)计算,此后所有相对于参考转折点的增量反向均基于式(6.45)计算。由于\(\sigma\)和\(\Delta\sigma\)难以通过代数方法求解,采用Microsoft Excel的迭代求解工具进行计算。
局部真实应力和应变的计算结果汇总于表6.5,得到的滞后回线如图6.16所示。需注意,计算增量反向时,需正确选择参考转折点以描述材料的记忆效应。
例如,模拟从点5到点6的反向时涉及三个参考点:点5、点3和点1分别作为以下反向段的参考点:点5到点4'、点4'到点2'、点2'到点6。点4'和点2'为记忆效应的返回点,与滞后回线上的点4和点2重合。通过三点雨流计数法可轻松识别这些参考点。
下一步需提取滞后回线,确定每个回线的最大/最小应力和应变点,为损伤计算提供输入数据。利用这些数据,通过SWT模型和修正Morrow平均应力修正模型评估载荷块循环次数。
对于每个计数循环,根据线性损伤法则计算单个损伤值,总和即为一个载荷块的总损伤。当损伤值达到1时定义为失效,因此一个载荷块总损伤的倒数即为失效前的载荷块循环次数。
计算结果汇总于表6.6和表6.7,其中SWT模型和修正Morrow模型分别预测构件在图6.14所示变幅载荷作用下,经过4900个和5100个载荷块后失效。
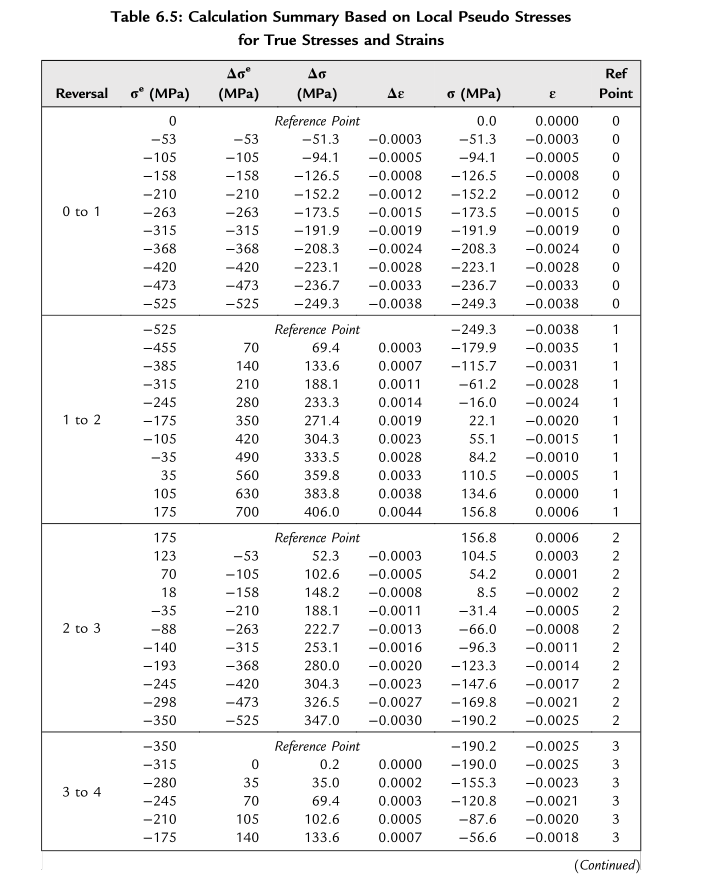
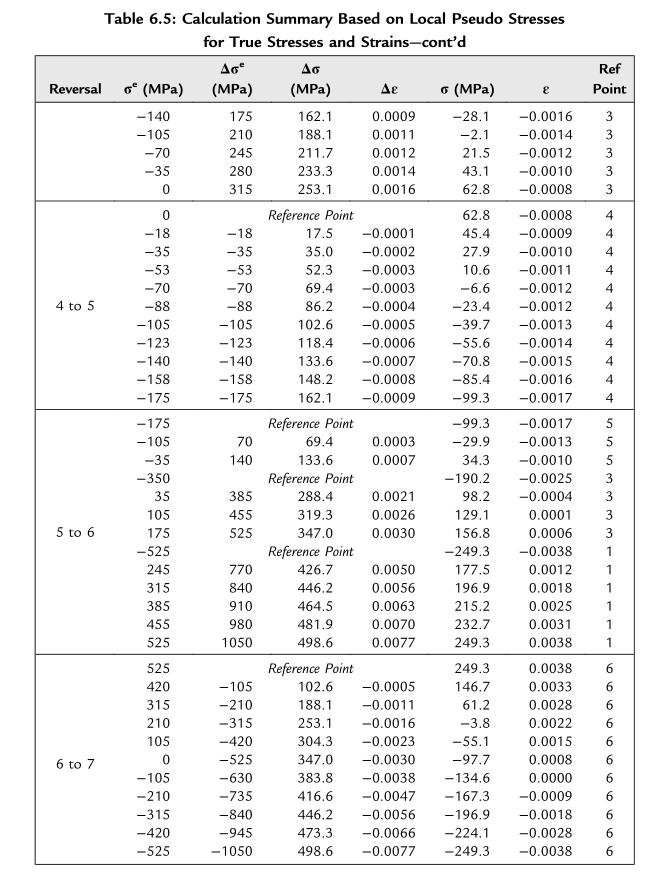
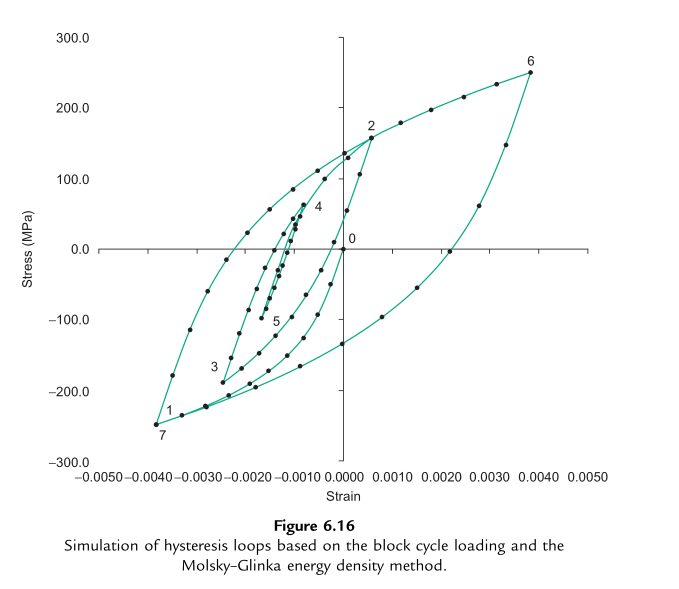
表6.6 基于SWT参数的损伤计算汇总
| \(n_i\) | \(\varepsilon_{max}\) | \(\varepsilon_{min}\) | \(\sigma_{max}\ (\text{MPa})\) | \(\sigma_{min}\ (\text{MPa})\) | \(\varepsilon_a\) | \(N_f\ (\text{循环次数})\) | \(d_i\) |
|---|---|---|---|---|---|---|---|
| 1 | -0.0008 | -0.0017 | 62.8 | -99.3 | 0.00043 | 3,215,072 | \(3.1110^{-8}\) |
| 1 | 0.000587 | -0.00246 | 156.8 | -190.2 | 0.00152 | 87,124 | \(1.1510^{-5}\) |
| 1 | 0.003831 | -0.00383 | 249.3 | -249.3 | 0.00383 | 5157 | \(1.9410^{-4}\) |
| 每个载荷块的总损伤\(\sum d_i = 2.0610^{-4}\) | |||||||
| 失效所需载荷块数量 = 4900 |
表6.7 基于修正Morrow参数的损伤计算汇总
| \(n_i\) | \(\varepsilon_{max}\) | \(\varepsilon_{min}\) | \(\sigma_{max}\ (\text{MPa})\) | \(\sigma_{min}\ (\text{MPa})\) | \(\sigma_m\ (\text{MPa})\) | \(\varepsilon_a\) | \(N_f\ (\text{循环次数})\) | \(d_i\) |
|---|---|---|---|---|---|---|---|---|
| 1 | -0.0008 | -0.0017 | 62.8 | -99.3 | -18.2 | 0.00043 | 1,700,984 | \(5.8810^{-8}\) |
| 1 | 0.00058 | -0.0024 | 156.8 | -190.2 | -16.7 | 0.00152 | 78,444 | \(1.2710^{-5}\) |
| 1 | 0.00383 | -0.00383 | 349.3 | -249.3 | 0 | 0.00383 | 5508 | \(1.8210^{-4}\) |
| 每个载荷块的总损伤\(\sum d_i = 1.9510^{-4}\) | ||||||||
| 失效所需载荷块数量 = 5100 |
应用
实际结构的表面状态受制造和加工工艺影响,与用于测定应变-寿命疲劳性能的光滑抛光试样不同。因此,需考虑残余应力、表面处理和表面粗糙度对高周疲劳的影响。以下介绍几种考虑这些因素的实用缺口分析模型。
残余应力影响
若制造工艺导致缺口根部存在残余应力(\(\sigma_r\))或残余应变(\(\varepsilon_r\)),且在施加工作载荷反向前已确定该残余应力或应变,则需修正初始加载的修正Neuber准则和Molsky-Glinka能量密度法。基于修正Neuber准则,已提出以下几种修正形式:(1. Lawrence等人(1982):
- Reemsnyder(1981):
- Baumel与Seeger(1989):
表面光洁度的影响
若表面处理因子(\(\mathrm{C}_{\mathrm{S}}\))与粗糙度修正因子(\(\mathrm{C}_{\sigma,\mathrm{R}}\))可从FKM指南(Haibach,2003)中获取,可对Lawrence模型进行修正以考虑表面光洁度的影响:
其中
根据FKM指南,钢与铸铁材料的表面处理因子列于表6.8中。表中的数值适用于直径30至40 mm的构件,括号内的数值则适用于直径8至15 mm的构件。
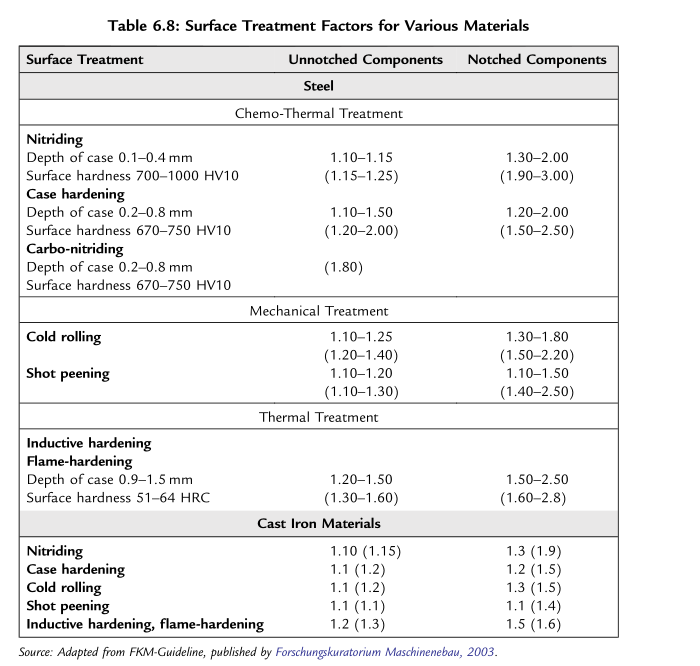
根据FKM指南,正应力下的粗糙度系数为:
其中,\(a_R\)为粗糙度常数(见表6.9);\(R_z\)为表面平均粗糙度(μm);\(S_{t,u}\)为极限抗拉强度(MPa);\(S_{t,min,u}\)为表6.9中给出的最小极限抗拉强度(MPa)。
表6.9 不同材料的\(a_R\)和\(S_{t,min,u}\)值
| 材料 | \(a_R\) | \(S_{t,min,u}\ (\text{MPa})\) |
|---|---|---|
| 钢材 | 0.22 | 400 |
| 铸钢 | 0.20 | 400 |
| 球墨铸铁 | 0.16 | 400 |
| 可锻铸铁 | 0.12 | 350 |
| 灰铸铁 | 0.06 | 100 |
| 变形铝合金 | 0.22 | 133 |
| 铸造铝合金 | 0.20 | 133 |
轧制表面、锻造表面和铸铁表面的平均粗糙度\(R_z=200\ \mu\text{m}\);钢材的磨削表面粗糙度为1-12 μm,加工表面粗糙度为6.3-100 μm。
总结
本章介绍了用于描述和追踪均质材料在变幅载荷时程下滞后行为的Masing方程。对于任意给定的应变增量,可通过该方程简便计算相对于参考转折点的应力增量,反之亦然。在材料模拟过程中,合理选择参考转折点以考虑复杂载荷条件下材料的记忆效应至关重要。
阐述了零平均应力下的Morrow应变-寿命方程,并结合局部应变-寿命法,提出了用于量化平均应力对疲劳行为影响的修正Morrow方程和SWT模型。
若缺乏试验测得的应变-寿命疲劳数据,设计阶段可对材料的循环性能和疲劳性能进行估算。对于给定的极限抗拉强度(\(S_{t,u}\)),钢材和钛合金推荐采用Baumel和Seeger(1990)的均匀材料法则,铝合金推荐采用Meggiolaro和Castro(2004)的中值法。
修正Neuber准则和Molsky-Glinka能量密度法是两种基于线弹性有限元分析伪应力时程,估算应力集中区域真实应力-应变行为的常用技术,本章讨论了其局限性和应用场景。此外,还介绍了考虑残余应力、表面处理和表面粗糙度对高周疲劳影响的实用缺口分析模型。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号