动态系统 MATLAB 例子

例2.4 现在讨论图2.1所示的机械系统。该系统一开始处于静止状态。位移x和y从它们各自的平衡位置开始测量。假设力p(t)是阶跃输入，位移x(t)是输出，试求该系统的传递函数。
然后，假设m = 0.1 kg，b₂ = 0.4 N·s/m，k₁ = 6 N/m，k₂ = 4 N/m，并假设p(t)是幅值为10 N的阶跃力，求出解析解x(t)。

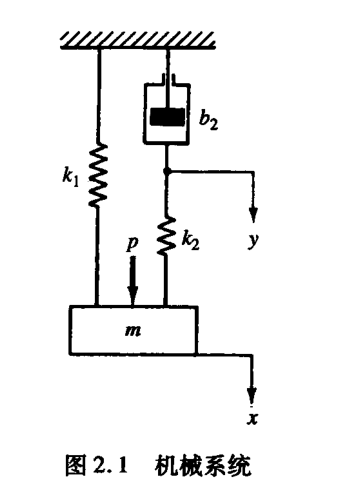
该系统的运动方程为

\[m\ddot{x} + k_1x + k_2(x - y) = p \]

\[k_2(x - y) = b_2\dot{y} \]

在零初始条件的假设下对这两个方程进行拉普拉斯变换，可以得到

\[(ms^2 + k_1 + k_2)X(s) = k_2Y(s) + P(s) \]

\[k_2X(s) = (k_2 + b_2s)Y(s) \]

从式(2.3)解得Y(s)并将其代入式(2.2)，可得

\[(ms^2 + k_1 + k_2)X(s) = \frac{k_2^2}{k_2 + b_2s}X(s) + P(s) \]

或者

\[[(ms^2 + k_1 + k_2)(k_2 + b_2s) - k_2^2]X(s) = (k_2 + b_2s)P(s) \]

由此可以得到传递函数

\[\frac{X(s)}{P(s)} = \frac{b_2s + k_2}{mb_2s^3 + mk_2s^2+(k_1 + k_2)b_2s + k_1k_2} \]

将\(m\)，\(k_1\)，\(k_2\)和\(b_2\)的给定数值代入式(2.4)，可以得到

\[\frac{X(s)}{P(s)} = \frac{0.4s + 4}{0.04s^3 + 0.4s^2 + 4s + 24} = \frac{10s + 100}{s^3 + 10s^2 + 100s + 600} \]

由于\(P(s)\)是幅值为10 N的阶跃力，所以

\[P(s) = \frac{10}{s} \]

于是，从式(2.5)可得

\[X(s) = \frac{10s + 100}{s^3 + 10s^2 + 100s + 600} \cdot \frac{10}{s} \]

为了求得解析解，需要将X(s)展开成为部分分式。为此，可以采用如下MATLAB程序来求留数、极点和直接项：

>> num = [100 1000];
>> den = [1 10 100 600 0];
>> [r,p,k] = residue(num, den)

结果：

r =
  -0.6845 + 0.2233i
  -0.6845 - 0.2233i
  -0.2977
  1.6667

p =
  -1.2898 + 8.8991i
  -1.2898 - 8.8991i
  -7.4204
  0

k =
  []

根据该MATLAB输出，\(X(s)\)可以被写成：

\[X(s) = \frac{-0.6845 + j0.2233}{s + 1.2898 - j8.8991} + \frac{-0.6845 - j0.2233}{s + 1.2898 + j8.8991} + \frac{-0.2977}{s + 7.4204} + \frac{1.6667}{s} \]

\[X(s) = \frac{-1.3690(s + 1.2898) - 3.9743}{(s + 1.2898)^2 + 8.8991^2} + \frac{-0.2977}{s + 7.4204} + \frac{1.6667}{s} \]

对\(X(s)\)进行拉普拉斯逆变换就可以得到：

\[x(t) = -1.3690e^{-1.2898t} \cos(8.8991t) - 0.4466e^{-1.2898t} \sin(8.8991t) - 0.2977e^{-7.4204t} + 1.6667 \]

其中\(x(t)\)的单位是米，时间\(t\)的单位是秒。这就是该问题的解析解。

参考文献

控制理论MATLAB教程 KO