控制之美1-第七章 PID控制

目录

• 7.1 引子
• 7.2 比例控制
• 7.3 比例积分控制器

7.1 引子

\[7000 \frac{dx(t)}{dt}+10ax(t)=u(t)+d(t) \]

\(u(t)\) 是体重变化，

\(u(t)=E_i-E_a\), \(E_i\) 是热 量摄入 ,\(E_a\) 是运动消耗,

\(x(t)\) 系统输出，体重

\(a\)是劳动强度系数

\(d(t)=-aC\) 是扰动量

进行拉普拉斯变换

\[7000(sX(s)-x_0)+10asX(s)=U(s)+D(s) \]

\[→ (7000s+10a)X(s)=U(s)+D(s)+7000ax_0 \]

\(x_0\) 是初始体重，

传递函数

\[G(s)=\frac{X(s)}{U(s)+D(s)+7000x_0}=\frac{1}{7000s+10a} \]

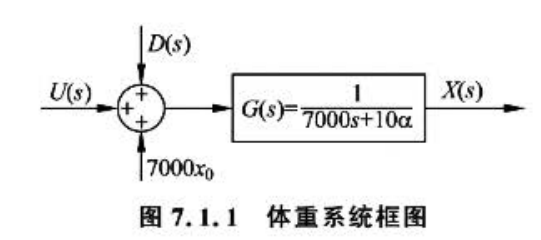
其中\(U(s)\) 和 \(D(s)\)是以 阶跃形式作用在系统上 ，
初 始状态\(7000x_0\),则是以 冲激方 式作用 在系统上。

\(G(s)\) 的特征方程为

\[7000s + 10a =0 \]

\[s_p= -\frac{a}{100}<0 \]

7.2 比例控制

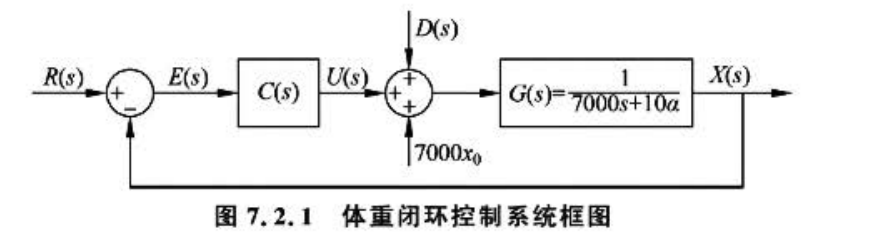
r(t)是目标体重(参考值)，r(t)=r=65kg,对应的拉普拉斯变换\(R(s)=\frac{r}{s}\)

\(e(t)=r(t)-x(t)\)是误差（参考值与输出之家的差距），对应的拉普拉斯变换\(E(s)=R(s)-X(s)\)

\(C(s)\)是控制器，包含了我们需要设计的算法

人们在控制体重时会很自然地想到一种 策略-当体重大于目标值的时候， 那就多运动.
少吃饭 ，而且超重得越多 ，就越要多运动， 越要少吃饭， 反之亦然。 这 种简单粗暴的策略被
称为比例控制( Proportionz Controller) .

比例控制是一种简单的控制方式，其控制量为误差的线性函数：

\[u(t)=K_{P}e(t) \]

\(K_{P}\) 为比例增益， $ e(t)$ 为误差。

在拉普拉斯变换域中，比例控制可以表示为：

\[U(s)=K_{P}E(s) \]

此时，系统的输出可以表达为：

\[X(s) = \frac{U(s)+D(s)+7000x_0}{7000s + 10\alpha} = \frac{E(s)K_p + D(s)+7000x_0}{7000s + 10\alpha} = \frac{(R(s) - X(s))K_p + D(s)+7000x_0}{7000s + 10\alpha} \]

\[\Rightarrow X(s) = \frac{K_pR(s)+D(s)+7000x_0}{7000s + 10\alpha + K_p} \quad (7.2.2) \]

根据前面的定义，\(d(t)=-\alpha C\)，可得\(D(s)=-\frac{\alpha C}{s}\)。又已知\(R(s)=\frac{r}{s}\)，式(7.2.2)变为：

\[X(s) = \frac{K_pr - \alpha C + 7000x_0s}{s(7000s + 10\alpha + K_p)} \quad (7.2.3) \]

根据式(7.2.3)，\(X(s)\)有两个极点，分别为\(s_{p1}=0\)和\(s_{p2}=-\frac{10\alpha + K_p}{7000}\)。其中，\(s_{p1}\)是输入\(U(s)\)和扰动\(D(s)\)的极点，\(s_{p2}\)是闭环传递函数的极点。对式(7.2.3)进行部分分式分解，可得：

\[X(s)=\left(\frac{K_pr - \alpha C}{K_p + 10\alpha}\right)\frac{1}{s}+\left(\frac{x_0 - \frac{K_pr - \alpha C}{K_p + 10\alpha}}{7000}\right)\frac{1}{s+\frac{K_p + 10\alpha}{7000}} \quad (7.2.4) \]

对式(7.2.4)进行拉普拉斯逆变换，得到：

\[x(t)=\mathcal{L}^{-1}[X(s)]=\frac{K_pr - \alpha C}{K_p + 10\alpha}+\left(x_0 - \frac{K_pr - \alpha C}{K_p + 10\alpha}\right)e^{-\frac{K_p + 10\alpha}{7000}t} \quad (7.2.5) \]

在式(7.2.5)中，输出\(x(t)\)的稳定性与传递函数的极点\(s_{p2}=-\frac{10\alpha + K_p}{7000}\)相关。在本例中，\(K_p>0\)，因此\(s_{p2}<0\)。说明随着时间的增加，\(e^{-\frac{K_p + 10\alpha}{7000}t}\)项将趋于零。因此，可以通过式(7.2.5)得到系统输出的终值，即：

\[x(\infty)=\lim_{t \to \infty} x(t)=\lim_{t \to \infty} \left( \frac{K_p r - \alpha C}{K_p + 10 \alpha} + \left( x_0 - \frac{K_p r - \alpha C}{K_p + 10 \alpha} \right) e^{-\frac{K_p + 10 \alpha}{7000}t} \right) \]

\[= \frac{K_p r - \alpha C}{K_p + 10 \alpha} \quad (7.2.6) \]

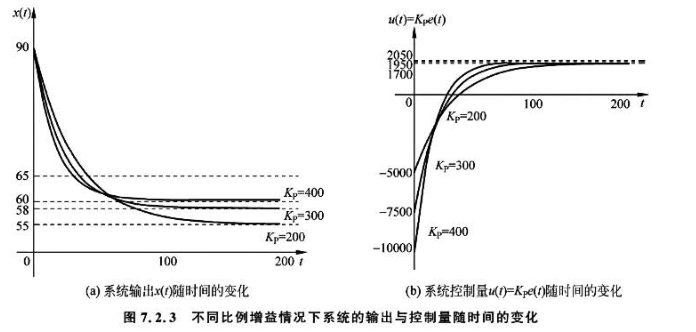
图7.2.3(a)呈现了在不同\(K_p\)下系统输出\(x(t)\)随时间的变化（其中，初始体重\(x_0 = 90kg\)，目标体重\(r = 65kg\)，其余条件参考表7.1.1案例1）。式(7.2.6)和图7.2.3(a)说明比例增益\(K_p\)越大，系统的终值\(x(\infty)\)越接近于参考值\(r\)。图7.2.3(b)显示了不同\(K_p\)下的系统控制量\(u(t)\)随时间的变化。

图片中的文字主要是关于控制系统中稳态误差（Steady State Error）的推导和分析。

1. 稳态误差的定义和推导

   • 稳态误差\(e_{ss}\)定义为系统误差的终值，即\(e_{ss}=e(\infty)=r - x(\infty)\)，其中\(r\)是参考输入，\(x(\infty)\)是系统输出的终值。
   • 根据之前的推导（7.2.6），\(x(\infty)=\frac{K_p r - \alpha C}{K_p + 10 \alpha}\)。
   • 将\(x(\infty)\)代入稳态误差的定义式，得到：
     \[e_{ss}=r - \frac{K_p r - \alpha C}{K_p + 10 \alpha}=\frac{10 \alpha r + \alpha C}{K_p + 10 \alpha} \]

   • 这表明比例增益\(K_p\)越大，稳态误差\(e_{ss}\)越小，与图7.2.3(a)所示的现象一致（\(K_p\)越大，输出的终值\(x(\infty)\)越靠近参考值\(r\)）。
   • 当\(K_p \to \infty\)时，\(e_{ss}=0\)。

2. 实际情况中的限制

   • 在实际情况中，\(K_p\)不可能无限地增大，例如在这个例子中每天的热量摄入和运动都是有限的。
   • 这决定了比例控制的局限性，它无法消除稳态误差。需要引入新的手段和方法来解决这个问题。

总的来说，这段文字通过数学推导说明了比例控制下稳态误差与比例增益\(K_p\)的关系，并指出了在实际应用中比例控制的局限性。

7.3 比例积分控制器