B树

• B树

B树其实是一种多路查找树，它的每个结点可以拥有多个孩子而不是像二叉树那样最多只能拥有两个孩子，同时相对应的每个结点拥有多个元素以分出多个孩子。

其中B树中结点最大的孩子数目被称为B树的阶m。例如下图就是一个五阶B树（最右边的叶子结点拥有5个孩子）。

 

 

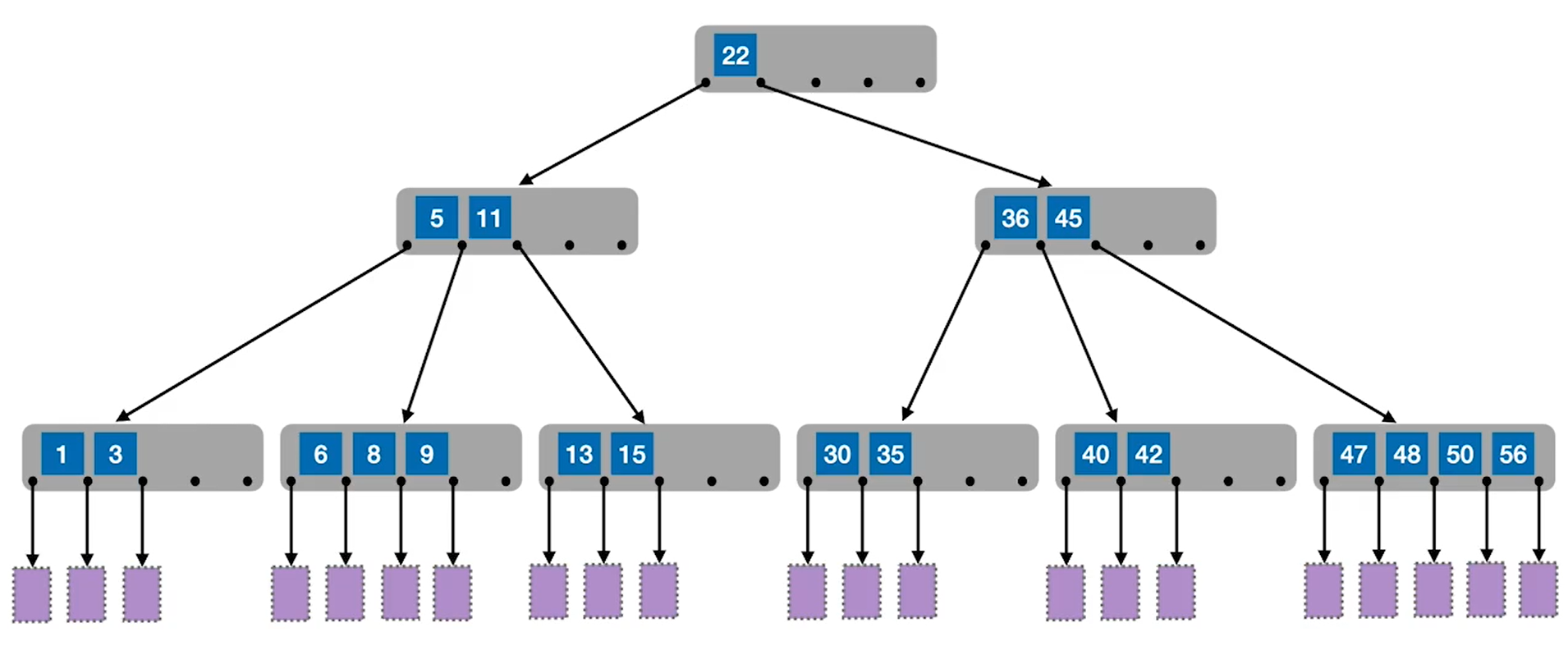
B树的性质

1. 如果根结点不是叶结点，则其至少有两棵子树。（为了满足第三个性质）
2. 每一个非根的分支结点都有k-1个元素和k个孩子（k-1个元素划分k个段，即k个孩子），其中[m/2]≤k≤m。每一个叶子结点n都有k-1个元素，其中[m/2]<k≤m。
3. 所有叶子结点都位于同一层次。（最重要！！！！）
4. 所有分支结点包含下列信息数据（n,Ao,Kp,A,,Kz,A2…,K.A)，其中:K;(i=1,2,…,n)为关键字，且K<K1(i=1,2,…,n-1);A (i=0,2,…,n)为指向子树根结点的指针，且指针A.所指子树中所有结点的关键字均小于K(i=1,2,…,n)，A。所指子树中所有结点的关键字均大于K,n(Im/2]-1≤n≤m-1)为关键字的个数(或n+1为子树的个数)。

B树的插入和删除

• 插入

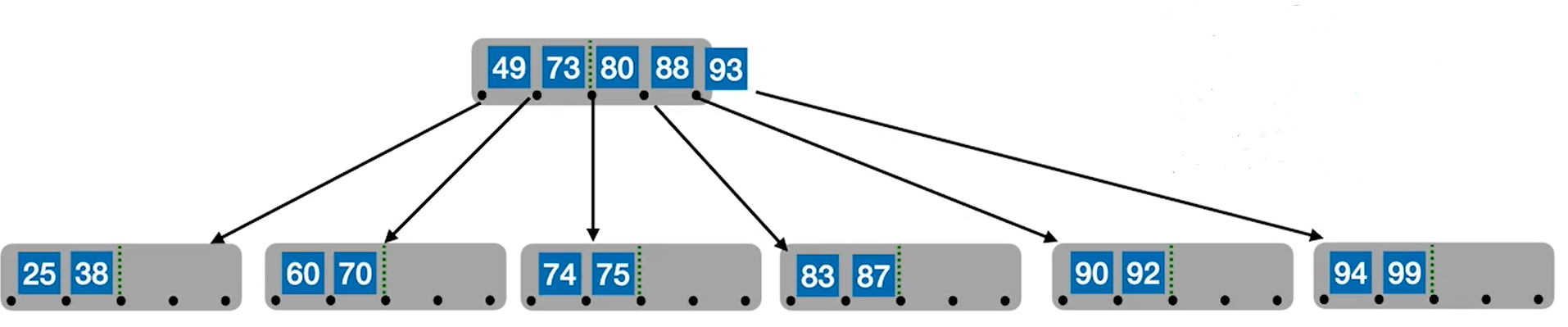
如图是一个五阶B树，现在要将70放入B树中

 

 

 

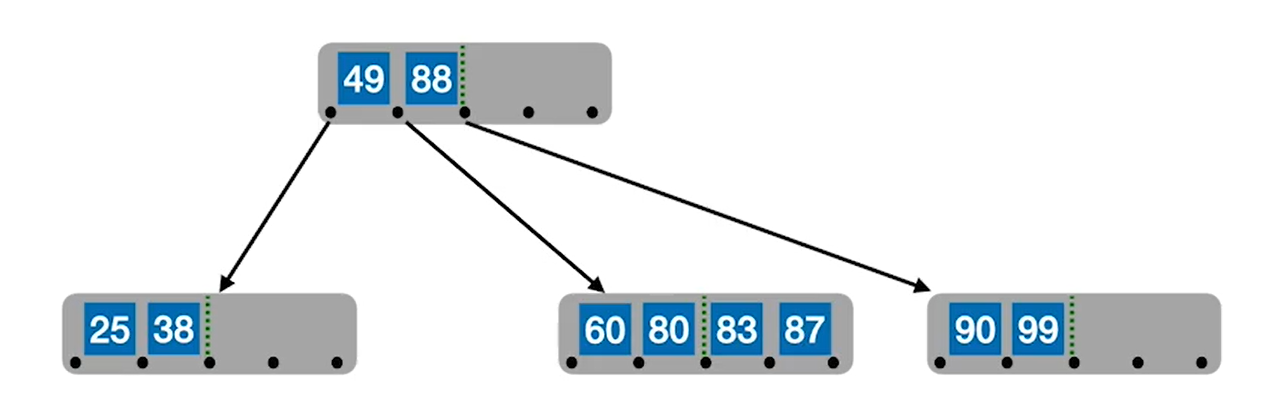
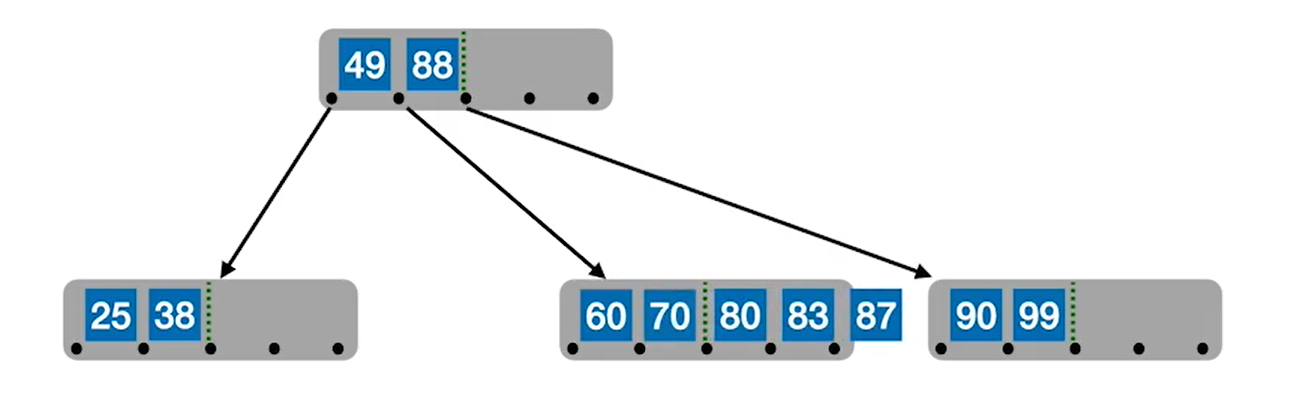
直接放入后，发现有个结点有五个元素，不满足五阶B树的性质，所以要将结点中位于中间的元素80提到父节点中，同时将结点分裂成两个结点以满足B树的性质。

 

 

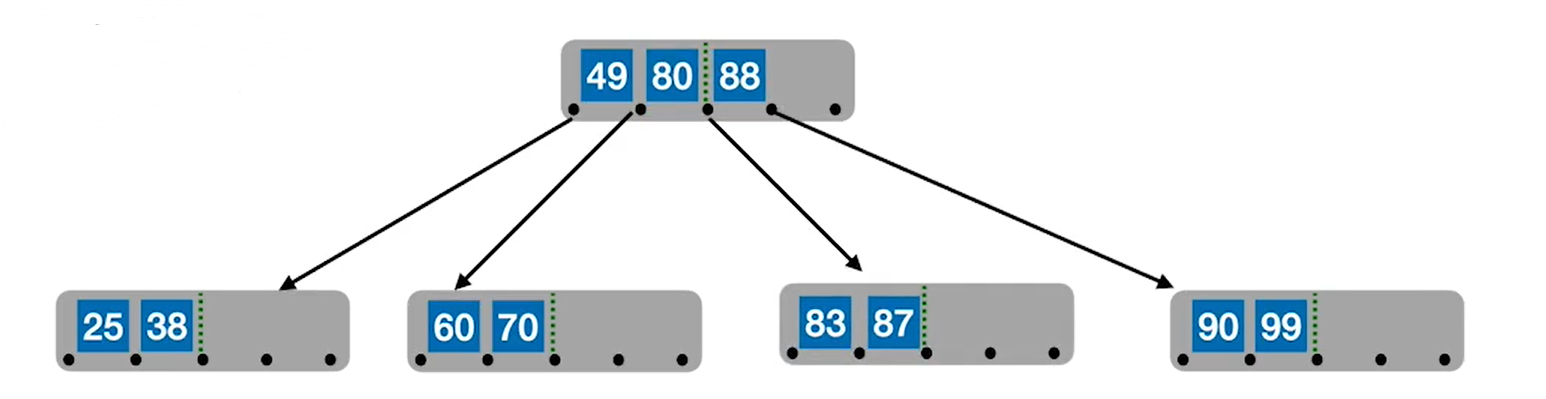
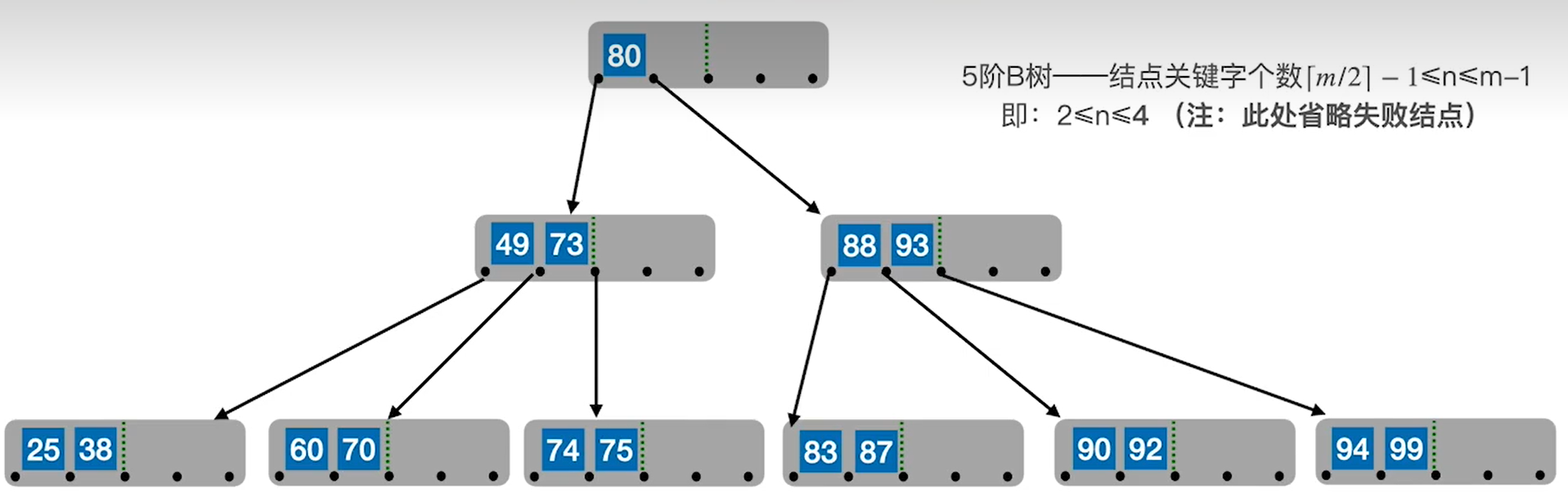
我们接续往其中添加元素后

 

 同理还可以将元素过多的结点取中位数放到父结点中。什么你说没有父结点怎么办，那就创造一个呗。创造的结点为根节点比较特殊，可以只拥有一个元素。

 

 

• 删除

 

对于这样一棵B树，现在准备删除元素60。

 

 

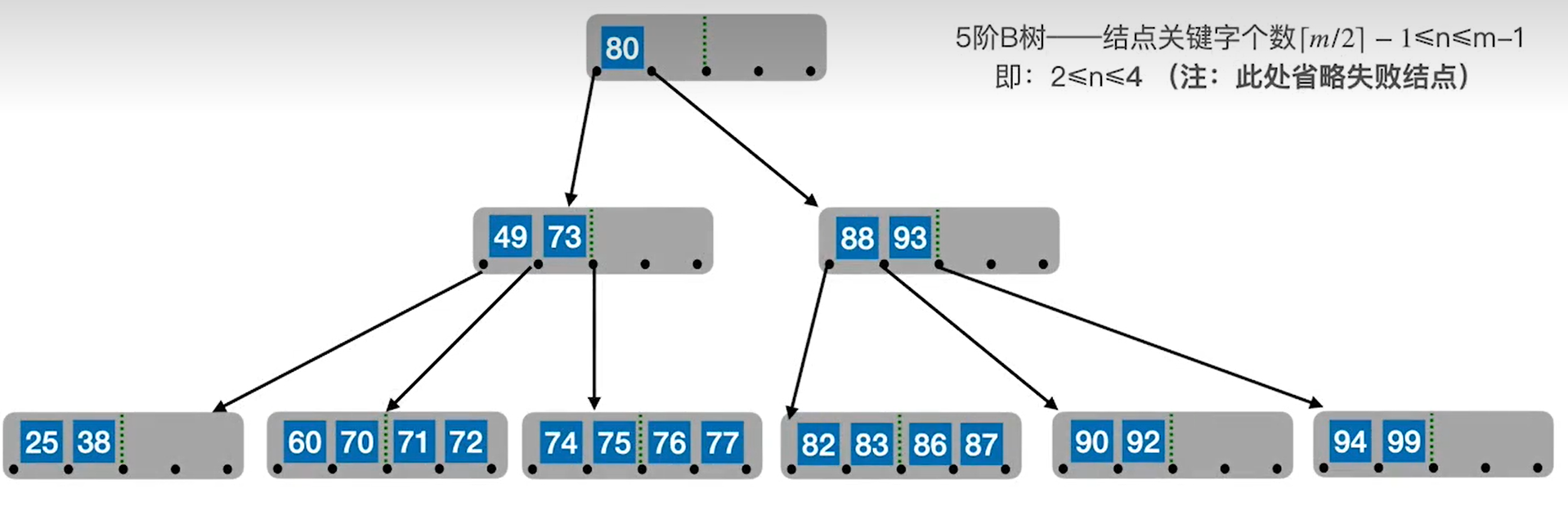
可以看出直接删除60后结点依旧拥有三个关键字是合法的，因此可以直接删除。

 

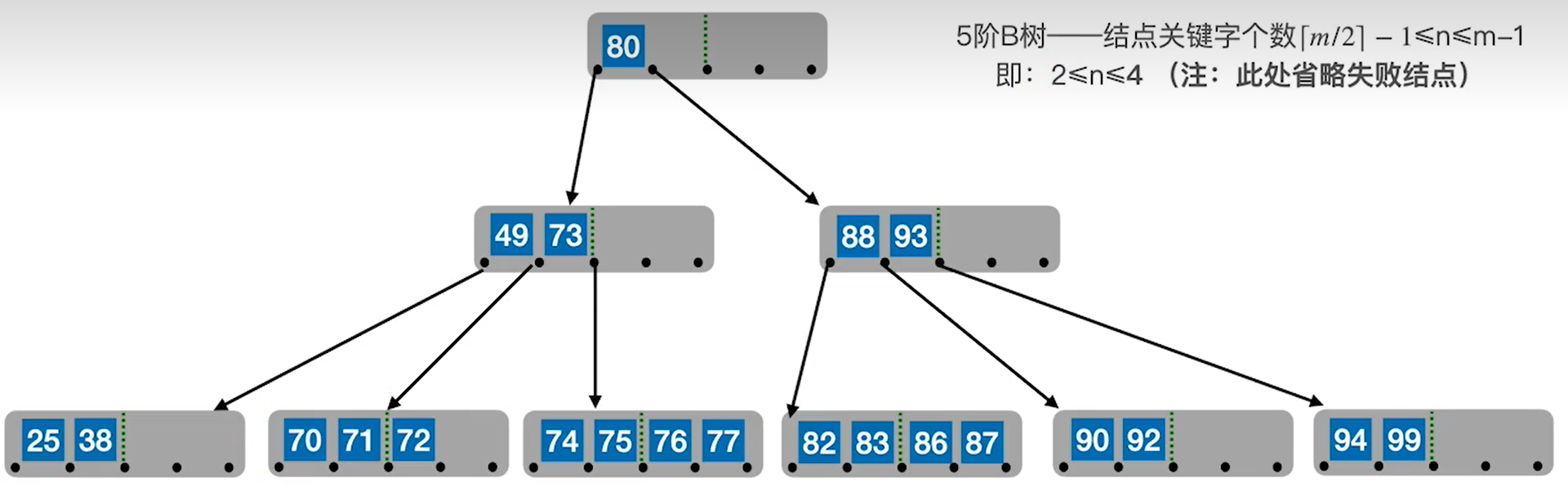
现在我们加大难度，准备直接把B树的根结点80给删了。

 

 

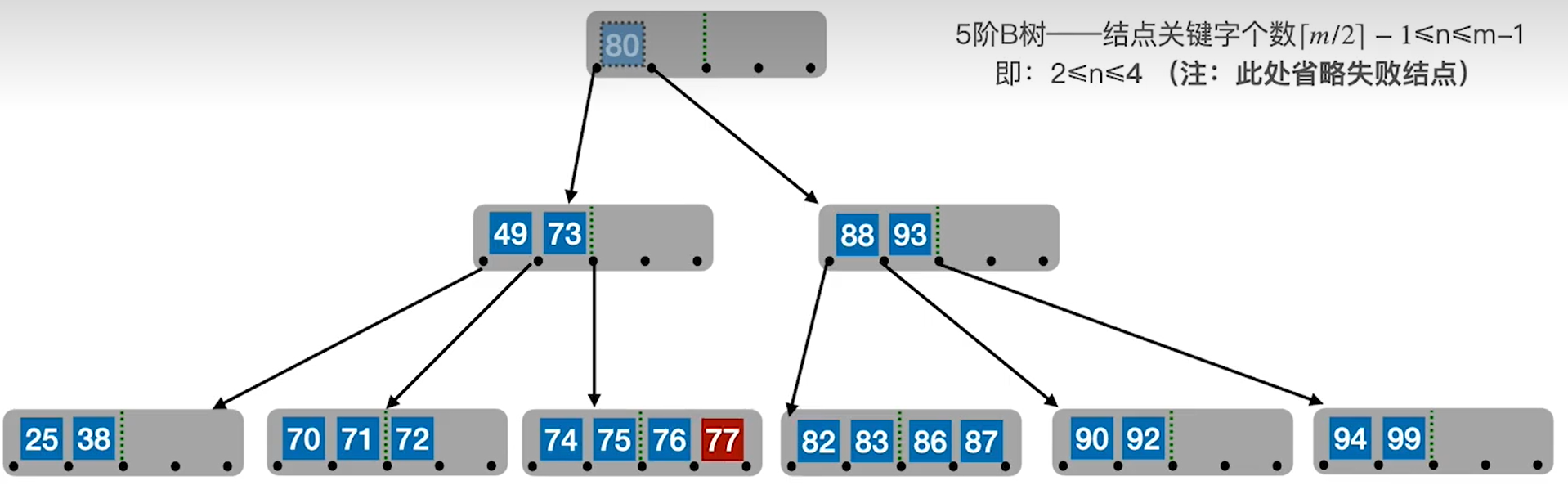
这时候其实有两种方法来完成删除操作，但其实大同小异。

若被删除关键字在非终端节点，则用直接前驱或直接后继来替代被删除的关键字。

 比如80的直接前驱是77，因为将B树中所有元素排序后，77是80的上一个数。同理80的下一个数是82，所以直接后继是82。77和82都能用来替代80。这里用77来替代。

 

 

 

 

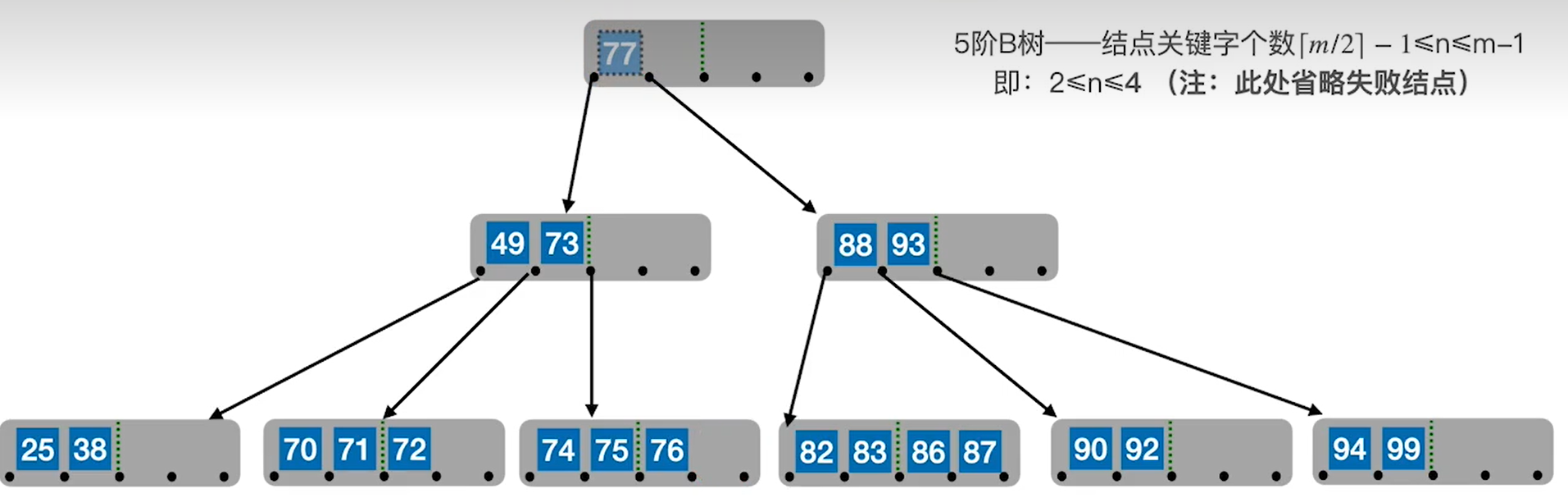
 继续删除77，用82来替代。

 

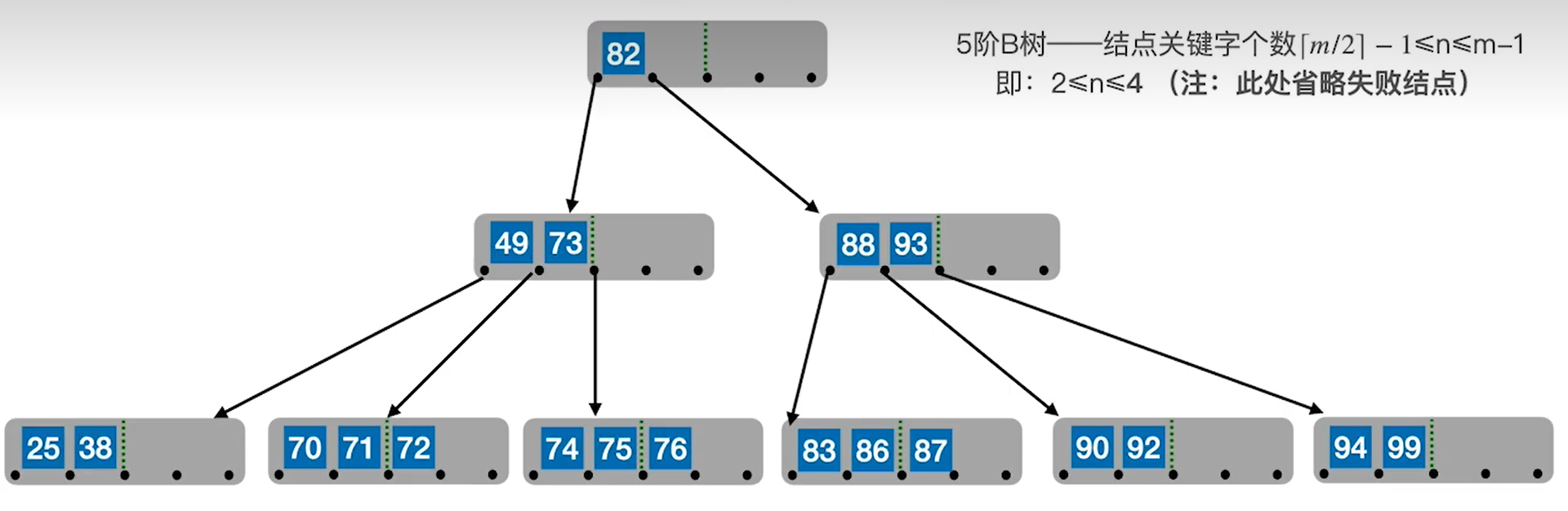
现在考虑删除后结点个数不足的情况，比如现在准备删除38，删除后结点只有25一个元素不满足二叉树的性质。

 

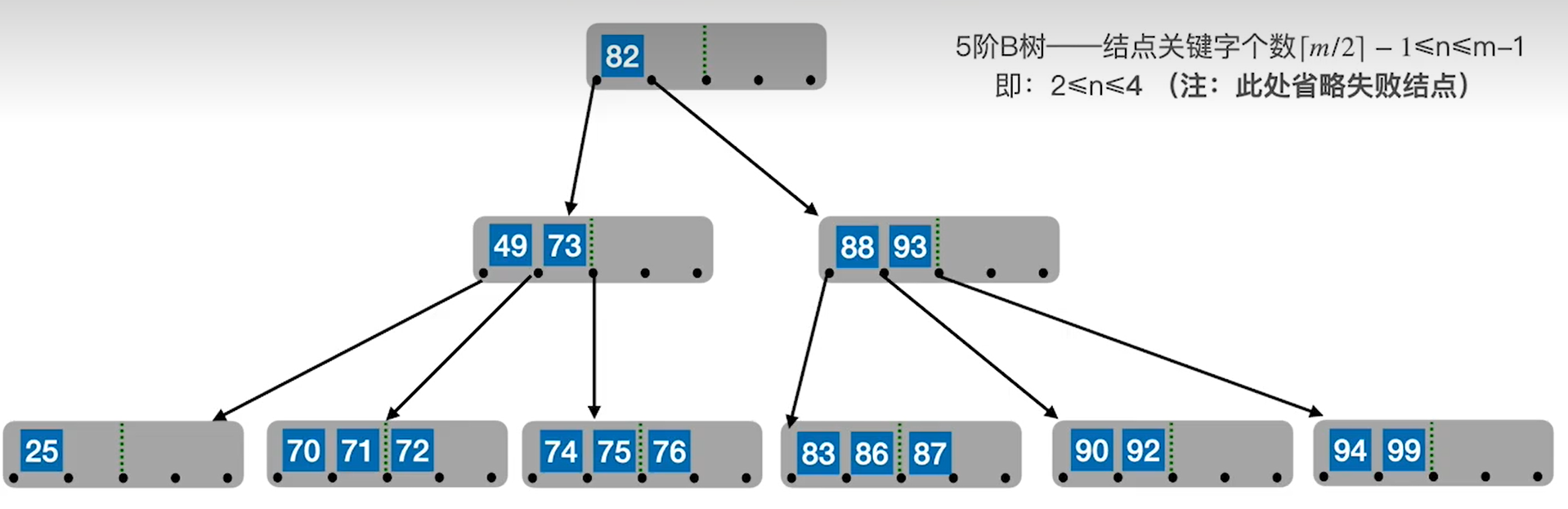
 这时候可以使用父子换位法，即将删除节点的后继替换当前结点，之后用删除结点后继的后继替换删除结点的后继。

对于这道题就是用49来替代删除的38，用70来替代49。这样相当于从父结点拿了个元素父结点又从兄弟结点拿了个元素，所以叫父子换位法。

 

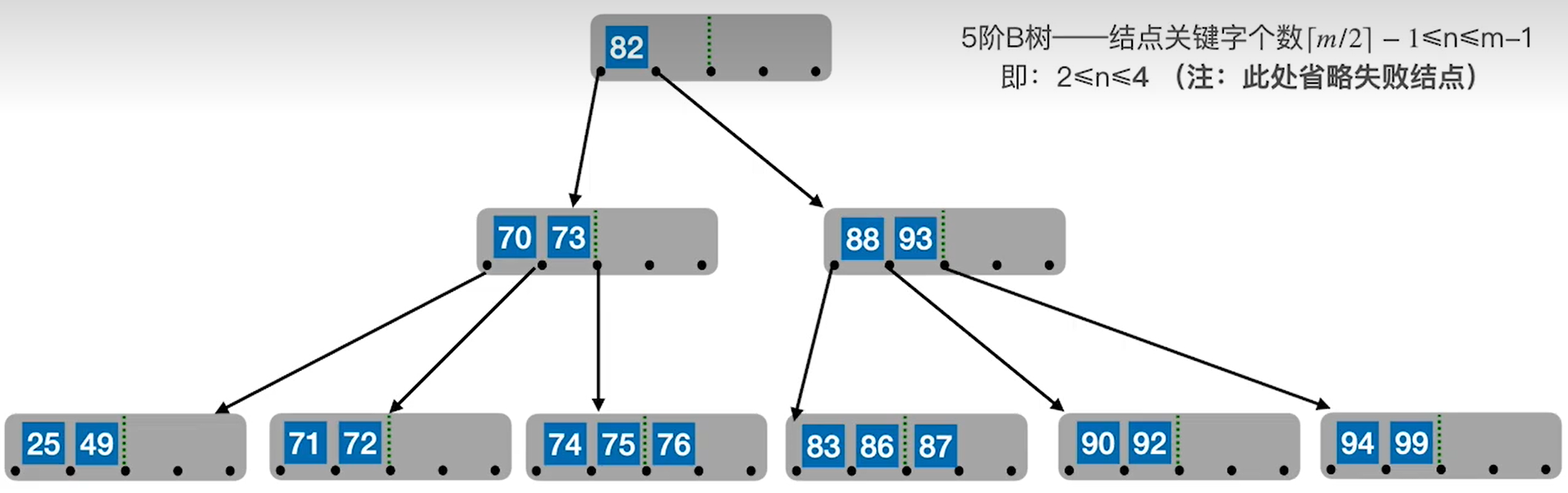
以此类推，如果删除的结点靠右边，则可以用前驱和前驱的前驱来替换。

 若删除后兄弟结点都不够借，则可以将两个兄弟结点合并。同时由于合并后父结点中用于区分两个兄弟的结点也没有用了，所以也要把父结点中的那个元素移动下来和两个兄弟结点一起合并。例如我们删除49之后合并。

 

 

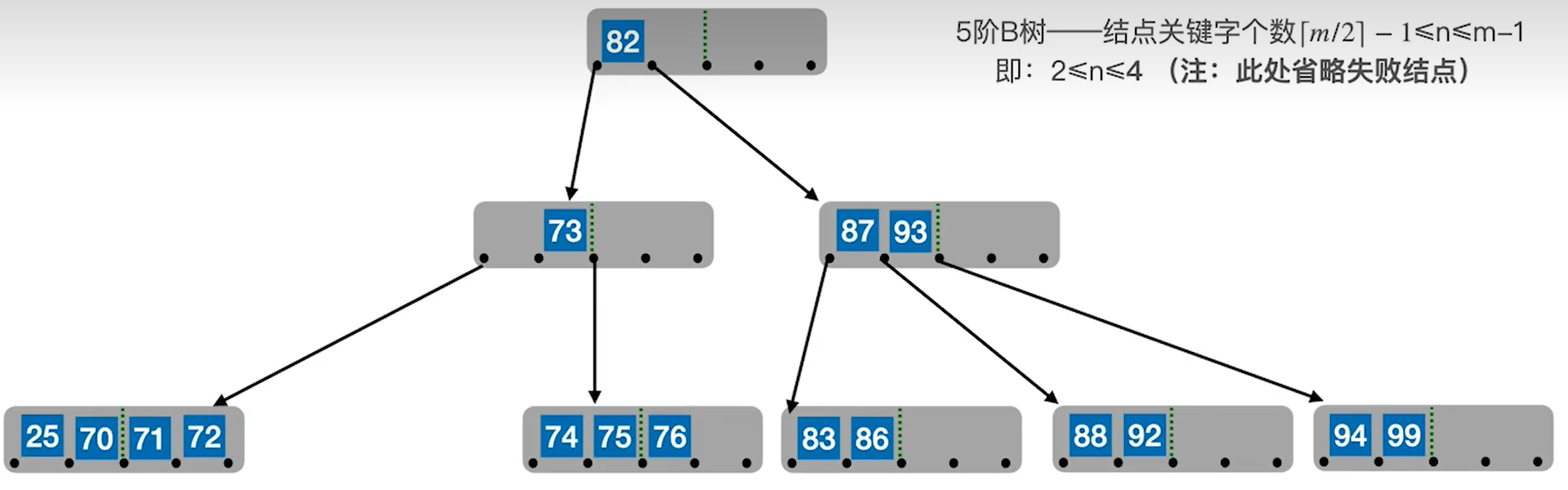
这时候中间的结点也不满足B树的性质，元素过少，也要继续合并。合并最后就如下图所示。

 

 

 

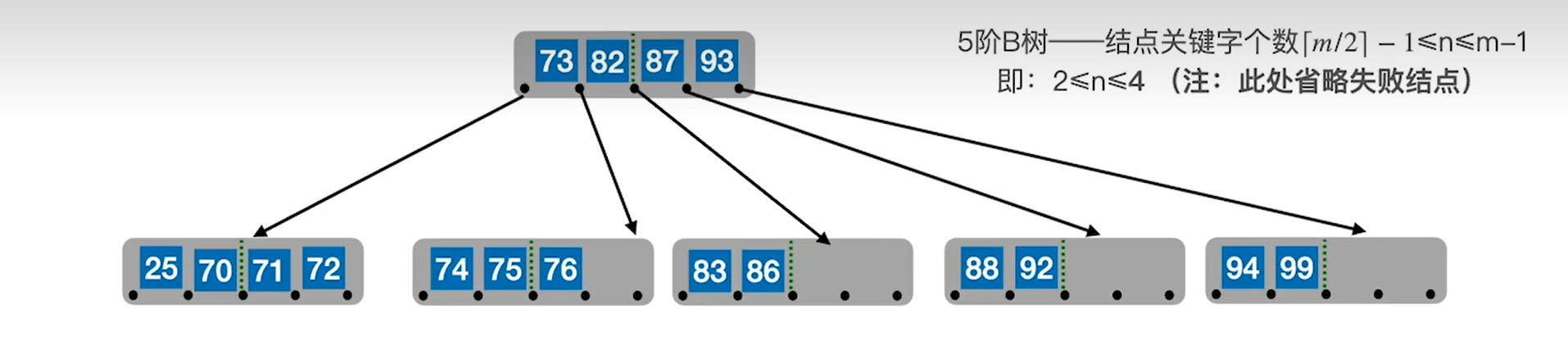
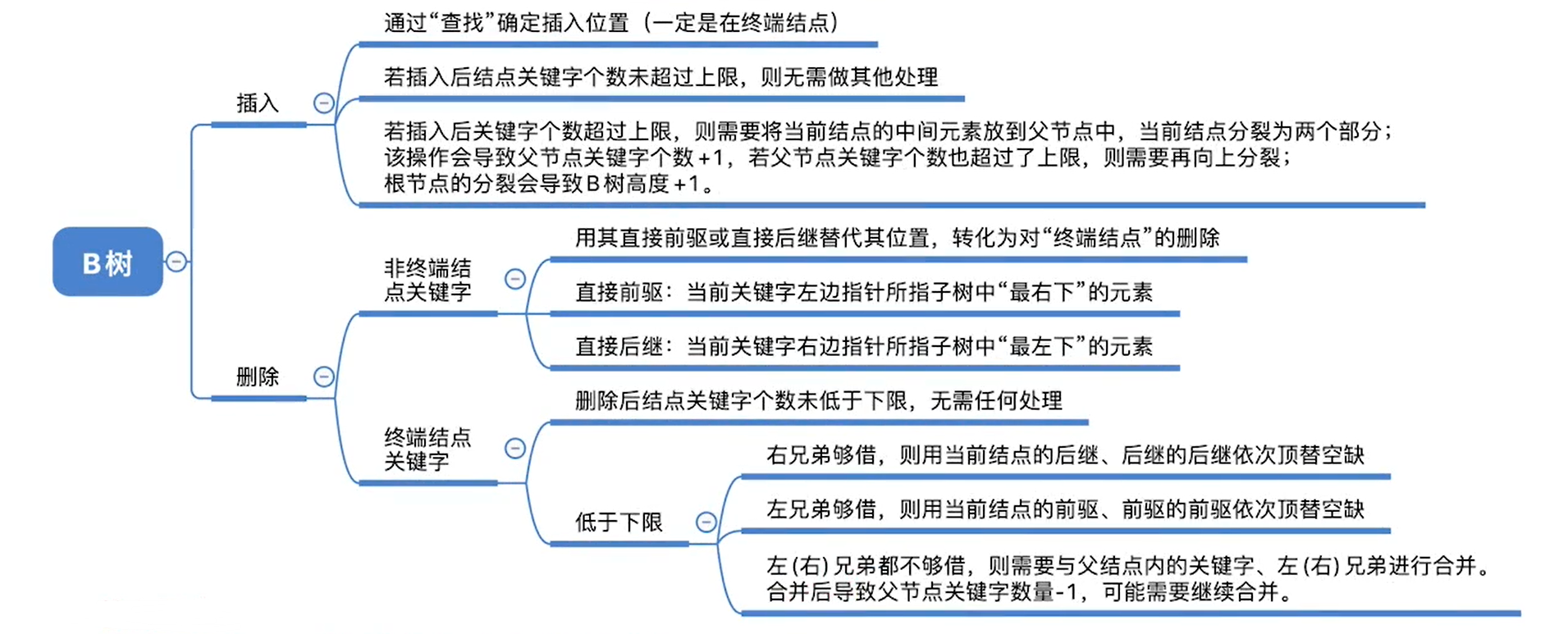
最后是一个总结，参考王道的课程。