题解：P3266 [JLOI2015] 骗我呢

题意

有一个 \(n \times m\) 的数组 \(x_{i,j} (1 \le i \le n, 1 \le j \le m)\)，满足：

• \(x_{i,j}\in[0,m]\)

• \(\forall i \in [1,n],\forall j\in[1,m),x_{i,j}<x_{i,j+1}\)

• \(\forall i \in (1,n],\forall j\in[1,m),x_{i,j} <x_{i-1,j+1}\)

求可能的数组 \(x_{i,j}\) 的解数，答案对 \(10^9+7\) 取模。

分析

首先根据 \(x_{i, j} < x_{i,j+1}\) 得到 \(i\) 相同的一行 \(m\) 个元素是单调上升的。

又因为 \(x_{i,j}\in[0,m]\)，所以这一行就是 \(0 \sim m\) 的序列中去掉一个元素。

---

考虑使用 dp。

令 \(dp_{i,j}\) 为第 \(i\) 行去掉元素 \(j\) 的解数。

模拟过程可得若第 \(i\) 行去除元素 \(j\)，那么第 \(i-1\) 行可以去除 \([0,j+1]\) 中的任一元素。

所以得到转移方程：

\[\begin{align} dp_{i,j}&=\sum^{j+1}_{k=0} dp_{i-1,k}\\ &=\sum^{j}_{k=0} dp_{i-1,k}+dp_{i-1, j+1} \\ &=dp_{i, j-1}+dp_{i-1,j+1} \end{align} \]

答案即为 \(\sum^m_{k=0}\limits dp_{n,k}=dp_{n+1,m-1}\)。

转移过程如下（\(n=3,m=4\)）：

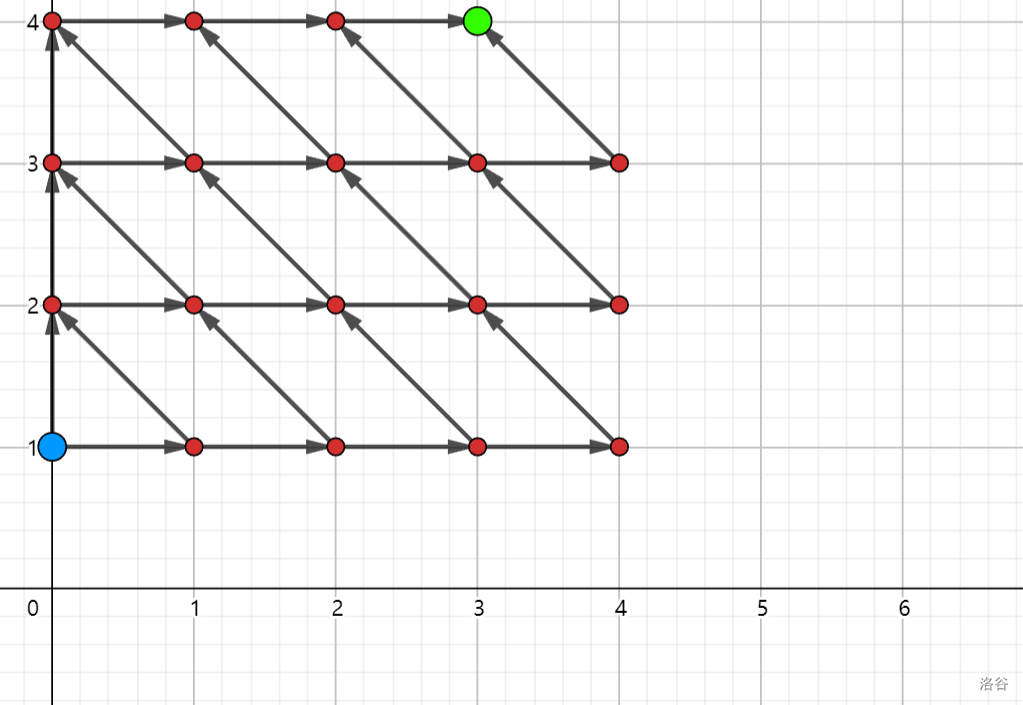
我们将这个图像拉伸，平移一下：

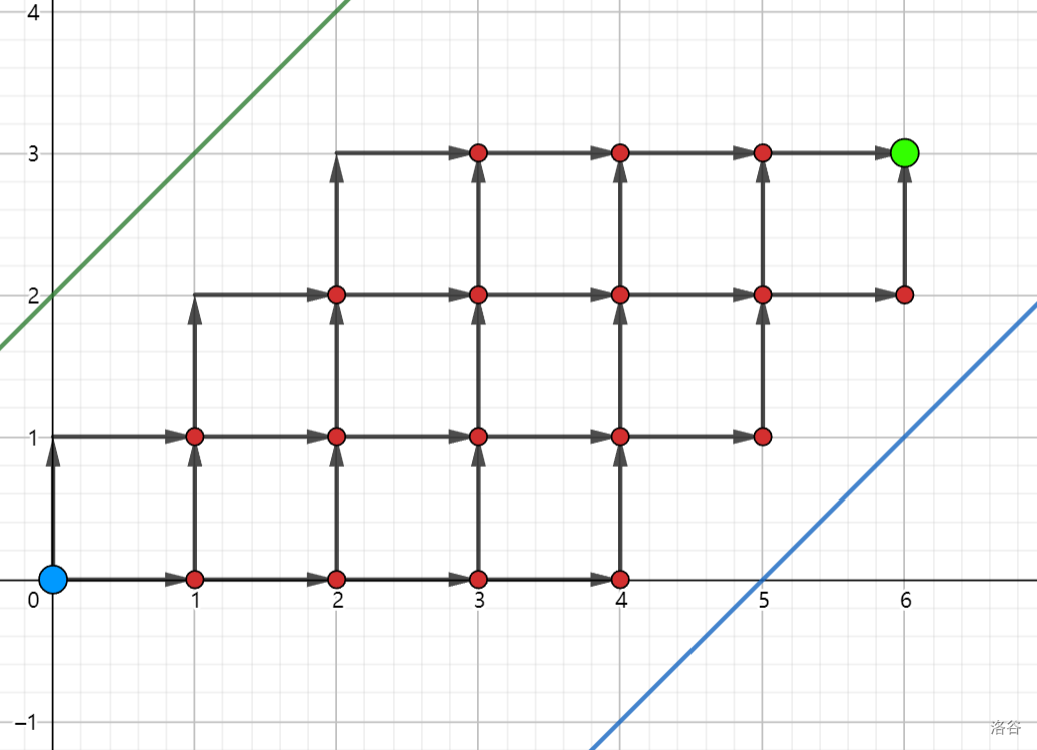
发现就是求从 \((0,0)\) 到 \((n+m-1,n)\) 且只能向上和向右且与直线 \(l_1:y=x+2\) 和直线 \(l_2:y=x-m-1\) 不交的路径数。

---

考虑使用反射容斥。

由容斥得：答案为总方案数 - 经过 \(l_1\) - 经过 \(l_2\) + 经过 \(l_1l_2\) + 经过 \(l_2l_1\) - 经过 \(l_1l_2l_1\) - 经过 \(l_2l_1l_2\)...

考虑如何计算每一部分。

已知从点 \((0,0)\) 到 \((n, m)\) 只能向上和向右的路径数为 \(\binom{n+m}{n}\)。

总方案数为原点到到 \((n+m-1,n)\) 的方案数。

经过 \(l_1\) 的方案数为原点到目标点 \(A\) 沿 \(l_1\) 对称得到的 \(A'\) 的方案数。

经过 \(l_1l_2\) 的方案数如何求解？

\(l_1\) 沿 \(l_2\) 对称得到直线 \(l_1'\)。

将 \(A'\) 沿 \(l_1'\) 对称得到 \(A''\)。

方案数即为原点到 \(A''\) 的方案数。

---

若某次对称得到的点 \(A_x\) 不在第一象限，那么结束循环。

Code

#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
#define maxn 4000006

int pre[maxn], inv[maxn];
int64_t ksm(int64_t x, int l)
{
    int64_t ret=1;
    for(;l;l>>=1, x=x*x%mod)
        if(l&1) ret=ret*x%mod;
    return ret;
}

int C(int n, int m) {return ((int64_t)pre[n]*inv[n-m]%mod)*inv[m]%mod;}

typedef pair<int, int> pos_t;
int path_count(pos_t p) {return C(p.first+p.second, p.first);}
pos_t reflect(int a, pos_t p) {return {p.second-a, a+p.first};}
int reflect(int a, int b) {return (a<<1)-b;}

int main()
{
    pre[0]=1;
    for(int i=1;i<maxn;i++) pre[i]=(int64_t)pre[i-1]*i%mod;
    inv[maxn-1]=ksm(pre[maxn-1], mod-2);
    for(int i=maxn-2;~i;i--) inv[i]=(int64_t)inv[i+1]*(i+1)%mod;
    int n, m;
    cin>>n>>m;
    int a1=2, a2=-m-1;
    int mul=-1, ans=path_count({n+m-1, n});
    for(pos_t p=reflect(a1, {n+m-1, n});p.first>=0&&p.second>=0;)
    {
        ans=((ans+mul*path_count(p))%mod+mod)%mod;
        a2=reflect(a1, a2);
        swap(a1, a2);
        p=reflect(a1, p);
        mul*=-1;
    }
    mul=-1;
    a1=-m-1, a2=2;
    for(pos_t p=reflect(a1, {n+m-1, n});p.first>=0&&p.second>=0;)
    {
        ans=((ans+mul*path_count(p))%mod+mod)%mod;
        a2=reflect(a1, a2);
        swap(a1, a2);
        p=reflect(a1, p);
        mul*=-1;
    }
    cout<<ans;
}