树状数组(Index Tree) 计算LIS 举例--java实现

举例

计算LIS.给定序列:2 5 3 7 3 1 9

步骤

根据给定序列个数,初始化树状数组.

给定的元素需要在二叉树的叶子节点上放置.所以树状数组的叶子节点必须不少于元素个数.
因为是二叉树,所以树状数组的大小必须是2^k.所以最终初始化大小的时候,只要选择第一个比
序列长度大的2^k即可.

树状数组是这样的:

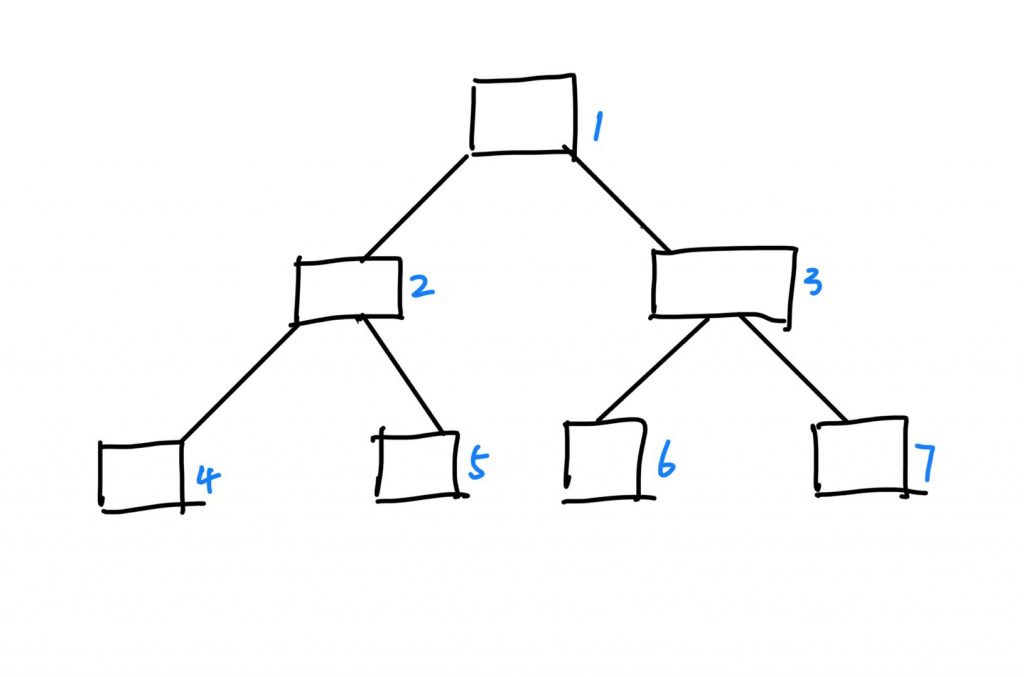
使用1节点的值表示4~7范围的值
使用2节点的值表示4~5范围的值
使用3节点的值表示6~7范围的值

如果要得到5_{7的值,需要5本身的值+6}7(也就是3)的值
获取值应该就是以上几种情况

对序列进行排序.

最长上升排序规则:     根据元素从小到大(因为要递增),如果元素相同,索引大的在前面(因为是严格递增)
最长不下降排序规则: 根据元素从小到大(因为要递增),如果元素相同,索引小的在前面(因为是不严格递增)

最长下降排序规则:     根据元素从大到小(因为要递减),如果元素相同,索引大的在前面(因为是严格递减)
最长不上升序规则:     根据元素从大到小(因为要递减),如果元素相同,索引小的在前面(因为是不严格递减)

根据排序后的序列,按照顺序放入树状数组中.

在往树状数组中放置的时候,由两个操作.

a.查询在当前位置之前,有几个比当前放置的值要大的元素的个数---query(fromIdx,toIdx)
b.更新当前位置的值,直到当前位置,最长 上升子序列的长度---update(index,value)

画图举例

首先将给定序列进行排序

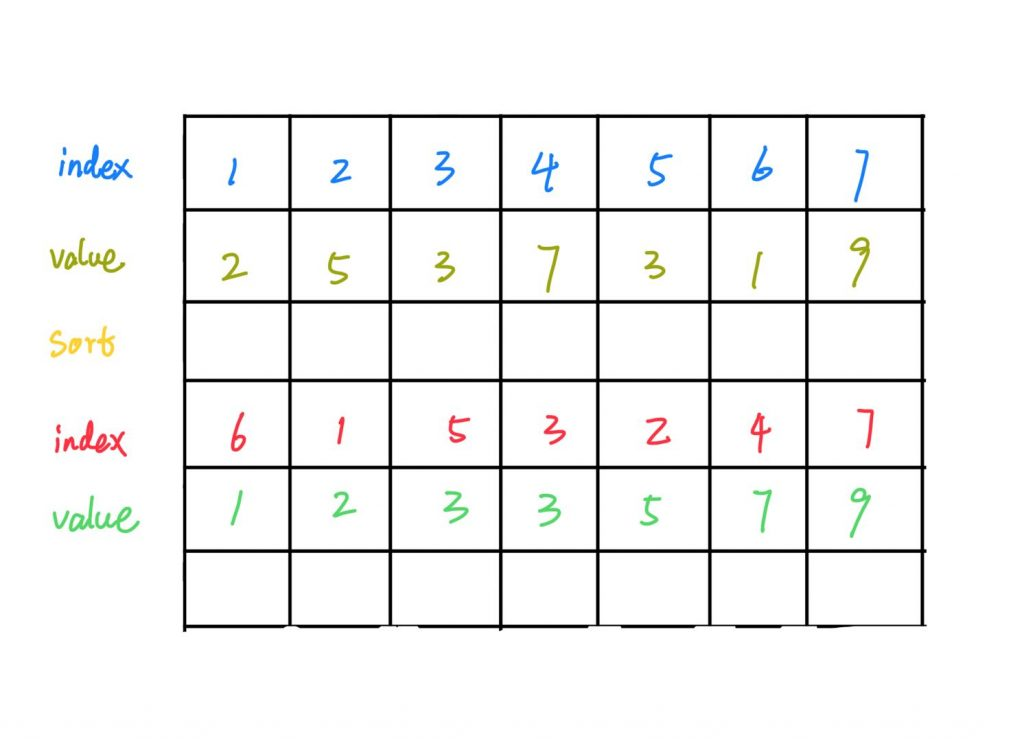
第一行和第二行代表原始序列的索引和值,sort后的两行代表排序后的索引和值.
可以看到,关于相同的3,index大的排列到前面,index小的排列到后面.
然后将它们放入树状数组中.

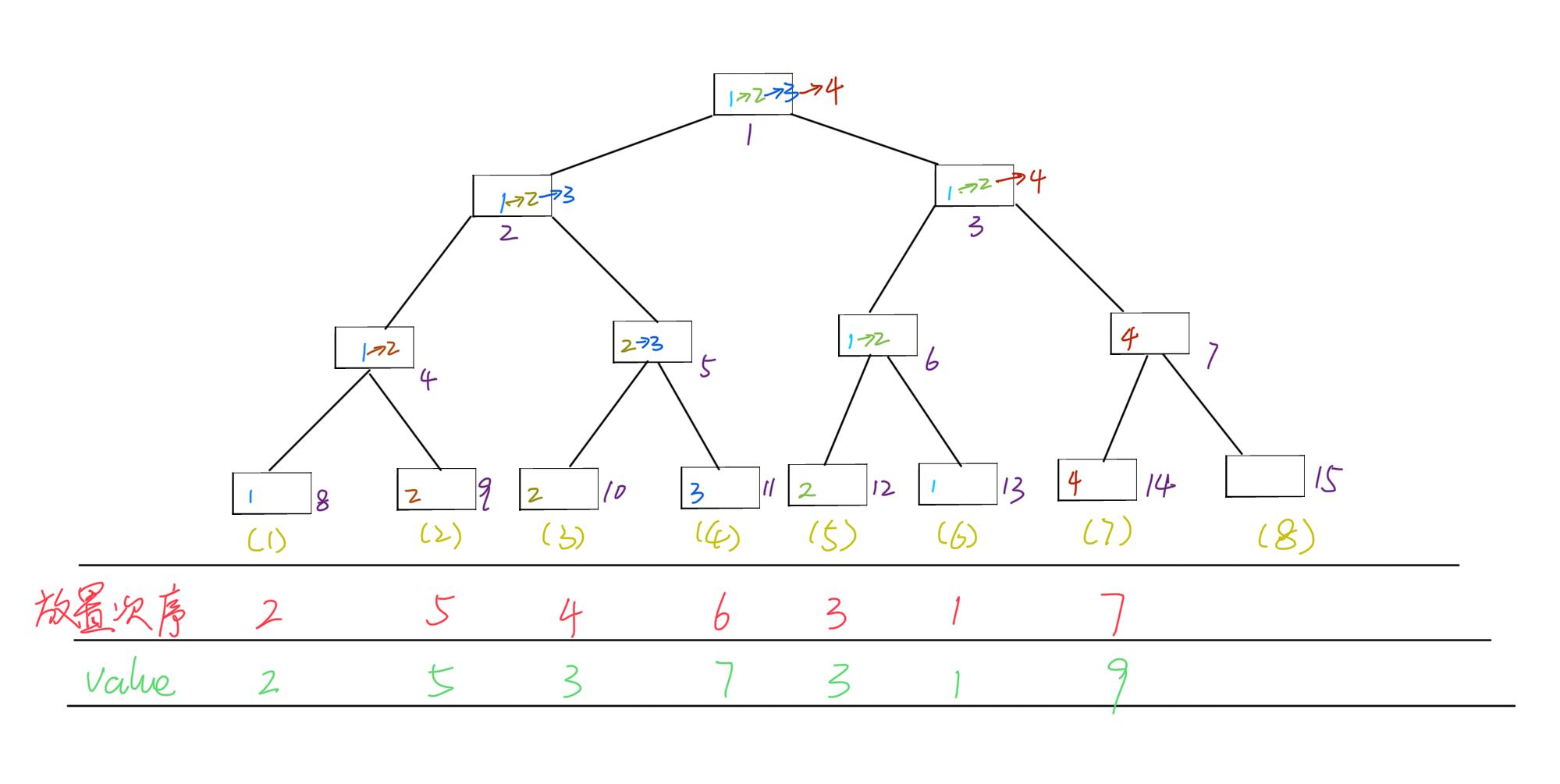
(不要在意很丑的文字...)
我这里按照不同颜色来表示不同的放置.颜色相同的箭头代表了树状数组被哪一次放置更新了.(实际上我不会做动态播放的图片 :weiqv: )
放置次序就是根据上面的排序后数组放置的.(这里就根据红色字,放置次序来看放的顺序吧)
a.放1的时候(放置次序1),在13号格子,前面都未放置其它值,所以13,6,3,1都被更新为1.
b.放2的时候(放置次序2),在8号格子,前面的格子都没有放置其它值(实际上也没有前面的节点了,它是第一个).所以8,4,2被更新为1.因为1号格子本身就是1,本次更新的值,没有比1格子的值大,所以不更新.
c.放3的时候(放置次序3),在12号格子(这时候按照索引从大到小排序就有用了),因为12号格子之前8号格子已经放了1,这代表我放它的时候,前面有一个数字比我小,于是当前的12号格子,需要放2(算上我本身,上升序列长度就是2了).于是6号节点需要从1变为2. 3,1节点也被更新为2.
d.放3的时候(放置次序4),在10号格子.和c一样,因为10号格子之前8号格子放了1,所以10号格子需要放2,依次更新父节点,均变为2.
e.放5的时候(放置次序5),在9号格子.仍然和c一样,将9号格子值变为2,同时更新父节点4号格子.因为2号格子值本身就是2,所以不需要更新.
f.放7的时候(放置次序6),在11号格子.因为11号之前8,9,10都放了数值,我们需要在它们最大的基础上增加1,表示最大序列增加了一个.所以需要放3.同时更新所有父节点.
g.放9的时候(放置次序7),在14号格子,和f一样,查询出8~13号格子的数值的最大值,在此基础上增加1表示最大序列增加了一个.所以需要放置4.同时更新所有父节点.

h.现在放置完毕,我们要找例子中数组的最长上升序列,只需要去查找1号格子值就可以啦.答案为4. :taikaixin:
根据步骤描述,就需要之前说的query和update方法了.
query方法查询当前位置之前的范围区间的值(这里是查找最大值,也可以用于其它的区间相关的统计),update方法用来更新本身和父节点的值.

根据一道模板题目,加深对它的理解吧.主要就是树状数组关键的两个方法.(POJ3903)

Stock Exchange
Time Limit: 1000MS

Total Submissions: 11485

Description

The world financial crisis is quite a subject. Some people are more relaxed while others are quite anxious. John is one of them. He is very concerned about the evolution of the stock exchange. He follows stock prices every day looking for rising trends. Given a sequence of numbers p1, p2,...,pn representing stock prices, a rising trend is a subsequence pi1 < pi2 < ... < pik, with i1 < i2 < ... < ik. John’s problem is to find very quickly the longest rising trend.

Input

Each data set in the file stands for a particular set of stock prices. A data set starts with the length L (L ≤ 100000) of the sequence of numbers, followed by the numbers (a number fits a long integer).
White spaces can occur freely in the input. The input data are correct and terminate with an end of file.

Output

The program prints the length of the longest rising trend.
For each set of data the program prints the result to the standard output from the beginning of a line.

Sample Input

6
5 2 1 4 5 3
3
1 1 1
4
4 3 2 1

Sample Output

3
1
1

Hint

There are three data sets. In the first case, the length L of the sequence is 6. The sequence is 5, 2, 1, 4, 5, 3. The result for the data set is the length of the longest rising trend: 3.

Source

Southeastern European Regional Programming Contest 2008

以下是代码:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
import java.util.StringTokenizer;

public class Main {
   static int n,len;
   static int[] lis;
   public static void main(String[] args) throws Exception {
       Scanner sc = new Scanner(System.in);
       while (sc.hasNextInt()){
           n = sc.nextInt();
           len = 1;
           while (len<n){
               len*=2;
           }
           lis = new int[len*2];
           int[][] data = new int[n][2];
           for(int i = 0;i<n;i++){
               data[i] = new int[]{sc.nextInt(),i};
           }
           Arrays.sort(data, new Comparator<int[]>() {
               @Override
               public int compare(int[] o1, int[] o2) {
                   if(o1[0] == o2[0]){
                       return o2[1]-o1[1];
                   }
                   return o1[0]-o2[0];
               }
           });
           for(int[] s:data){
               int preCnt = query(len,len+s[1]-1);
               update(s[1]+len,preCnt+1);
           }
           System.out.println(query(len,len+n-1));
       }
   }

   private static int query(int start,int end){
       int result = 0;
       while (start<=end){
           if(start%2 == 1){
               result = Math.max(lis[start],result);
           }
           if(end%2 == 0){
               result = Math.max(lis[end],result);
           }
           start = (start+1)/2;
           end = (end-1)/2;
       }
       return result;
   }
   private static void update(int index,int val){
       while (index>0 && val>lis[index]){
           lis[index] = val;
           index/=2;
       }
   }
}