计算全为1的矩阵数量 java实现

题目链接:SQUARE

这种类型题目算是模板题目吧...poj,洛谷,leetcode都有.

可以使用压缩矩阵和动态规划两种方式求解.不过动态规划计算正方形还行,如果计算矩形的话,可能还要再给dp数组增加一维.

一 动态规划

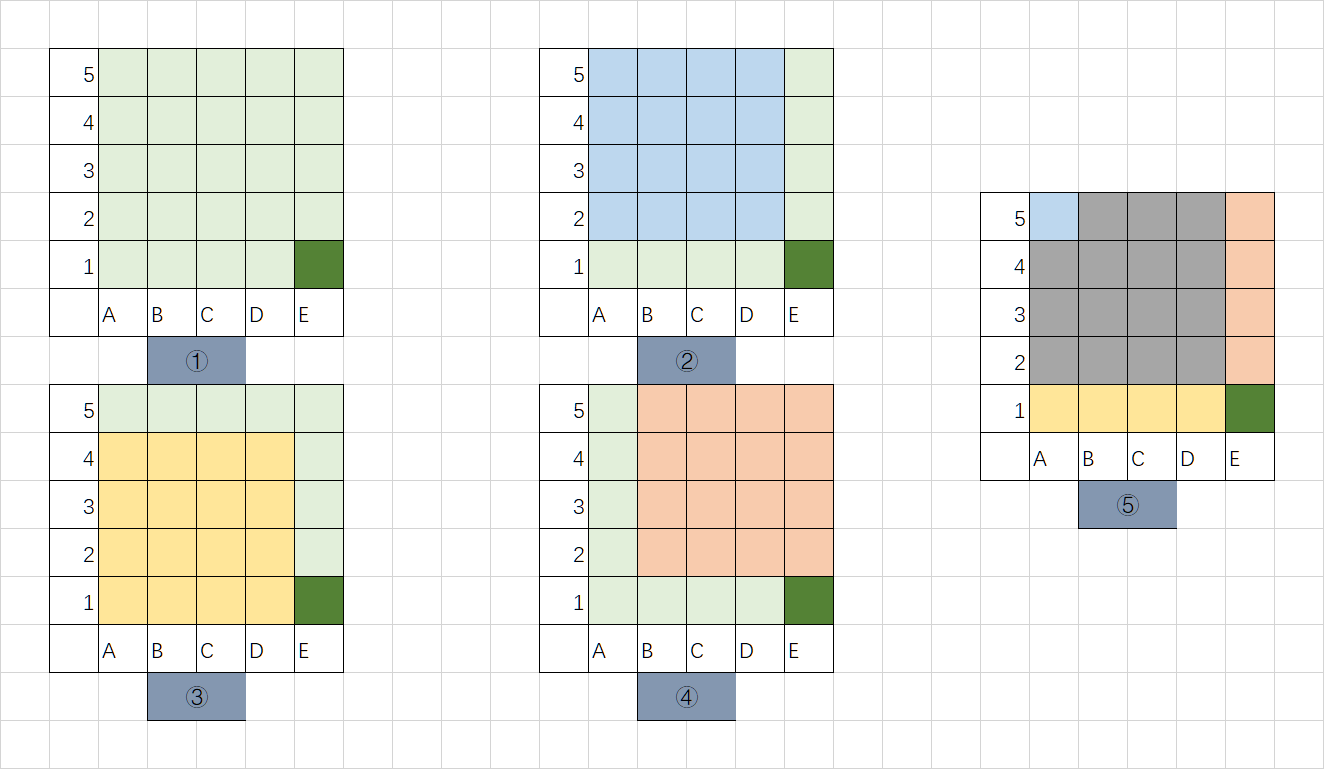
对于动态规划,只说一下计算正方形的情况.想一下这张图片:

对于右下角的E1,以它为终点,长度为5的正方形(①)是否存在,可以通过以它右上角为顶点的正方形(②),以它左边方格为顶点的正方形(③)和以它上方方格为顶点的正方形(④)来一起判断.

查看⑤.②,③,④确定的颜色都涂在了⑤上,灰色是共同部分.

所以可以写出状态转移方程了.

设动态规划数组为dp[N][N][N],其中N为矩阵长度.元素dp[i][j][k]含义是以坐标为(i,j)的元素为右下角,边长为k的正方形是否存在.存在为1,不存在为0.

于是:dp[i][j][k] = dp[i-1][j][k-1]dp[i][j-1][k-1]dp[i-1][j-1][k-1]==1?1:0

dp中使用第三维宽度可以灵活地计算出宽度为k地子正方形个数.最终只要遍历dp数组求和就可以了.

以下是代码:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
 
/**
 * 动态规划
 */
public class source {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int[][] info = new int[N][N];
 
        int dp[][][] = new int[N][N][N];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                info[i][j] = Integer.parseInt(st.nextToken());
                if (info[i][j] == 1) {
                    dp[i][j][0] = 1;
                } else {
                    dp[i][j][0] = 0;
                }
            }
        }
        int cnt=0;
        for (int i = 1; i < N; i++) {
            for (int j = 1; j < N; j++) {
                for (int k = 1; k < N; k++) {
                    if(info[i][j] == 1){
                        if (dp[i][j - 1][k - 1]*dp[i - 1][j][k - 1]*dp[i - 1][j - 1][k - 1] != 0) {
                            dp[i][j][k] = 1;
                            cnt++;
                        }
                    }
                }
            }
        }
 
        System.out.println(cnt);
    }
}

以下是运行结果:

Testcase	시간	메모리	결과
1	0.085 초	21327872 byte	맞았습니다
2	0.088 초	25128960 byte	맞았습니다
3	0.152 초	26292224 byte	맞았습니다
4	0.141 초	27881472 byte	맞았습니다
5	0.464 초	140136448 byte	맞았습니다
6	0.476 초	140136448 byte	맞았습니다
7	0.503 초	140177408 byte	맞았습니다
8	0.51 초	140177408 byte	맞았습니다

二 压缩矩阵

这种方法除了计算正方形外,还可以计算矩形.

考虑这个图片:

按照箭头1~6顺序来看.

①是压缩前两个数组,通过与运算压缩过后,就能够得到新的数组[0,0,1,1,1,1].

因为是前两个进行的压缩,所以这个数组中的1的含义表示前两行里能够组成矩阵的1的位置.

所以数组中第三个位置表示使用前两行的话,第三列是能够构成矩形的.

因为这时候压缩的高度是2,所以三四,四五,五六位置合起来都是能够构成正方形的.

可以按照这个体会以下从上到下压缩的流程.

图片中将第一行作为起始位置进行了压缩,实际还需要从第二个位置开始一直到最后一个位置,都作为起始位置执行压缩操作,进行矩阵个数计算.

知道了能够构成矩阵的位置,知道了压缩的高度,这样就能计算出任意能够构成m*n矩形的个数了.

以下是java代码,这里计算的是至少为4个正方形所组成的大正方形个数.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
 
public class source {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int[][] info = new int[N][N];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                info[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        int res = 0;
        for (int k = 0; k < N; k++) {
            int[] tempArray = Arrays.copyOf(info[k], N);
            for (int i = k + 1; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    tempArray[j] = info[i][j] & tempArray[j];
                }
                res += calcCnt(tempArray, i - k + 1);
            }
        }
        System.out.println(res);
    }
 
    private static int calcCnt(int[] array, int height) {
        int cnt = 0;
        int res = 0;
        int temp = 0;
        for (int i = 0; i < array.length; i++) {
            if (array[i] == 1 && cnt <height) {
                cnt++;
            }
            if (array[i] == 0) {
                cnt = 0;
                temp = 0;
            }
            if(cnt == height){
                res++;
            }
 
        }
        return res;
    }
}

以下是运行结果:

Testcase	시간	메모리	결과
1	0.083 초	21065728 byte	맞았습니다
2	0.085 초	21065728 byte	맞았습니다
3	0.134 초	21590016 byte	맞았습니다
4	0.136 초	23687168 byte	맞았습니다
5	0.247 초	28680192 byte	맞았습니다
6	0.25 초	28680192 byte	맞았습니다
7	0.299 초	28680192 byte	맞았습니다
8	0.256 초	28680192 byte	맞았습니다

比较一下发下比上面的动态规划会快挺多的.