重建二叉树 java dfs实现

最近做了一个题:

重建二叉树

根据前序遍历+中序遍历得到树的后序遍历.

我是参考了LeetCode的解题做的.

按照题目的测试用例:

前序遍历:DBACEGF
中序遍历:ABCDEFG
需要输出后序遍历:ACBFGED

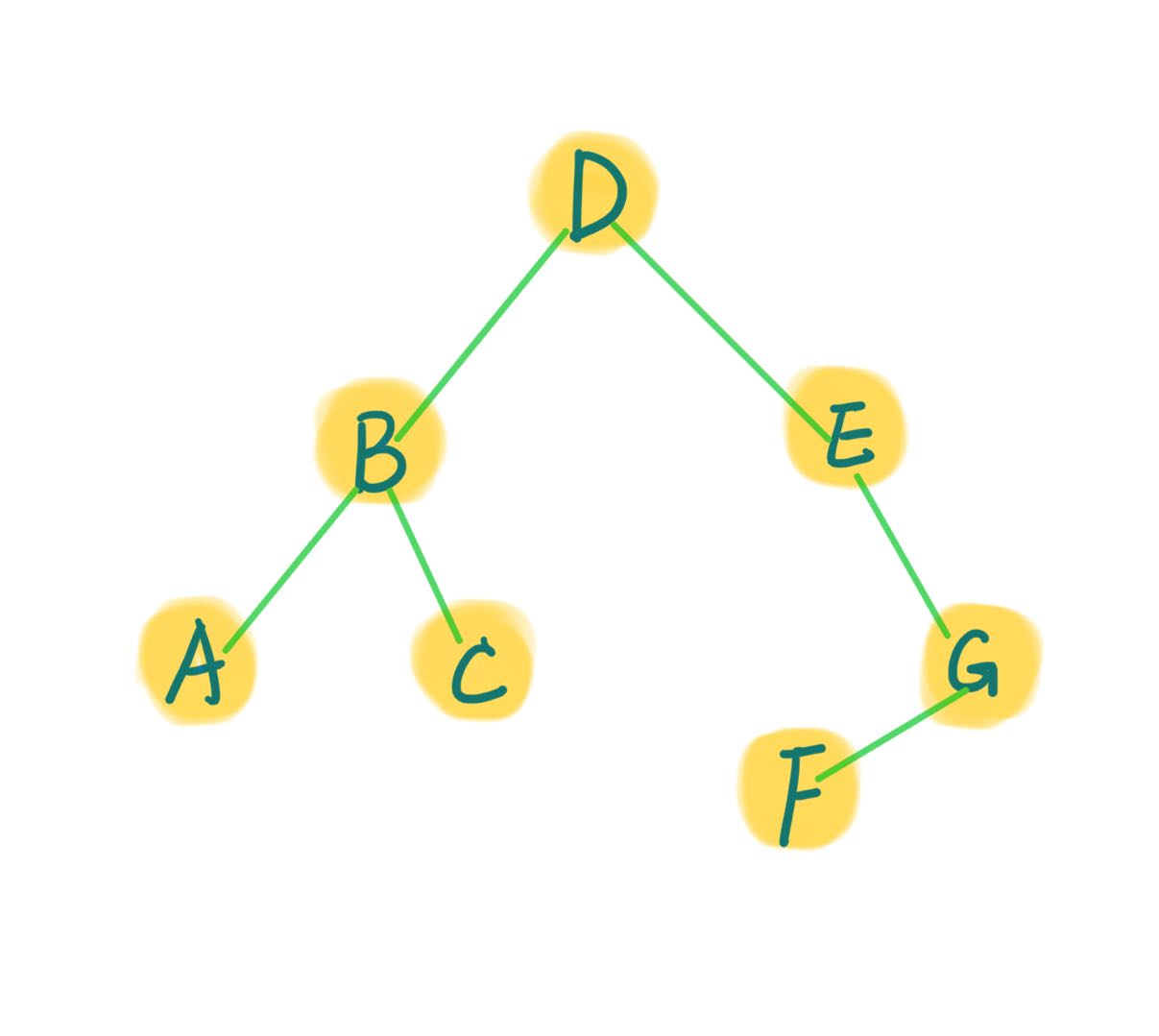
这是根据先序和中序遍历得到的二叉树.
先序遍历:先遍历root节点,再遍历左子树,最后遍历右子树
中序遍历:先遍历左子树节点,再遍root节点,最后遍历右子树
后序遍历:先遍历右子树,再遍历左子树,最后遍历root节点
所以:
1.先序遍历的第一个点一定是整个树的根.
2.在中序遍历中找到根节点所在的位置.这个位置的左半部分就是整个左子树的节点,右半部分就是右子树的节点.
3.区分了整个左子树和右子树后,根据子树再使用2的规则.
先序遍历的第二个节点是左子树的root节点,左子树的范围就是0~2中的root在中序遍历中所在的位置-1.
4.根据左子树的范围,在先序遍历中确定右子树root节点的位置.先序遍历需要root和左子树遍历完毕后,才能到右子树的根节点.
所以右子树root位置=root位置+左子树的长度+1.
5.对于下面的子树仍旧按照这个方式,将节点输出.
以下是java代码实现:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
static String s="";
static char[] pre;
static char[] mid;
static String[] split;
static Map<Character,Integer> value2Idx;
static List resultNodeNames;
public static void main(String[] args) throws Exception {

    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    while(!(s = br.readLine()).equals("")){
        value2Idx = new HashMap<>();
        if(s.length() == 1){
            System.out.println(s);
            continue;
        }
        split = s.split(" ");
        pre = split[0].toCharArray();
        mid = split[1].toCharArray();
        //将字符和它在中序遍历中的索引对应起来,后续dfs需要使用它来确定root位置,以及左右子树.
        for(int i =0;i<mid.length;i++){
            value2Idx.put(mid[i],i);
        }
        Node result = dfsNode(0,0,mid.length-1);
        resultNodeNames = new ArrayList<>();
        postGetNode(result);
        StringBuilder bu = new StringBuilder();
        for(Character c:resultNodeNames){
            bu.append(c);
        }
        System.out.println(bu.toString());
    }
}

/**
 *
 * @param preIdx root节点的位置
 * @param midLeftIdx 树的起始索引位置
 * @param midRightIdx 树的终止索引位置
 * @return Node root
 */
private static Node dfsNode(int preIdx,int midLeftIdx,int midRightIdx){
    if(midLeftIdx>midRightIdx){
        return null;
    }

    //root节点,根据先序遍历得到root节点本身名字
    Node root = new Node(pre[preIdx]);
    //root节点在中序遍历中的位置
    int rootIdx = value2Idx.get(pre[preIdx]);
    //root的left.左子树的root节点位preIdx+1,表明是先序遍历中root后面的一个元素
    //左子树的开始位置不变,终止位置变成了中序遍历中root索引位置的前一个位置,所以midRightIdx变成了rootIdx-1
    root.left = dfsNode(preIdx+1,midLeftIdx,rootIdx-1);
    //root的right.左子树的长度是上方的第二个参数-第一个参数+1:rootIdx-1-midLeftIdx+1.加上root本身所在的位置,的后续一位,便是右子树的root位置.
    //因为先序遍历的时候:root|左子树的root|左子树部分的所有节点|右子树的root.所以right的root索引preIdx = preIdx+(rootIdx-1-midLeftIdx+1)+1.
    //midRightIdx是不变的,作为右子树的结束位置.
    root.right = dfsNode(preIdx+(rootIdx-1-midLeftIdx+1)+1,rootIdx+1,midRightIdx);
    return root;
}

private static void postGetNode(Node node){
    if(node.left !=null){
        postGetNode(node.left);
    }
    if(node.right!=null){
        postGetNode(node.right);
    }
    resultNodeNames.add(node.value);
}

static class Node{
    char value;
    Node left;
    Node right;
    Node(char value){
        this.value = value;
    }
}

}

这里是二叉树的三种遍历方式