八皇后问题

题目链接:八皇后

这里先粘贴一下正经的解法的代码,使用的是递归.

(可能在canPut的判断上会有疑问,这里也粘贴一个自己画的图)

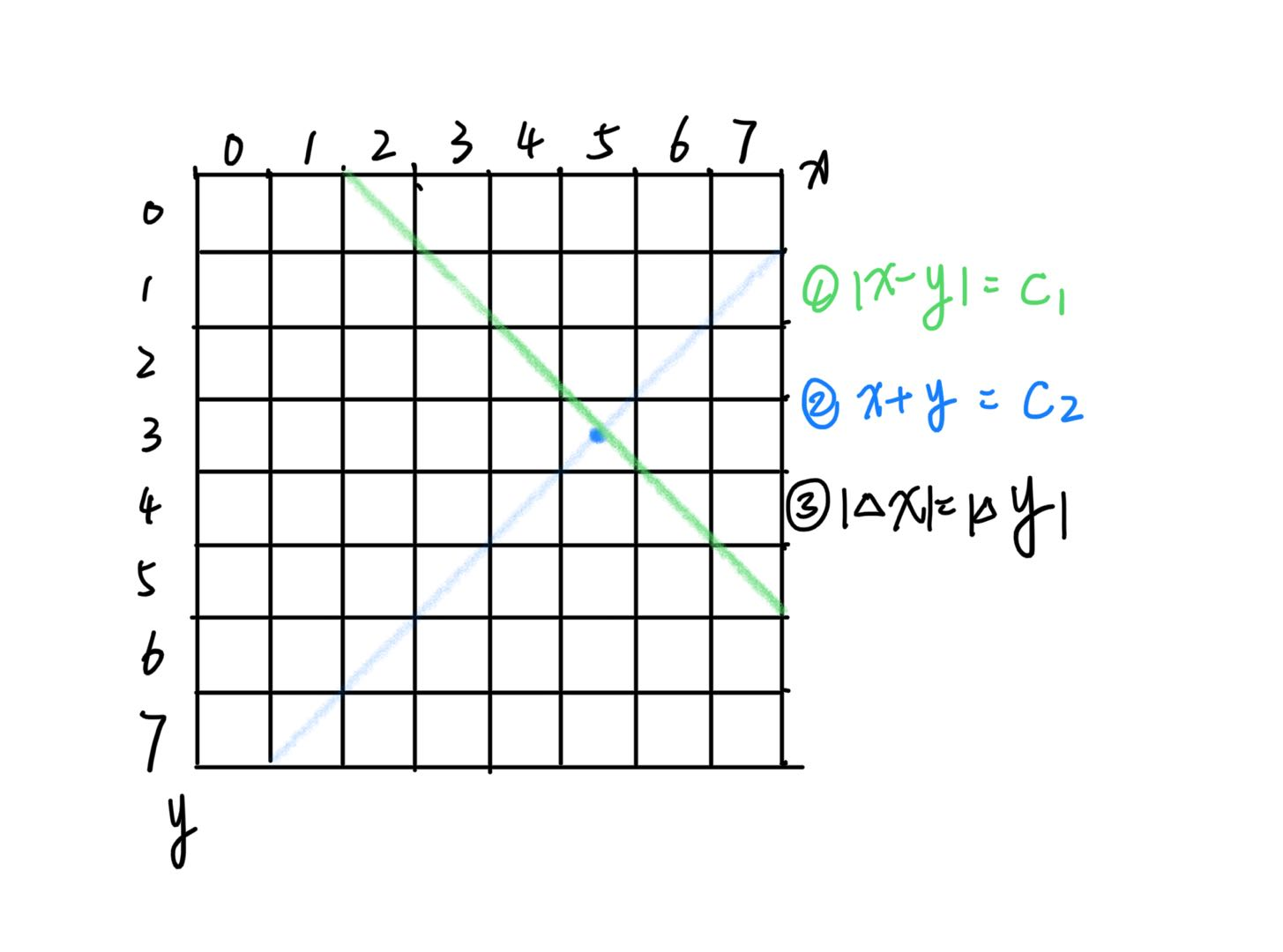
注释也说的听清楚的,就在配合图片解释一下为什么使用

Math.abs(row - i) == Math.abs(queues[row] - queues[i])
来判断对角线.
因为两条线斜率是±1,所以x方向和y方向变化率的绝对值是相等的.所以会有这个等式.
最终结果只需要输出ans这个list就可以了.
以下是代码:
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Main {
private static int[] queues;
private static List<List> ans = new ArrayList<>();

public static void main(String[] args) throws Exception {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    StringTokenizer st = new StringTokenizer(br.readLine());
    int n = Integer.parseInt(st.nextToken());
    queues = new int[n];
    traceBack(0,n);
}

/**
 * 计算当前行能否放置皇后,如果可以放置,就搜索下一行
 * 如果不能放置,就替换queues[i],替换第i行需要放置的位置.
 * 如果最后0~7都放完了,就记录放置的结果.
 * 这里使用了递归.
 *
 * @param i 第i行放置皇后
 * @param n 总共的行数
 */
private static void traceBack(int i, int n) {
    if (i >= n) {
        recordAns(queues);
    } else {
        for (int j = 0; j < n; j++) {
            queues[i] = j;
            if (canPut(i)) {
                traceBack(i + 1, n);
            }
        }
    }
}

/**
 * @param qRecord 记录下来的棋子拜访位置,index是行号
 */
private static void recordAns(int[] qRecord) {
    List<String> singleAns = new ArrayList<>();
    for (int q : qRecord) {
        StringBuilder bu = new StringBuilder();
        for (int i = 0; i < qRecord.length; i++) {
            if (i == q) {
                bu.append("Q");
            } else {
                bu.append(".");
            }
        }
        singleAns.add(bu.toString());
    }
    ans.add(singleAns);
}

/**
 * 用来判断当前位置能否放置皇后.row是行,列的信息在全局变量的queues中.
 * 代码中i表示前面放置过皇后的行,queues[i]便是第i行,第queues[i]列放着皇后的意思
 * 所以这里循环是根据当前位置的上方其它位置判断当前位置能否放置皇后
 * Math.abs(row - i) == Math.abs(queues[row] - queues[i]):因为是±45°直线,所以|Δx|=|Δy|
 * queues[i] == queues[row]:同列.不能放置
 * 不需要判断同行的情况
 *
 * @param row 放置棋子的行号
 * @return 当前行是否可以放棋子
 */
private static boolean canPut(int row) {
    for (int i = 0; i < row; i++) {
        if (Math.abs(row - i) == Math.abs(queues[row] - queues[i]) || queues[i] == queues[row]) {
            return false;
        }
    }
    return true;
}

}

但是重点是另外一种解法

二进制解八皇后.

来自于JYGod丶的八皇后问题

代码:

public class NQueen {
​
private static final int N = 8; // 皇后数量，可拓展为N皇后
private static int count = 0; // 总方法数
private static int limit;
​
public static void main(String[] args) {
limit = (1 << N) - 1;
backtracking(0, 0, 0, 0);
System.out.println(count);
}
​
private static void backtracking(int a, int b, int c, int depth) {
if (depth == N) {
count++;
return;
}
int d = a | b | c;
while (d < limit) {
int bit = (d + 1) & ~d;
backtracking(a | bit, limit & ((b | bit) >> 1), limit & ((c | bit) << 1), depth + 1);
d |= bit;
}
}
}