第七章 n-steps Bootstrapping 读书笔记

目录

• 7.1 n步TD预测
  • • n-steps公式
    • 算法伪代码
• 7.2 n步Sarsa
  • • n-steps 公式
    • n-step sarsa backup
    • n-step sarsa for estimating Q
    • off-policy n-step sarsa
• 7.3 基于重要性采样的n步离策略学习
• 7.4 *带有控制变量的每步离策略方法
• 7.5 无重要性采样的离策略学习：n步反向传播树算法
  • • backup diagram
    • n-step tree backup 伪代码
• 7.6 *一个统一的算法： n-step Q(σ)
  • • backup diagram
    • 伪代码
• 7.7 总结

7.1 n步TD预测

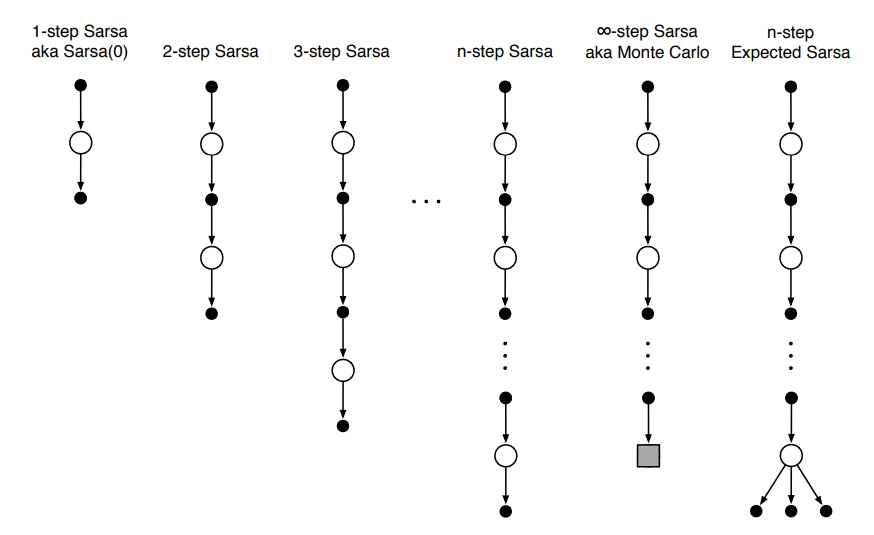
一步TD方法是等一个时间步数后根据下一个状态的估计值自举计算，而蒙特卡洛方法是等所有的时间步数完成后进行计算，n步自举是中间的任何数，可以是二步自举，也可以是三步自举···下图展示了三者之间的区别。

这种方法仍然是TD方法，是因为仍然是根据后来的估计值的差别来更行之前的估计值，只不过在n步之后才进行更新，所以叫n步TD方法。

n-steps公式

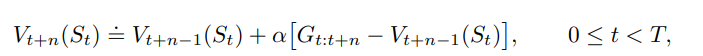
算法伪代码

7.2 n步Sarsa

n-steps 公式

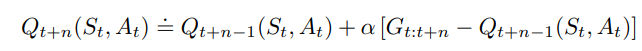
n-step sarsa backup

n-step sarsa for estimating Q

off-policy n-step sarsa

7.3 基于重要性采样的n步离策略学习

7.4 *带有控制变量的每步离策略方法

7.5 无重要性采样的离策略学习：n步反向传播树算法

backup diagram

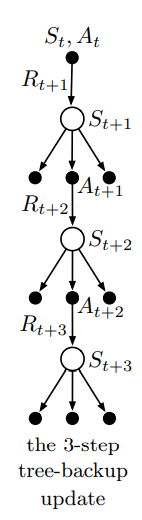
n-step tree backup 伪代码

7.6 *一个统一的算法： n-step Q(σ)

backup diagram

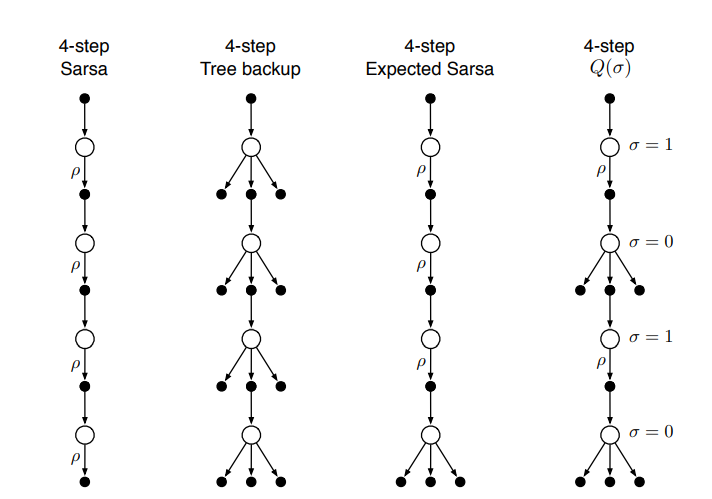
伪代码

7.7 总结

在这一章中我们在时序差分学习和蒙特卡洛方法中拓宽了TD方法。实验证明在中间步数的自举方法是十分重要的，要比两种极端情况下要表现得好。

我们在这一章的重点是n步方法，n步方法是向前多看了n个回报，状态和行为。N步自举的几个缺点：更新有n步的延迟，计算和内存要求比较高。在第12章用资格痕迹方法可以花费较少的计算和内存。

虽然n步自举比用资格痕迹花费大，但是它们的概念更加简单，我们也利用这个优势在n步的情况下把离线学习用两种方式来实现，一是通过重要性采样，而是基于反向传播树的更新。