一个有趣的四个正方形问题

从彭翕成老师的公众号上看到这样一道题：

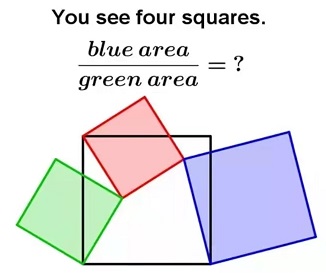
 想到了两种解法，在此记录一下。

解法一：如下图所示增加三条辅助线 DE、BC、DC：

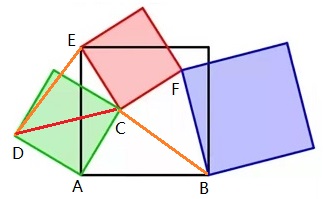
 △ADE 绕点 A 顺时针旋转 90 度与 △ACB 重合，于是 BC = DE 且 BC ⊥ DE.

这个结论用初二学生“规范”的推导方法会啰嗦不少，比如证明 BC = DE，需要指出 EA = AB，DA = AC，以及 ∠DAE = 90° - ∠EAC = ∠CAB，从而有 △ADE ≌ △ACB （SAS），于是 BC = DE；而证明 BC ⊥ DE，则需要延长 BC 分别交AE 和 DE 于点 G 和点 H，如下图所示：

 

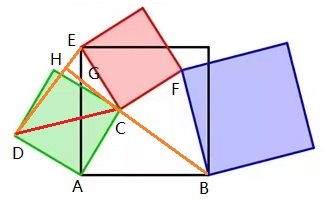
 考察 △EGH 和 △BGA，∠DEA = ∠CBA，∠EGH = ∠BGA，所以 ∠EHG = ∠GAB = 90°，于是 BC ⊥ DE.

接下来考察 △DEC 和 △BCF，此时已知 DE = BC，EC = CF，而 ∠DEC = ∠BCF（都和 ∠ECH 互余），即有

△DEC ≌ △BCF （SAS），于是 DC = BF，即 BF² = DC² = AC² + AD² = 2AC²，所以原题要求的面积比值为 2.

一点补充：△DEC 绕点 C 逆时针旋转 90 度再经平移就和 △BCF 重合了，DC 和 BF 除了相等，还有相互垂直的关系 。

解法二：使用解析几何的方法，不需要做辅助线。设上图中的点 A 为原点，并设黑色正方形边长为 1，在上图中构造直角平面坐标系，点 E 为 (0, 1)，点 B 为 (1, 0)，设点 C 为 (u, v)，点 F 为 (x, y)，则 直线 EC 的斜率为 (v - 1) / u，于是直线 FC 的斜率为 u / (1 - v)，即有：

(y - v) / (x - u) = u / (1 - v)    ①

由 EC = FC，有：

u² + (1 - v)² = (x - u)² + (y - v)²    ②

由 ① 有 y - v = u(x - u) / (1 - v)，代入 ②，得：

u² + (1 - v)² = (x - u)² · [1 + u² / (1 - v)²] =  (x - u)² · [u² + (1 - v)²] / (1 - v)²，即有

 (x - u)² = (1 - v)²，易知 x > u 和 1 > v，于是

x = u + 1 - v

代入 ①，得

y = u + v

FB² = (x - 1)² + y² = (u - v)² + (u + v)² = 2(u² + v²)

AC² = u² + v²

原题所求比值就是：FB² / AC² = 2.

 

补充：

彭老师的公众号上有位署名张老师的读者留言给出了相似三角形法的提示：连黑色正方形与红色正方形的对角线，得到一对相似三角形，立得蓝色正方形与绿色正方形边长之比。这个方法更加简洁巧妙，补充其完整过程作为解法三放到最后。

解法三：添加两条辅助线，即下图中的 DB 和 DF：

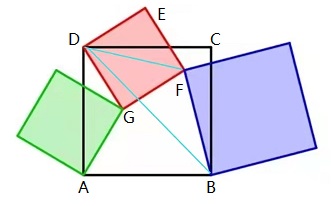
考察 △ADG 和 △BDF，显然有 AD : BD = DG : DF = 1 : 2^1/2，另外：

∠ADG = ∠ADB - ∠GDB

∠BDF = ∠FDG - ∠GDB

∠ADB = ∠FDG = 45°

即有 ∠ADG = ∠BDF，综上有 △ADG ∽ △BDF

于是原题所求比值就是：FB² / AG² = 2.

一点补充：△ADG 绕点 D 逆时针旋转 45 度，再放大 2^1/2 倍，就和 △BDF 重合了；另外图中 C、E 两点没有用到，可以不标注。