两道涂色题的解法与拓展分析

题1：如下图所示，10个方格排成一行。对每个方格进行涂色，三格涂成黑色，其余涂成白色，且要求相邻的任意三格中至多有一个黑格。求共有多少种涂色方案。

解法一：把黑格对应成数字1，白格对应成数字2，该问题可以等价成：

往7位数1221221的任意位置依次独立插入三个2，求形成的10位数中共有多少个不同取值。

以三个1为隔板，单独一个2可以插入的位置有4处：左边的1的左边、左边的1和中间的1之间、中间的1和右边的1之间以及右边的1的右边。第二处和第三处的位置可以再细分，但形成的新数数值不变，都应视作一处。

往上述4处位置插入两个2，分成两种情形：两个2不分开，有4种插法；两个2分开，有C(4,2)=6种插法。一共有4+6=10种插法。

往上述4处位置插入三个2，分成三种情形：三个2不分开，有4种插法；两个2不分开另一个分开，有C(4,1)·C(3,1)=12种插法；三个2分开，有C(4,3)=4种插法。一共有4+12+4=20种插法。即等价问题有20个不同取值。原题有20种涂色方案。

解法二：记三个黑格隔开的4个白格条中的白格数目分别为p、q、r和s。则有如下方程：

p+q+r+s=7      ①

其中p、q、r、s为整数，且满足p ≥ 0、q ≥ 2、r ≥ 2、s ≥ 0

设x=p+1，y=q-1，z=r-1，w=s+1，则有如下等价方程：

x+y+z+w=7      ②

其中x、y、z、w均为不小于1的整数。由插板法知，方程②的解数为C(6,3)=20。于是方程①的解数也为20。即原题有20种涂色方案。

题1的拓展题：n个方格排成一行。将其中m个方格涂成黑色，其余涂成白色，且要求任意相邻的t个方格中至多只有一个黑格。n、m、t满足2 ≤ t ≤ n/(m-1)，m > 1。求共有多少种涂色方案。

解：由m个黑格隔开的m+1个白格条中的白格数目分别记为X0、X1、...、Xm，则有如下m+1元一次不定方程：

X0+X1+...+Xm = n-m    ③

其中，Xi ≥ 0, i=0,m；Xj ≥ t-1, j=1,2,...,m-1

设

Yi=Xi+1,  i=0,m

Yj=Xj-(t-2),  j=1,2,...,m-1

则有如下等价的m+1元一次不定方程：

Y0+Y1+...+Ym = s      ④

其中每个变量均为不小于1的整数，且

s = n-m+2-(m-1)(t-2) = n-m+2-mt+2m+t-2 = n+m+t-mt

于是由插板法知，方程④的解数为C(n+m+t-mt-1,m)。这便是拓展题的涂色方案种数的通解表达式。

附言：

题1的解法二使用的插板法和换元法在由特定情形的求解转向一般情形的求解都很关键。

 

题2：如下图所示，10个方格排成一行。对每个方格进行涂色，一个方格只能涂成黑色或白色，且要求相邻的任意两格中至多有一个黑格。求共有多少种涂色方案。

解法一：沿用题1采用的换元法和插板法

10格中黑格数为0时，有C(10,0)=1种涂色方案

10格中黑格数为1时，有C(10,1)=10种涂色方案

10格中黑格数为2时，由题1的扩展题给出的通解式子，知对应的涂色方案种数为C(10+2+2-2·2-1,2)=C(9,2)=36

同样地，有

10格中黑格数为3时，涂色方案种数为C(10+3+2-3·2-1,3)=C(8,3)=56

10格中黑格数为4时，涂色方案种数为C(10+4+2-4·2-1,4)=C(7,4)=35

10格中黑格数为5时，涂色方案种数为C(10+5+2-5·2-1,5)=C(6,5)=6

于是所求的涂色方案种数共计为

ΣC(11-k,k)|k:0,5 = 1+10+36+56+35+6 = 144

解法二：按从左边数第5格的不同涂色分情形考虑：

（1）涂成白色，得到左右两个独立条，左边的有4格，右边的有5格；

（2）涂成黑色，得到左右两个独立条，左边的有3格，右边的有4格。

记n格独立条满足题设条件（即：对每个方格进行涂色，一个方格只能涂成黑色或白色，且要求相邻的任意两格中至多有一个黑格）的涂色方案种数为F(n)。由上面的划分，可得

F(10)=F(4)·F(5)+F(3)·F(4)

继续使用这种降阶法，可有

F(4)=F(1)·F(2)+F(0)·F(1)

F(5)=F(2)·F(2)+F(1)·F(1)

F(3)=F(1)·F(1)+F(0)·F(0)

其中F(0)=1，为了格式的一致性而引入。

单格独立条有两种涂色方案（白，黑），即F(1)=2；两格独立条有三种涂色方案（白白、白黑、黑白），即F(2)=3。

F(3)=2·2+1=5，F(4)=2·3+1·2=8，F(5)=3·3+2·2=13

于是所求的涂色方案种数为

F(10)=F(4)·F(5)+F(3)·F(4)=8·13+5·8=144

题2的拓展题：n个方格排成一行。对每个方格进行涂色，一个方格只能涂成黑色或白色，且要求相邻的任意两格中至多有一个黑格。求共有多少种涂色方案。

解：按左数第一格分情形考虑，会得到

F(n)=F(n-1)+F(n-2)

这里F(n)对应的数列为：2,3,5,8,13,21,34,...

斐波那契数列为：1,1,2,3,5,8,13,21,34,...

即F(n)对应的数列比斐波那契数列少了打头的两个1。

由斐波那契数列通项公式，可知

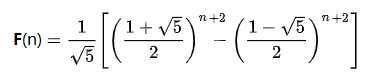
附言：

题2的解法二在发现F(n)对应斐波那契数列是很直观的。而且这个涂色模型还可以用来直观地研究斐波那契数列的一些特性。比如：

F(2n+1) = F²(n) + F²(n-1)

 

综合拓展题：如下图所示，10个方格排成一行。对每个方格进行涂色，一个方格只能涂成黑色或白色，且要求相邻的任意三格中至多有一个黑格。求共有多少种涂色方案。

解法一：记n格独立条满足题设条件（即：对每个方格进行涂色，一个方格只能涂成黑色或白色，且要求相邻的任意三格中至多有一个黑格）的涂色方案种数为G(n)。

按左数第一格分情形考虑：

（1）涂成黑色，则左2和左3两格都只能涂为白色，右边7格构成了7格独立条，即此情形下涂色方案种数为G(7)；

（2）涂成白色，此此情形下涂色方案种数为G(9)。

即G(10)=G(7)+G(9)

依次类推，可有

G(9)=G(6)+G(8)

G(8)=G(5)+G(7)

G(7)=G(4)+G(6)

G(6)=G(3)+G(5)

G(5)=G(2)+G(4)

G(4)=G(1)+G(3)

单格独立条有两种涂色方案（白，黑），即G(1)=2；

两格独立条有三种涂色方案（白白、白黑、黑白），即G(2)=3；

三格独立条有4种涂色方案（白白白、白白黑、白黑白、黑白白），即G(3)=4。

G(4)=2+4=6

G(5)=3+6=9

G(6)=4+9=13

G(7)=6+13=19

G(8)=9+19=28

G(9)=13+28=41

G(10)=19+41=60

即满足题设条件有60种涂色方案。

解法二：使用题1的拓展题推出的通解表达式C(n+m+t-mt-1,m)，这里n=10，t=3，由t ≤ n/(m-1)知m=2,3,4

10格中黑格数为0时，有C(10,0)=1种涂色方案

10格中黑格数为1时，有C(10,1)=10种涂色方案

10格中黑格数为2时，有C(10+2+3-2·3-1,2)=C(8,2)=28种涂色方案

10格中黑格数为3时，有C(10+3+3-3·3-1,3)=C(6,3)=20种涂色方案

10格中黑格数为4时，有C(10+4+3-4·3-1,4)=C(4,4)=1种涂色方案

于是，满足题设条件有1+10+28+20+1=60种涂色方案。