用一条同类辅助线证明勾股定理、海伦公式、正弦定理和余弦定理

一、勾股定理

求证：直角三角形的两条直角边的平方和等于斜边的平方。

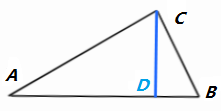
证明：如上图所示，△ABC为直角三角形，在斜边上作高CD。

 易知△ACD、△CBD、△ABC两两相似，于是有

AC:CD:AD=CB:BD:CD=AB:BC:AC

即有

AC²=AD·AB

BC²=BD·AB

于是AC²+BC²=(AD+BD)·AB=AB²。

 

二、海伦公式

 求证：对任意三角形，有

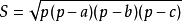　　　　①

公式中a，b，c分别为三角形三边长，p为半周长，S为三角形的面积。

证明：在三角形的三条边的最长边（不妨设为AB边）上作高，仍沿用前图（不再要求AC⊥BC）。记AB=c，BC=a，AC=b，AD=x。由勾股定理有

CD² = b² - x² = a² - (c - x)² = a² - c² - x² + 2cx

即有

2cx = b² + c² - a²

于是

16S² = 4c²·CD² = 4c²(b² - x²) = 4c²b² - (2cx)²

 = 4b²c² - (b² + c² - a²)²　　　　②

 = (2bc + b² + c² - a²)(2bc - b² - c² + a²)

 = [(b+c)² - a²]·[a² - (b-c)²]　　　　③

 = (a+b+c)(b+c-a)(a+c-b)(a+b-c)　　④

 = 2p·(2p-2a)·(2p-2b)·(2p-2c)

= 16p(p-a)(p-b)(p-c)

即有

S² = p(p-a)(p-b)(p-c)

两边开平方，即为海伦公式。

附言：

海伦公式上述推导过程中出现的等式②、③和④，在实际计算三角形面积时往往比等式①更为方便。比如a、b、c分别为根号3、根号5、根号7时，使用等式④或①时都需要倒推到等式③或②，然后再计算。

等式②和③不太好记忆，但等式④对称性很好，和等式①一样好记。有了④或①，可以很容易推出③和②。

由等式④可以倒推出等式③和②的另两个表示式，即有如下完整的表示式：

16S² =  [(b+c)² - a²]·[a² - (b-c)²] = [(a+b)² - c²]·[c² - (a-b)²] =  [(a+c)² - b²]·[b² - (a-c)²]

16S² = 4b²c² - (b² + c² - a²)² = 4a²b² - (a² + b² - c²)² = 4a²c² - (a² + c² - b²)²

 

三、正弦定理

求证：对任意三角形，角A、B、C所对的边长分别为a、b、c，则有

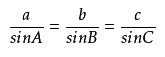
证明：仍沿用前图，同样在在最长边（不妨假设为AB）上作高，由正弦定义，有

CD = b·sinA = a·sinB，即有

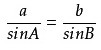
而对于最大角∠C，则需要分情形考虑：

1、∠C为锐角，则作BC边上的高AE，如下图所示：

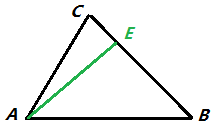
由正弦定义，有

AE = b·sinC = c·sinB

2、∠C为直角，上图中点E和点C重合，有AC = b = c·sinB，由sin90°=1，同样有

b·sinC = c·sinB

3、∠C为钝角，依然作BC边上的高AE，如下图所示：

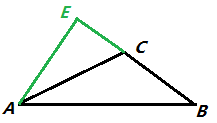
由正弦定义，有

AE = b·sinC = c·sinB

综上，所证命题成立。

 

四、余弦定理

求证：对任意三角形，角A、B、C所对的边长分别为a、b、c，则有

a² = b² + c² - 2bc·cosA

b² = a² + c² - 2ac·cosB

c² = a² + b² - 2ab·cosC

证明：在三角形的三条边的最长边（不妨设为AB边）上作高，如下图所示。

记AD=x。和前面推导海伦公式一样，由勾股定理有

CD² = b² - x² = a² - (c - x)² = a² - c² - x² + 2cx

即有

2cx = b² + c² - a²

再由AD = AC·cosA，即x = b·cosA，有

2bc·cosA = b² + c² - a²，即

a² = b² + c² - 2bc·cosA

同样，记BD=y。由勾股定理有

CD² = a² - y² = b² - (c - y)² =  b² - c² - y² + 2cy

即有

2cy = a² + c² - b²

再由BD = BC·cosB，即y = a·cosB，有

2ac·cosB = a² + c² - b²，即

b² = a² + c² - 2ac·cosB

对于最大角∠C，则需要分情形考虑：

1、∠C为锐角，则作BC边上的高AE，如下图所示：

记CE=x。由勾股定理有

AE² = b² - x² = c² - (a - x)² = c² - a² - x² + 2ax，于是有

2ax = b² + a² - c²

代入x = b·cosC，即有

c² = a² + b² - 2ab·cosC

2、∠C为直角，上图中点E和点C重合，有cosC=cos90°=0，自然有

c² = a² + b² - 2ab·cosC

3、∠C为钝角，依然作BC边上的高AE，如下图所示：

记CE=x。由勾股定理有

AE² = b² - x² = c² - (a + x)² = c² - a² - x² - 2ax，于是有

-2ax = b² + a² - c²

由于∠ACB为钝角，有x = -b·cosC，于是有

2ab·cosC = b² + a² - c²

c² = a² + b² - 2ab·cosC

综上，所证命题成立。