一个梯形面积题的分析与求解

 如下图，ABCD为梯形，另有BC=2AD，AE=2BE，CF=2DF。点G在EF上，三角形BEG和CFG面积都为20，求该梯形的面积。

 

 

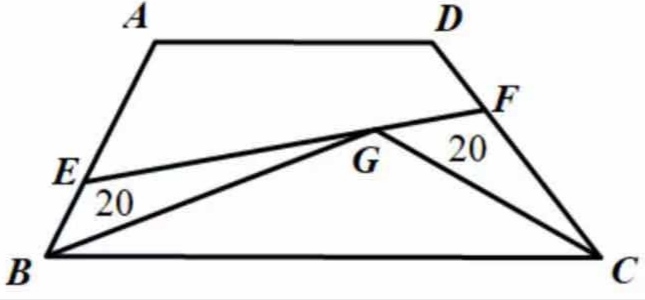
分析：这题的关键是想到如何利用梯形下底长是上底长的两倍这个信息。延长梯形的两条腰交出一个顶点，这题就会迎刃而解。

解：如下图所示添加辅助线（延长BA和CD，交于点H；连接HG）

 

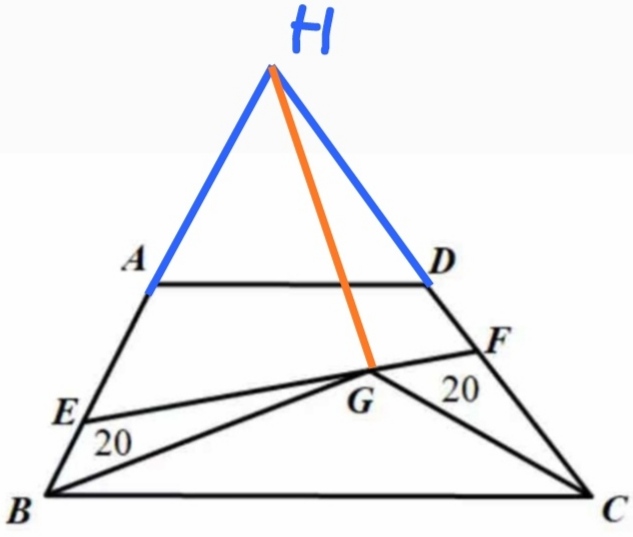
易知HA=AB和HD=DC；又由AE=2BE，易知HE=5BE，于是三角形HEG的面积为三角形BEG的5倍，即为20*5=100。

同样的方法，可得三角形HFG的面积为40。于是三角形HEF的面积为100+40=140。

设三角形HAD的面积为x，由鸟头模型有

x/140=HA*HD/(HE*HF)=(HA/HE)*(HD/HF)=(3/5)*(3/4)=9/20，求解得x=63。

于是梯形面积为63*3=189。