横平竖直作辅助线法求解面积的两道题

题1：如下图，以EF为直径的半圆与长方形ABCD的每条边恰有一个交点。EF=20，FC=2。求阴影部分的面积。

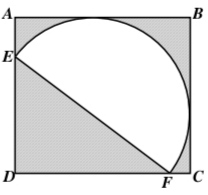
分析：只要求出长方形的长和宽就好。

解：按下图添加辅助线：

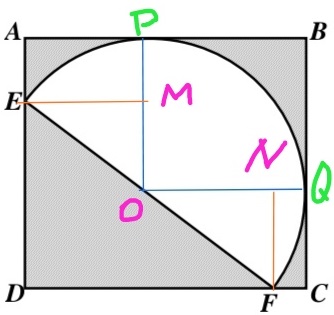
易知EM=ON=OQ-NQ=20/2-2=8，于是得到长方形的长为EM+OQ=8+10=18。

FN*FN=OF*OF-ON*ON=100-64=36，故FN=6，于是得到长方形的宽为6+10=16。

所求阴影部分的面积为16*18-50Π。

 

题2：下图的正方形被分成了面积相等的五块。已知AB长为3.6厘米，求该正方形的面积。

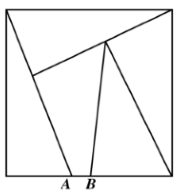
分析：这题乍一看面积五等分的选点似乎是比较随意的，仔细观察其实不然。结合下图（三条辅助线GH、MJ、MN分别垂直于CD、DE、FE）说明一下：

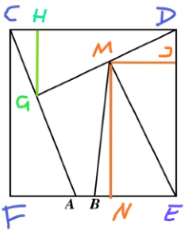
由左下角的直角三角形CFA可知点A在正方形底边FE上的位置是固定的，FA的长度为正方形边长的2/5；再考察上侧的三角形CDG，可知点G在线段CA上的位置也是固定的，图中GH的长度同样为边长的2/5；同样，继续考察右侧的三角形DEM，可知点M在线段DG上的位置是固定的，图中MJ的长度为边长的2/5；继续考察三角形EMB，可知点B在FE上的位置也是固定的。

由上面的分析可知，只要能把线段MN的长度用边长表示出来，线段BE的长度就也可用边长表示出来，再结合AB的长度就能够求出边长。

解：在上图中再作一条辅助线，过点G做CD的平行线，分别交CF、DE于点P、Q，如下图所示：

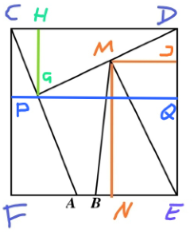
设正方形的边长为5t，则由题设条件可知FA=2t，MJ=2t，CP=HG=2t。

CPG和CFA是一对相似三角形，有CP/CF=PG/FA，即2t/5t=PG/2t，于是求得PG=4t/5，GQ=5t-4t/5=21t/5。

DMJ和DGQ是一对相似三角形，有DJ/DQ=MJ/GQ，于是DJ=2t*2t/(21t/5)=20t/21，MN=DE-DJ=5t-20t/21=85t/21。

由BE*MN=5t*2t，有BE=210t/85=42t/17。

由AE=AB+BE，有3t=3.6+42t/17，解得t=6.8，于是所求正方形面积为5t*5t=34*34=1156平方厘米。