【HDOJ 2837】Calculation 欧拉降幂
根据欧拉定理,可降幂:
有亿些坑点,其中一个值得注意的是不管指数b和\(\phi[m]\)的大小关系,都可以先对\(\phi[m]\)取模,看最后还需不需要加上\(\phi[m]\)即可
细节见代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m;
int t;
ll phi(ll n){
ll nn=n;
ll ans=n;
for(ll i=2;i*i<=nn;i++){
if(n%i==0){
ans=ans-ans/i;
while(n%i==0){
n/=i;
}
}
}
if(n>1){
ans=ans-ans/n;
}
return ans;
}
ll Pow(ll a,ll b,ll mod){
ll ans=1;
while(b){
if(b%2){
ans*=a;
ans%=mod;
}
a*=a;
a%=mod; //注意这里也需要取模
b/=2;
}
if(ans==0) ans+=mod; ////
return ans;
}
ll sum(ll a,ll b,ll m){
ll ans=1;
for(int i=1;i<=b;i++){
ans*=a;
if(ans>=m) return ans;
}
return ans;
}
ll f(ll n,ll m){ //f(n) % m
if(m==1) return 0;
if(n==0) return 1;
if(n<10) return n;
ll phi_m=phi(m);
ll up=f(n/10,phi_m);
ll base=sum(n%10,up,phi_m);
if(base>=phi_m)
return Pow(n%10,up+phi_m,m);
else return base;
}
int main(){
cin>>t;
while(t--){
scanf("%d%d",&n,&m);
printf("%lld\n",f(n,m));
}
system("pause");
return 0;
}



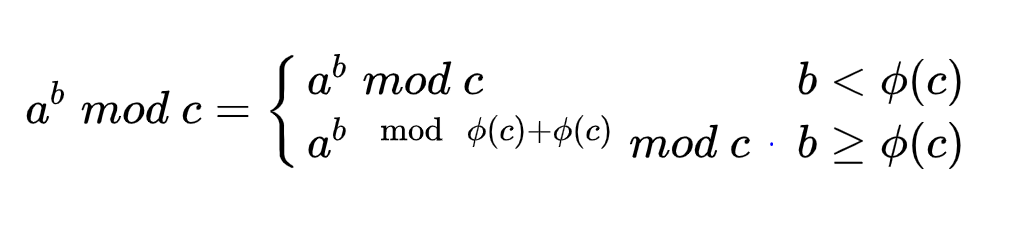

 浙公网安备 33010602011771号
浙公网安备 33010602011771号