哈希表模拟散列表

哈希表模拟散列表

题目链接：AcWing840

-10^9 ~ 10^9的数映射到0 ~ 10^5的区间上

把x映射到[0,N]区间上：

k = (x % N + N) % N;

---

问题: 为什么要 +N ?

在C++中是有负余数存在的,比如-10%3 = -1而实际上在数学里是这样子的，-10 % 3 = 2

在数学中有以下定义：
如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足a=qd+r且0 ≤ r < d（其中q为商，r为余数)。
此定义一般作为数学中的取余法则，即两个数取余，余数总是为正数。

---

拉链法

映射到某个位置如果存在冲突就插入链表。

因为要把某个很大的数映射到这个区间上需要取mod，我们要找的一个数N使得x mod N 之后冲突的概率最小、

因为要映射到[0,100000]，就找大于100000的最小的质数，这个质数就是要找的那个N

for(int i = 100000; ; i++)
{
	bool flag = true;
	
	for(int j = 2 ; j * j <= i ; j ++)
		if(i % j == 0) 
		{
			flag = false;
			break;
		}
	if(flag)
	{
		cout << i << endl;
		break;
	}
}

此题求质数可以求得N = 100003

拉链法insert

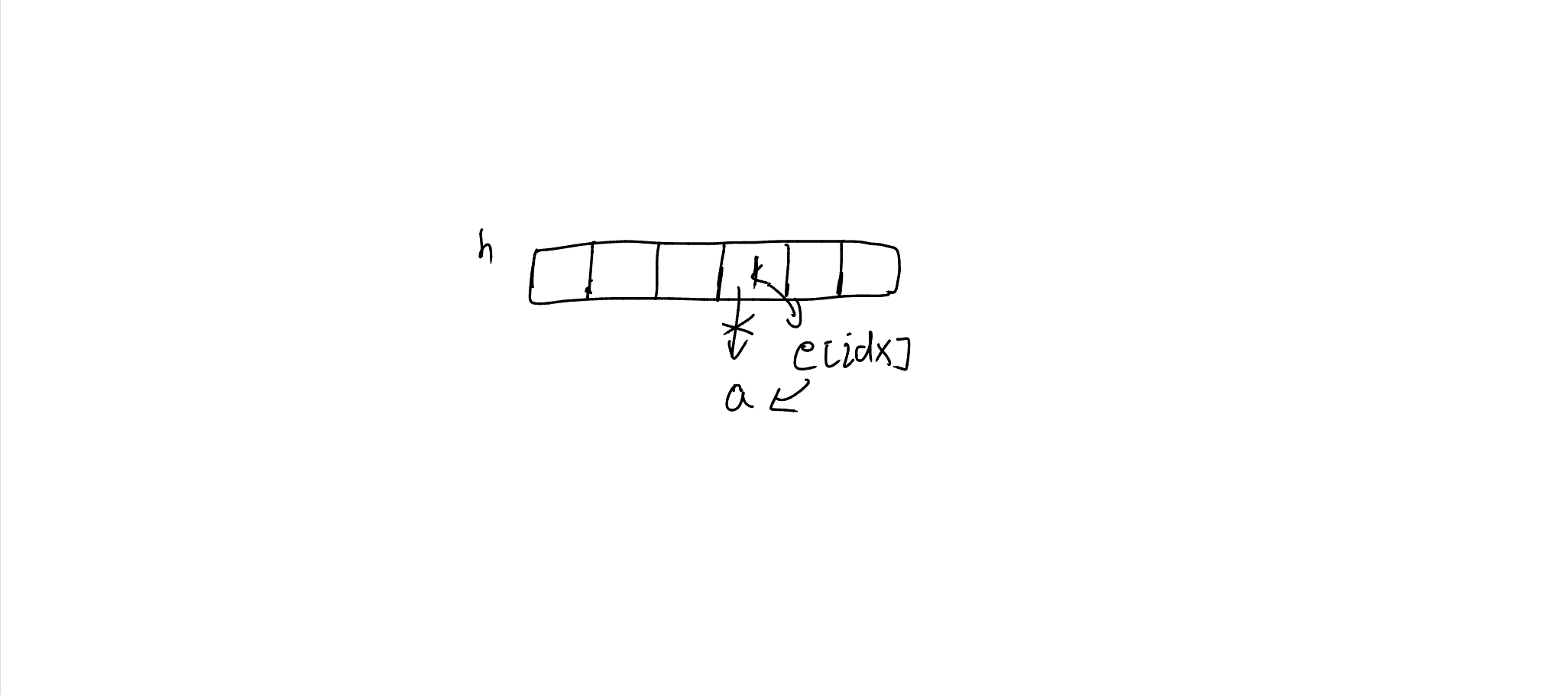
void insert(int x)
{
    int k = (x % N + N) % N;
    
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

拉链法find

bool find(int x)
{
	int k = (x % N + N) % N;
	for(int i = h[k] ; i != -1; i = ne[i])
	{
		int j = e[i];
		if(j == x) return true;
	}
	return false;
}

代码

#include<cstring>
#include<iostream>

using namespace std ;

const int N = 100003;

int h[N],e[N],ne[N],idx;

void insert(int x)
{
    int k = (x % N + N) % N;
    
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

bool find(int x)
{
	int k = (x % N + N) % N;
	for(int i = h[k] ; i != -1; i = ne[i])
	{
		int j = e[i];
		if(j == x) return true;
	}
	return false;
}

int main()
{
    int n;
    scanf("%d",&n);
    
    memset(h,-1,sizeof h);
    
    while(n --)
    {
        char op[2];
        int x;
        scanf("%s%d",op,&x);
        if(*op == 'I') insert(x);
        else
        {
            if(find(x)) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

开放寻址法(好用)

通常将数组开为原来的2~3倍

在插入一个数的时候，先去进行映射k = (x % N + N) % N. 如果k位置有数，就存在k+1,如果k+1有数就存在k+2,以此类推

只需写一个find(int x)即可.如果存在就返回x映射的下标,如果不存在就返回x应该在的映射位置

判断是否存在：如果k位置不是，k+1上为空就不存在.如果K不是，且k+1存在就往后判断.

int find(int x)
{
	int k = (x % N + N) % N;
	while(h[k] != null && h[k] != x)
	{
		k ++;
		if(k == N) k = 0;
	}
	
	return k;
}

代码

#include<cstring>
#include<iostream>

using namespace std ;

const int N = 200003, null = 0x3f3f3f3f; // 这里开到了原来的两倍

int h[N];

int find(int x)
{
	int k = (x % N + N) % N;
	while(h[k] != null && h[k] != x)
	{
	    k ++;
	    if(k == N) k = 0;
	}
	return k;
}

int main()
{
    int n;
    scanf("%d",&n);
    
    memset(h,0x3f,sizeof h);
    
    while(n --)
    {
        char op[2];
        int x;
        scanf("%s%d",op,&x);
        
        int k = find(x);
        if(*op == 'I') h[k] = x;
        else
        {
            if(h[find(x)] != null) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}