双重计数

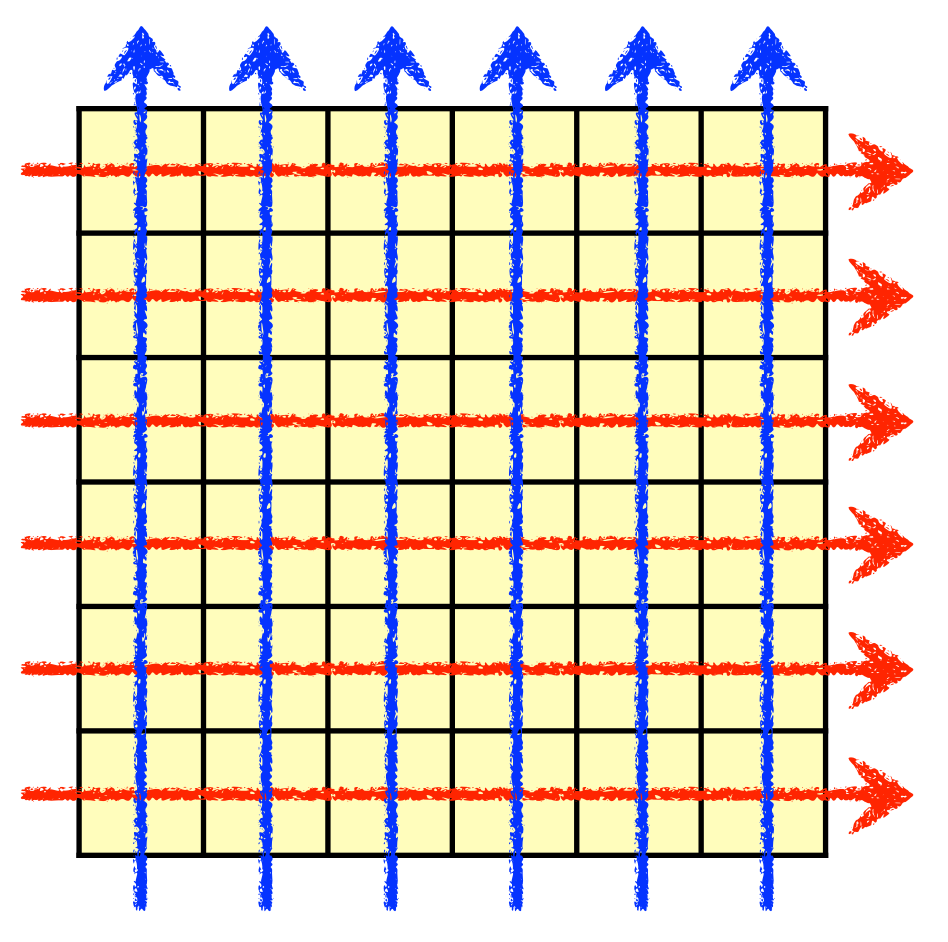
定理

\(\forall n,r,s\in\N\)，有

\[\binom{n}{r}\binom{r}{s}=\binom{n}{s}\binom{n-s}{r-s} \]

证明

考虑计算 \(|\{\langle A,B\rangle:|A|=r\land|B|=s\land B\subseteq A\subseteq\{1,2,\dots,n\}\}|\)。

1. 先枚举 \(A\) 再枚举 \(B\)。
2. 先枚举 \(B\) 再枚举 \(A\)。

推论

\(\forall n,m\in\N\)，有

\[\sum_{k=m}^n\binom{n}{k}\binom{k}{m}=\binom{n}{m}2^{n-m} \]

证明

\[\begin{align} \sum_{k=m}^n\binom{n}{k}\binom{k}{m}&=\binom{n}{m}\sum_{k=m}^n\binom{n-m}{k-m}\\ &=\binom{n}{m}\sum_{k=0}^{n-m}\binom{n-m}{k}\\ &=\binom{n}{m}2^{n-m} \end{align} \]

定理

记 \(F_n\) 为 Fibonacci 数列 的第 \(n\) 项。

\(\forall n\in\N\)，有

\[\sum_{i=0}^{n-1}F_i=F_{n+1}-1 \]

证明

引理

\(F_{n+1}\) 是用 \(1\times2\) 和 \(2\times1\) 的矩形铺满 \(2\times n\) 的网格的方案数。

证明

易证 \(n=0,1\) 时成立。

对于 \(n\ge2\)，考虑开头的矩形。若是 \(1\times2\) 的，依归纳假设得到方案数为 \(F_{n-1}\)。若是 \(2\times1\) 的，依归纳假设得到方案数为 \(F_n\)。应用加法原理得到方案数为 \(F_{n-1}+F_n=F_{n+1}\)。

考虑计算用 \(1\times2\) 和 \(2\times 1\) 的矩形铺满 \(2\times n\) 的网格，存在 \(1\times 2\) 的方案数。

1. 枚举第一个 \(1\times 2\) 的位置。
2. 在所有铺满的方案中减去不存在 \(1\times 2\) 的方案。

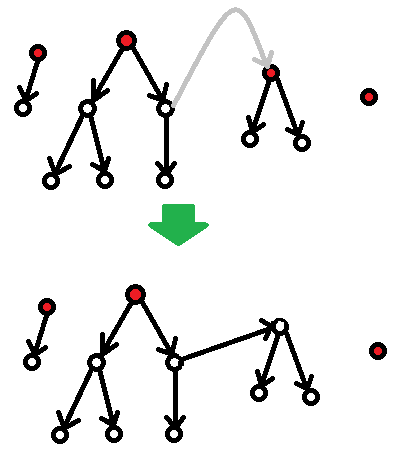
定理（Cayley 公式）

\(K_n\) 有 \(n^{n-2}\) 棵生成树。

证明

记 \(K_n\) 有 \(T_n\) 棵生成树。

考虑计算序列 \(\langle\langle u_1,v_1\rangle,\langle u_2,v_2\rangle,\dots,\langle u_{n-1},v_{n-1}\rangle\rangle\) 的个数，满足这 \(n-1\) 条有向边构成一棵顶点集为 \(\{1,2,\dots,n\}\) 的有根树。

1. 考虑给每棵无根树指定一个根，得到有 \(nT_n\) 棵有根树。对每个边集定序都恰有 \((n-1)!\) 种方案。应用乘法原理得到序列个数为 \(n!T_n\)。

2. 考虑依序加入每条有向边。加入第 \(i\) 条边前，图是由 \(n-i+1\) 棵树组成的森林。易证此时有向边 \(\langle u,v\rangle\) 可以加入图中当且仅当 \(v\) 是除 \(u\) 所在树之外的一棵树的根。故第 \(i\) 条边有 \(n(n-i)\) 种方案。应用乘法原理得到序列个数为 \(\prod_{i=1}^{n-1}n(n-i)=n^{n-1}(n-1)!\)。

综上有 \(n!T_n=n^{n-1}(n-1)!\)，即 \(T_n=n^{n-2}\)。

定理（Vandermonde 恒等式）

\[\binom{\sum_{i=1}^kn_i}{m}=\sum_{\sum_{i=1}^km_i=m}\prod_{i=1}^k\binom{n_i}{m_i} \]

证明

设 \(A_i=\{\langle i,1\rangle,\langle i,2\rangle,\dots,\langle i,n_i\rangle\}\)。考虑计算在 \(A_1,A_2,\dots,A_n\) 中选对，总共选 \(m\) 对的方案数。

1. 在 \(\bigcup_{i=1}^nA_i\) 中选 \(m\) 对。
2. 枚举每个集合中选的对数。

推论

\[\sum_{k=0}^{n}\binom{n}{k}^2=\binom{2n}{n} \]

定理

任取简单无向图 \(G=\langle V,E\rangle\)，若 \(G\) 不含三元环，那么

\[|E|\le\frac{|V|^2}{4} \]

证明

设 \(d_v\) 为顶点 \(v\) 的度数。

引理

\[\forall\{u,v\}\in E,d_u+d_v\le|V| \]

证明

若 \(d_u+d_v>|V|\)，那么 \((d_u-1)+(d_v-1)>|V|-2\)。应用鸽巢原理有 \(\exist w\in V,\{u,w\}\in E\land\{v,w\}\in E\)。那么 \(\{\{u,v\},\{v,w\},\{w,u\}\}\) 是 \(G\) 中的三元环。故 \(d_u+d_v\le|V|\)。

\[\begin{align} |V||E|&\ge\sum_{\{u,v\}\in E}(d_u+d_v)\\ &=\sum_{v\in V}d_v^2\\ \end{align} \]

应用 Cauchy-Schwarz 不等式得

\[\begin{align} \sum_{v\in V}d_v^2&\ge\frac{(\sum_{v\in V}d_v)^2}{|V|}\\ &=\frac{4|E|^2}{|V|} \end{align} \]

综上

\[|E|\le\frac{|V|^2}{4} \]

定理

任取简单平面连通图 \(G=\langle V,E\rangle\)。设 \(d_v\) 为顶点 \(v\) 的度数。\(\exist v\in V,d_v<6\)。

证明

易证 \(|V|<3\) 时成立。设 \(|V|\ge3\)。

若 \(\forall v\in V,d_v\ge6\)，有

\[\begin{align} 2|E|&=\sum_{v\in V}d_v\\ &\ge6|V| \end{align} \]

即

\[|E|\ge3|V| \]

\(|V|\ge3\) 时有 \(|E|\le3|V|-6\)。故 \(\exist v\in V,d_v<6\)。

推论（六色定理）

任取简单平面图 \(G=\langle V,E\rangle\)。存在一种 \(6\)-染色方案，满足 \(\forall\{u,v\}\in E\)，\(u,v\) 颜色不同。

证明

只需证 \(G\) 连通的情况。

易证 \(V=\empty\) 时成立。

对于 \(|V|>0\) 的图，设 \(v\) 是一个满足 \(d_v<6\) 的顶点。依归纳假设存在 \(G-v\) 的染色方案。应用鸽巢原理得到存在 \(v\) 的邻居中未出现的颜色。

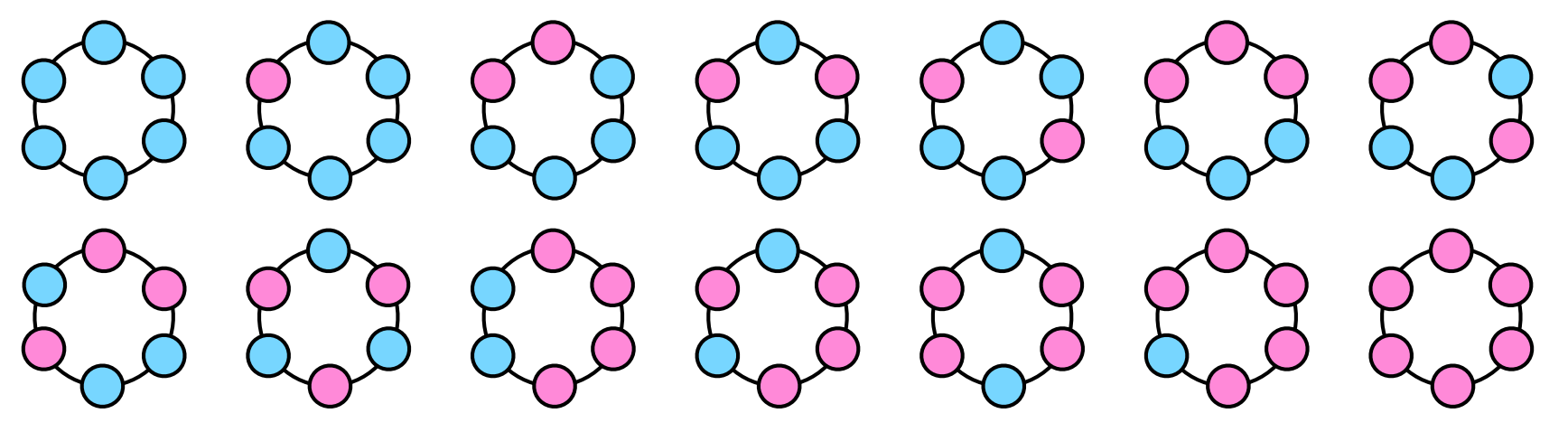
定理

设顶点集 \(V=\{0,1,\dots,n-1\}\)，边集 \(E=\{\{v,(v+1)\bmod n\}:v\in V\}\)，图 \(G=\langle V,E\rangle\)。

定义 \(G\) 的两种 \(k\)-染色方案 \(\langle c_0,c_1,\dots,c_{n-1}\rangle\) 和 \(\langle c'_0,c'_1,\dots,c'_{n-1}\rangle\)「本质相同」当且仅当

\[\exist i\in\{0,1,\dots,n-1\},\forall v\in V,c_{v}= c'_{(i+v)\bmod n} \]

易证「本质相同」是等价关系。

那么 \(G\) 的「本质不同」的 \(k\)-染色方案数为

\[\frac{1}{n}\sum_{d|n}k^{\frac{n}{d}}\varphi(d) \]

证明

记 \(G\) 的「本质不同」的 \(k\)-染色方案数为 \(T_{n,k}\)。取 \(T_{n,k}\) 个「本质不同」的 \(k\)-染色方案记做 \(c_1,c_2,\dots,c_{T_{n,k}}\)。

考虑一张 \(T_{n,k}\times n\) 的表格，其中第 \(i\) 行第 \(j\) 列是 \(c_i\) 的 \(j\) 次循环移位。

考虑计算表格内序列个数。

1. 根据定义得到序列个数为 \(nT_{n,k}\)。
2. 考虑每种 \(k\)-染色方案的出现次数。易证相同方案只会出现在同一行。

于是有

\[\begin{align} nT_{n,k}&=\sum_{a}\sum_{i=1}^n[\langle a_0,a_1,\dots,a_{n-1}\rangle=\langle a_{i\bmod n},a_{(i+1)\bmod n},\dots,a_{i-1}\rangle]\\ &=\sum_{i=1}^n\sum_{a}[\langle a_0,a_1,\dots,a_{n-1}\rangle=\langle a_{i\bmod n},a_{(i+1)\bmod n},\dots,a_{i-1}\rangle]\\ &=\sum_{i=1}^nk^{\gcd(i,n)}\\ &=\sum_{d|n}k^d\sum_{i=1}^n[\gcd(i,n)=d]\\ &=\sum_{d|n}k^d\sum_{i=1}^{\frac{n}{d}}[\gcd(i,\frac{n}{d})=1]\\ &=\sum_{d|n}k^d\varphi(\frac{n}{d})\\ &=\sum_{d|n}k^\frac{n}{d}\varphi(d) \end{align} \]

即

\[T_{n,k}=\frac{1}{n}\sum_{d|n}k^\frac{n}{d}\varphi(d) \]

推论

\(G\) 的「本质不同」的 \(k\)-染色方案中，要求每种颜色都出现的方案数为

\[\frac{k!}{n}\sum_{d|n}\varphi(d){\frac{n}{d}\brace k} \]

证明

记 \(G\) 的「本质不同」的 \(k\)-染色方案中，要求每种颜色都出现的方案数为 \(S_{n,k}\)。

易证

\[T_{n,k}=\sum_{i=0}^k\binom{k}{i}S_{n,i} \]

应用二项式反演得

\[\begin{align} S_{n,k}&=\sum_{i=0}^k(-1)^{k-i}\binom{k}{i}T_{n,i}\\ &=\sum_{i=0}^k(-1)^{k-i}\binom{k}{i}\frac{1}{n}\sum_{d|n}i^\frac{n}{d}\varphi(d)\\ &=\frac{1}{n}\sum_{d|n}\varphi(d)\sum_{i=0}^k(-1)^{k-i}\binom{k}{i}i^\frac{n}{d}\\ &=\frac{k!}{n}\sum_{d|n}\varphi(d)\sum_{i=0}^k\frac{(-1)^{k-i}i^\frac{n}{d}}{i!(k-i)!}\\ &=\frac{k!}{n}\sum_{d|n}\varphi(d){\frac{n}{d}\brace k} \end{align} \]

推论

\(G\) 的「本质不同」的 \(k\)-染色方案中，不含小于 \(n\) 的循环节的方案数为

\[\frac{1}{n}\sum_{d|n}k^\frac{n}{d}\mu(d) \]

证明

记 \(G\) 的「本质不同」的 \(k\)-染色方案中，不含小于 \(n\) 的循环节的方案数为 \(M_{n,k}\)。

易证

\[T_{n,k}=\sum_{d|n}M_{d,k} \]

令 \(T(n)=T_{n,k},M(n)=M_{n,k},K(n)=k^n\)。

那么就有

\[\begin{align} M*1&=T\\ \operatorname{id}\cdot(M*1)&=K*\varphi\\ \operatorname{id}\cdot M*\operatorname{id}&=K*\mu*\operatorname{id}\\ \operatorname{id}\cdot M&=K*\mu \end{align} \]

即

\[M_{n,k}=\frac{1}{n}\sum_{d|n}k^\frac{n}{d}\mu(d) \]

定理

\(\forall x\in\mathbb{C},n\in\N\)，有

\[x^{\overline{n}}=\sum_{k=0}^n{n\brack k}x^k \]

证明

设 \(x\in\N\)。

考虑计算选择一个排列 \(p\in S_n\)，并将 \(p\) 的每个轮换染色的方案数。共有 \(x\) 种颜色。

1. 考虑依次插入 \(1,2,\dots,n\)。若 \(i\) 的后继是自己，那么有 \(x\) 种选颜色的方案。若 \(i\) 的后继不是自己，那么有 \(i-1\) 个可以选择的后继。应用加法原理得到插入 \(i\) 共有 \(x+i-1\) 种方案。应用乘法原理得到共有 \(\prod_{i=1}^n(x+i-1)=x^{\overline{n}}\)。
2. 考虑枚举轮换个数后分别对每个轮换上色。

综上，\(x\in\N\) 时有

\[x^{\overline{n}}=\sum_{k=0}^n{n\brack k}x^k \]

易证两边都是关于 \(x\) 的 \(n\) 次多项式，且在无穷多个点上相等，故 \(x\in\mathbb{C}\) 时均成立。

推论

\(\forall x\in\mathbb{C},n\in\N\)，有

\[x^{\underline{n}}=\sum_{k=0}^n(-1)^{n-k}{n\brack k}x^k \]

证明

\[\begin{align} x^{\underline{n}}&=(-1)^n(-x)^{\overline{n}}\\ &=(-1)^n\sum_{k=0}^n{n\brack k}(-x)^k\\ &=\sum_{k=0}^n(-1)^{n-k}{n\brack k}x^k \end{align} \]

推论

\(\forall n\in\Z^+\)，长度为 \(n\) 且有偶数个轮换的排列有 \(\lfloor\frac{n!}{2}\rfloor\) 个。

证明

\[\begin{align} \sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}{n\brack 2k}&=\frac{\sum_{k=0}^n{n\brack k}1^k+\sum_{k=0}^n{n\brack k}(-1)^k\\}{2}\\ &=\frac{1^{\overline{n}}+(-1)^{\overline n}}{2}\\ &=\lfloor\frac{n!}{2}\rfloor \end{align} \]

推论

\(\forall n\in\Z^+\)，长度为 \(n\) 且有奇数个轮换的排列有 \(\lceil\frac{n!}{2}\rceil\) 个。

证明

\[n!-\lfloor\frac{n!}{2}\rfloor=\lceil\frac{n!}{2}\rceil \]

定理

\(\forall x\in\mathbb{C},n\in\N\)，有

\[x^n=\sum_{k=0}^n{n\brace k}x^{\underline{k}} \]

证明

设 \(x\in\N\)。

考虑计算将 \(n\) 个有区分的球放进 \(x\) 个有区分的盒子的方案数。

1. 应用乘法原理得到方案数为 \(x^n\)
2. 枚举非空盒子数量。\(n\) 个有区分的球放进 \(k\) 个无区分的盒子的方案数是 \(n\brace k\)。分配标号有 \(\binom{n}{k}k!=x^{\underline{k}}\) 种方案。应用乘法原理得到有 \(k\) 个非空盒子时方案数为 \({n\brace k}x^{\underline{k}}\)。

综上，\(x\in\N\) 时有

\[x^n=\sum_{k=0}^n{n\brace k}x^{\underline{k}} \]

易证两边都是关于 \(x\) 的 \(n\) 次多项式，且在无穷多个点上相等，故 \(x\in\mathbb{C}\) 时均成立。

推论

\(\forall x\in\mathbb{C},n\in\N\)，有

\[x^n=\sum_{k=0}^n{n\brace k}(-1)^{n-k}x^{\overline{k}} \]

证明

\[\begin{align} (-x)^n&=\sum_{k=0}^n{n\brace k}(-x)^{\underline{k}}\\ &=\sum_{k=0}^n{n\brace k}(-1)^kx^{\overline{k}}\\ x^n&=\sum_{k=0}^n{n\brace k}(-1)^{n-k}x^{\overline{k}} \end{align} \]

定理

任取 \(n\in\N\)，有

\[\frac{1}{n!}\sum_{k=0}^n{n\brack k}k=H_n \]

证明

均匀随机地取排列 \(p\in S_n\)。考虑计算 \(p\) 的轮换个数的期望。

1. 枚举轮换个数，有 \(n\brack k\) 个恰有 \(k\) 个轮换的排列。

2. 令 \(X\) 为 \(p\) 的轮换个数。若 \(a\) 是 \(p\) 的轮换，\(I(a)=1\)，否则 \(I(a)=0\)。

   易证

   \[X=\sum_a\frac{I(a)}{|a|} \]

   那么

   \[\begin{align} \mathbb{E}[X]&=\mathbb{E}\left[\sum_a\frac{I(a)}{|a|}\right]\\ &=\sum_a\frac{\mathbb{E}[I(a)]}{|a|}\\ &=\sum_a\frac{\Pr[I(a)=1]}{|a|}\\ &=\sum_{k=1}^n\frac{1}{k}\sum_{|a|=k}\Pr[I(a)=1]\\ &=\sum_{k=1}^n\frac{1}{k}\sum_{|a|=k}\frac{(n-k)!}{n!}\\ &=\sum_{k=1}^n\frac{1}{k}\binom{n}{k}k!\frac{(n-k)!}{n!}\\ &=\sum_{k=1}^n\frac{1}{k}\\ &=H_n \end{align} \]