卷积神经网络

卷积神经网络的一个重要思想是参数共享

卷积神经网络(CNN)是一种专门用来处理具有类似网络结构的数据的神经网络，例如时间序列数据和图像数据

卷积运算

卷积是对两个实变函数的一种运算
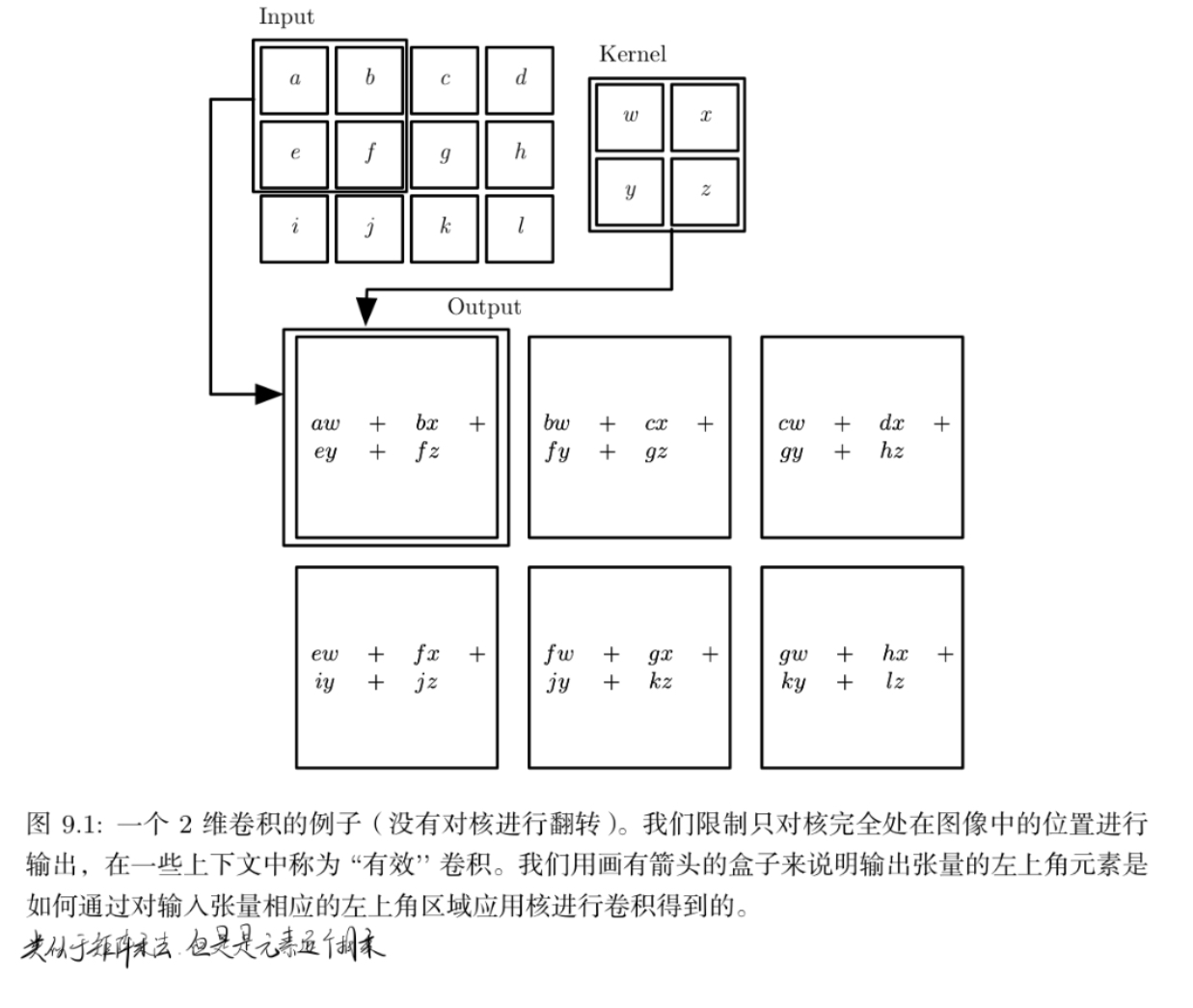
在卷积网络的术语中，卷积的第一个参数（在这个例子中，函数 x）通常叫做输入，第二个参数（函数 w）叫做核函数。输出有时被称作特征映射。

该式子可看作是把一个函数“翻转”并移位x时，测量f和K之间的重叠，并且体现了平移不变性和局部性：i，j发生变化时，卷积核并没有发生变化，同时收集i,j周围相关的信息时，只与较小范围（m,n）内的数据有关

卷积运算可交换性的出现是因为我们将核相对输入进行了翻转，从 m 增大的角度来看，输入的索引在增大，但是核的索引在减小。
许多神经网络库实际上是通过实现互相关函数来代替

\[S(i,j) = (I * K)(i,j) = \sum_m \sum_n I(i+m, j+n) K(m,n) \]

和卷积运算几乎一样但是并没有对核进行翻转（也就是相差一个负号）

动机

卷积运算通过三个重要的思想来帮助改进机器学习系统： 稀疏交互、 参数共享、 等变表示

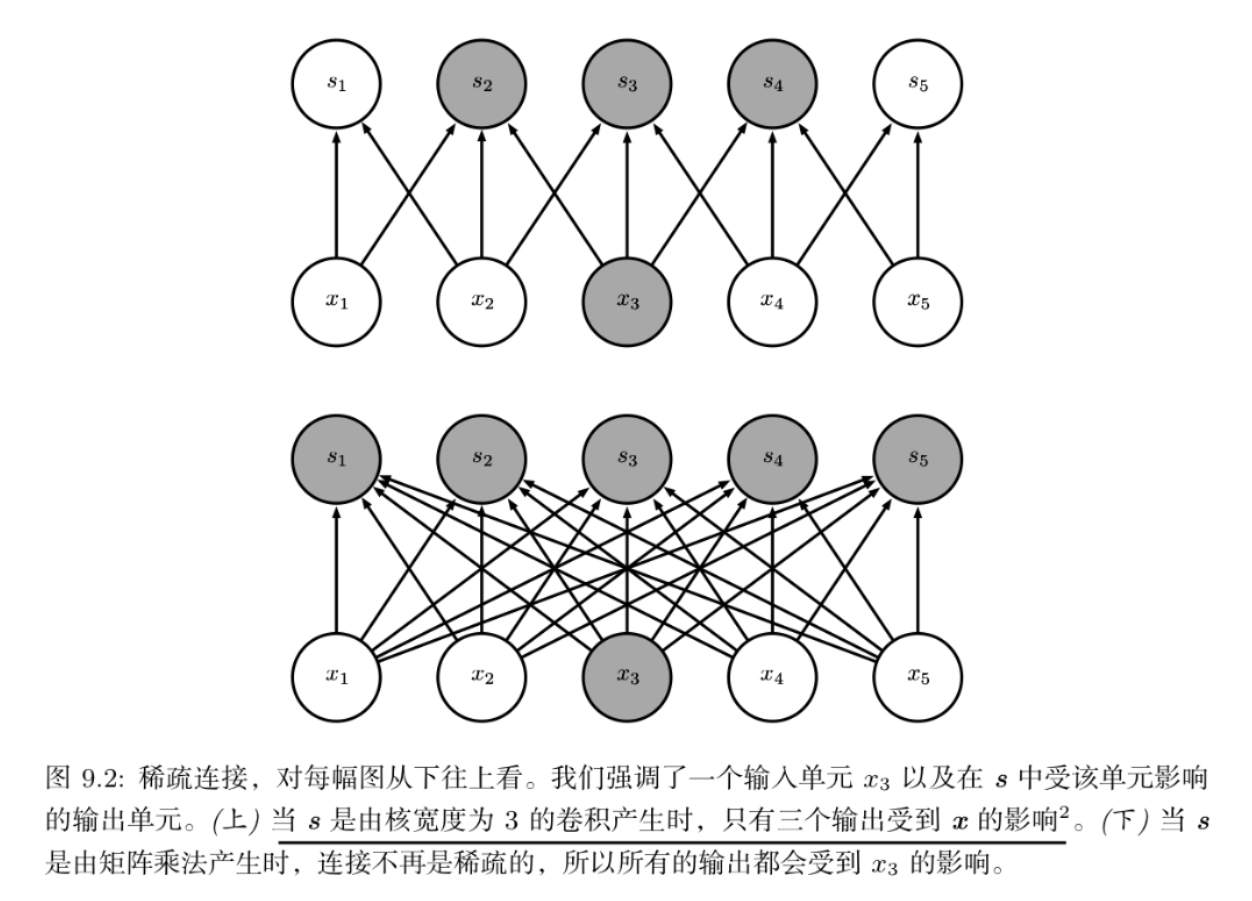
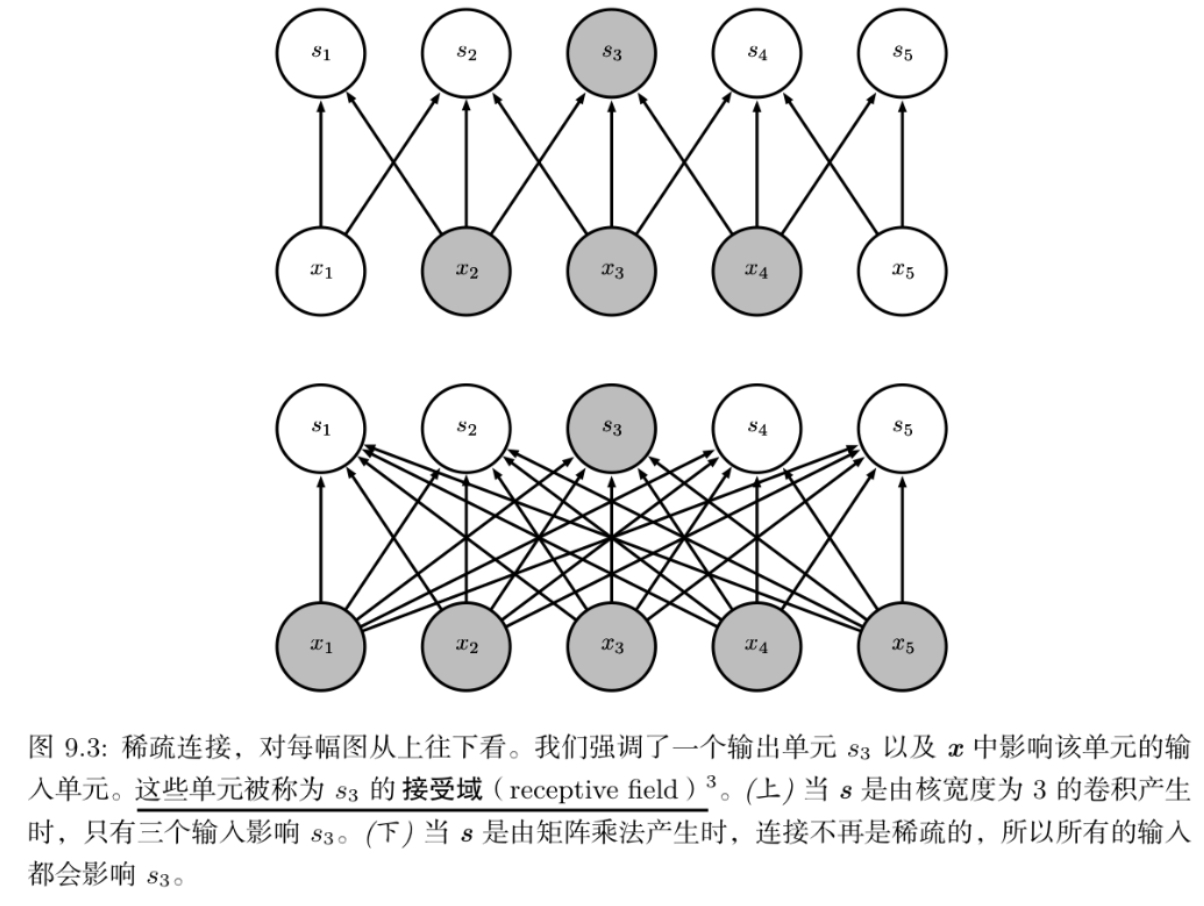
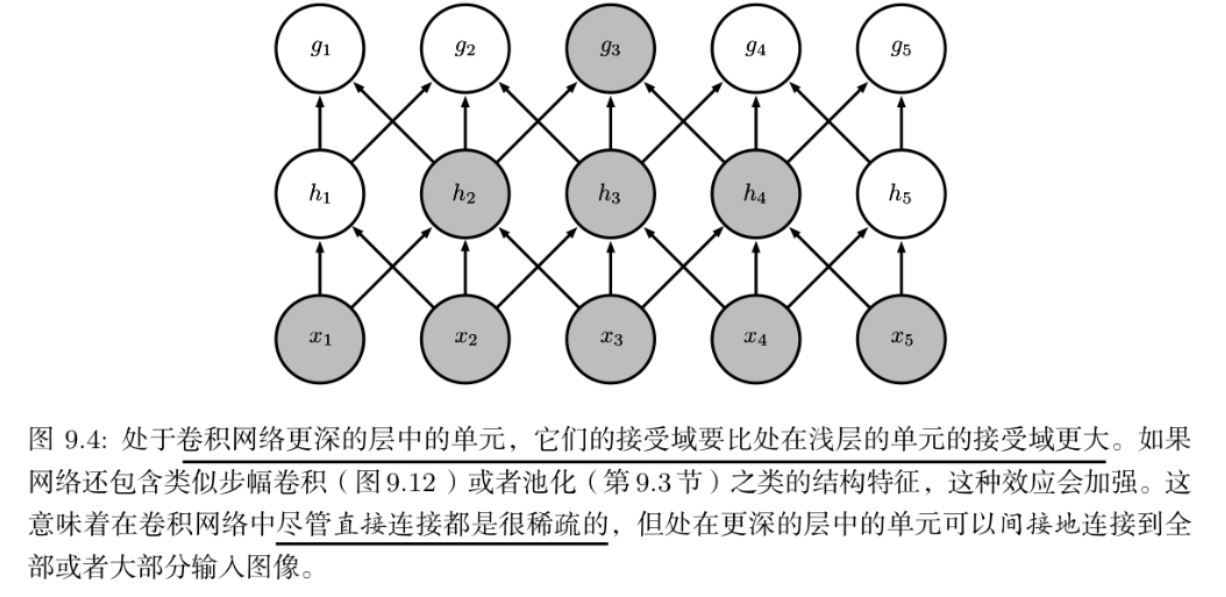
稀疏交互

参数矩阵中的每一个参数都描述了一个输入单元和一个输出单元之间的交互
卷积网络通过使核的大小远小于输入的大小来实现稀疏交互

参数共享

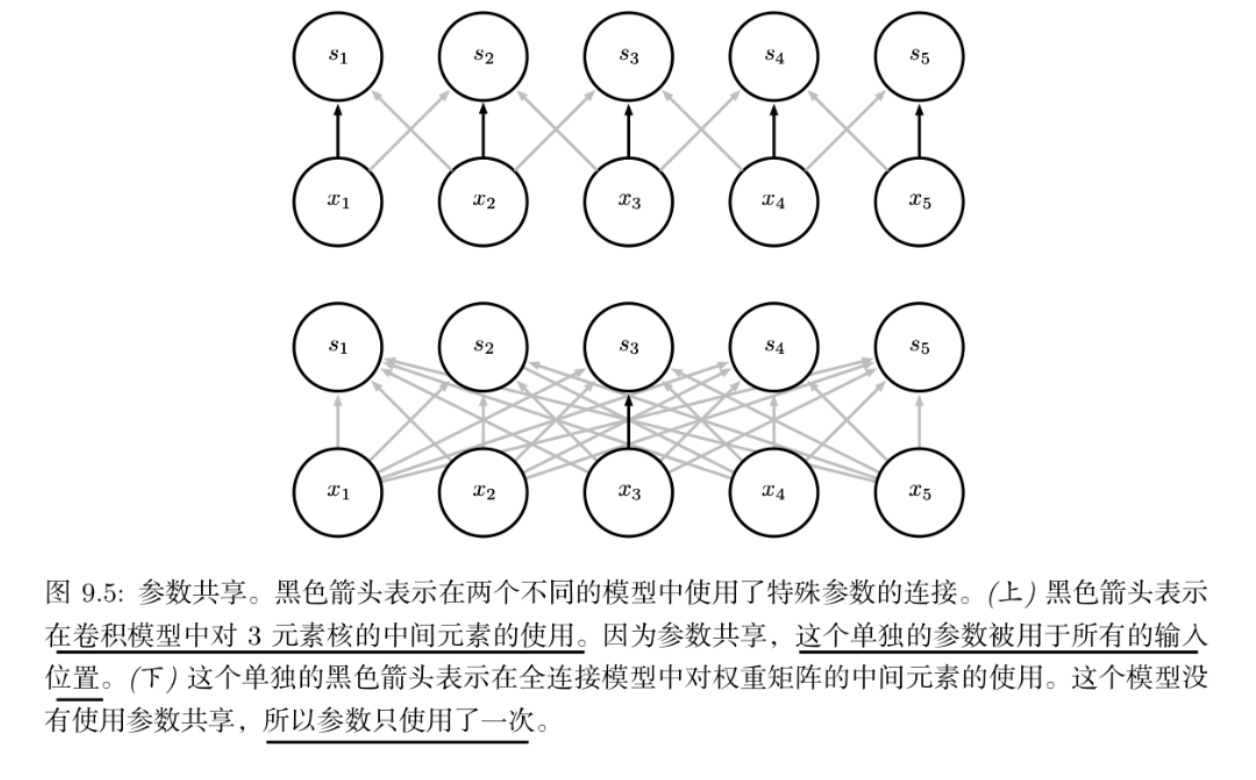
是指在一个模型的多个函数中使用相同的参数。 在传统的神经网络中，当计算一层的输出时，权重矩阵的每一个元素只使用一次
而在卷积神经网络中，核的每一个元素都作用在输入的每一位置上（是 否考虑边界像素取决于对边界决策的设计）。卷积运算中的参数共享保证了我们只需 要学习一个参数集合，而不是对于每一位置都需要学习一个单独的参数集合。

等变表示

对于卷积，参数共享的特殊形式使得神经网络层具有对平移 等变的性质。
如果一个函数满足输入改变，输出也以同样的方式改变这一性质，我们就说它是等变的。特别地，如果函数 f(x) 与 g(x) 满足 f(g(x)) = g(f(x))， 我们就说 f(x) 对于变换 g 具有等变性。
对于卷积来说，如果令 g 是输入的任意平移函数，那么卷积函数对于 g 具有等变性。

但对于其他的一些变换并不是天然等变的，例如图像的放缩或者旋转变换

池化

卷积网络中一个典型层包含三级。
在第一级中，这一层并行地计算多个卷积产生一组线性激活响应。在第二级中，每一个线性激活响应将会通过一个 非线性的激活函数，例如整流线性激活函数。这一级有时也被称为探测级。在第三级中，我们使用池化函数来进一步调整这一层的输出。

池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出
同时，不管采用什么样的池化函数，当输入作出少量平移时，池化能够帮助输入的表示近似不变；因此，使用池化可以看作是增加了无线强的先验：这一层学得的函数必须具有对少量平移的不变性
局部平移不变性是一个很有用的性质，尤其是当我们关心某个特征是否出现而不关心它出现的具体位置时。