概率图模型

机器学习最重要的任务，是根据一些已观察到的证据（例如训练样本）来对感兴趣的未知变量（例如类别标记）进行估计和推测。概率模型提供了一种描述框架，将学习任务归结于计算变量的概率分布。

在概率模型中，利用已知变量推测未知变量的分布称为“推断”，其核心是如何基于可观测变量推测出未知变量的条件分布.

• 监督学习（如 SVM）：
  目标：学习输入到输出的映射关系。
  实现：直接从数据到标签的映射。
  优点：简单高效，适用于标签明确的任务。
• 推断学习：
  目标：通过隐变量解释观测数据的生成过程。
  实现：建模观测数据和隐变量之间的关系。
  优点：能够解释数据的内在结构，处理不确定性。
  在存在隐变量的情况下，通过观测数据推断隐变量的分布或状态。
  通过隐变量来解释观测数据

最终目的都是由已知数据来得到一些类似于分类模型的概念

概率图模型是一类用图来表达变量相关关系的概率模型，图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”
根据边的性质不同，概率图模型可大致分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网

若变量间存在显式的因果关系，则常使用贝叶斯网；若变量存在相关性，但难以获得显式的因果关系，则常使用马尔可夫网

隐马尔可夫模型(HMM)

HMM是结构最简单的动态贝叶斯网，是一种有向图模型
隐马尔可夫模型中的变量可分为两组，第一组是状态变量\({y_1,y_2,\ldots,y_n}\)，其中\(y_i\)表示第i时刻的系统状态，一般假定状态变量是隐藏的、不可观测的，因此状态变量又称隐变量，同时状态变量\(y_i\)的取值范围\mathcal{Y}，称为状态空间，通常是有N个可能取值的离散空间；第二组是观测变量\({x_1,x_2,\ldots,x_n}\)，其中\(x_i\)表示第i时刻的观测值

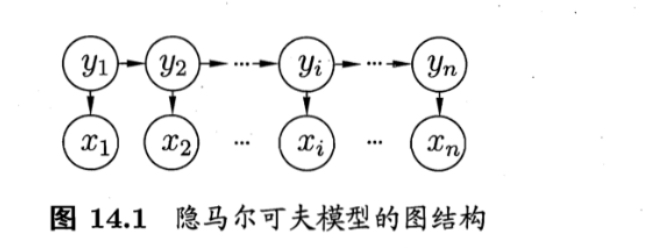
隐马尔可夫模型中，观测变量的取值仅依赖于状态变量，即\(x_i\)唯一由\(y_i\)决定，同时，\(y_t\)仅依赖于\(y_{t-1}\)，即系统下一时刻的状态仅由当前状态状态决定，基于这种依赖关系，所有变量的联合概率分布为$P(x_1, y_1, \ldots, x_n, y_n) = P(y_1) P(x_1 \mid y_1) \prod_{i=2}^{n} P(y_i \mid y_{i-1}) P(x_i \mid y_i) $
以上的是图结构相关的信息，但依据概率分布公式也可以得到，确定一个隐马尔可夫模型还需要如下三组参数：状态转移概率、输出观测概率以及初始状态概率

隐马尔可夫模型的三个基本问题是：
评估问题：计算观测序列的概率，使用前向算法或后向算法。
解码问题：找到最优的隐状态序列，使用维特比算法。
学习问题：估计模型参数，使用Baum-Welch算法。

评估问题与学习问题的区别
目标不同：
评估问题：计算给定模型下得到当前观测序列的概率。
学习问题：估计模型参数，使得观测序列的似然度最大化。
应用场景不同：
评估问题：用于模型评估、序列分类或比较不同模型的拟合程度。
学习问题：用于从数据中训练隐马尔可夫模型，是模型构建阶段的核心任务。

马尔可夫随机场

MRF是典型的马尔可夫网，是一种无向图模型
马尔可夫随机场有一组势函数，亦称因子，这是定义在变量子集上的非负实函数，主要用于定义概率分布模型

在马尔可夫随机场中，对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个“团” . 若在一个团中加入另外任何一个结点都不再形成团，则称该团为“极大团”；换言之，极大团就是不能被其他团所包含的团。也就是图论中的连通分量概念

每个结点至少出现在一个极大团中

在马尔可夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关。具体来说，对于 \(n\) 个变量 \(\mathbf{x} = \{x_1, x_2, \ldots, x_n\}\)，所有团构成的集合为 \(\mathcal{C}\)，与团 \(Q \in \mathcal{C}\) 对应的变量集合记为 \(\mathbf{x}_Q\)，则联合概率 \(P(\mathbf{x})\) 定义为

$ P(\mathbf{x}) = \frac{1}{Z} \prod_{Q \in \mathcal{C}} \psi_Q(\mathbf{x}_Q) $

其中 \(\psi_Q\) 为与团 \(Q\) 对应的势函数，用于对团 \(Q\) 中的变量关系进行建模，\(Z = \sum_{\mathbf{x}} \prod_{Q \in \mathcal{C}} \psi_Q(\mathbf{x}_Q)\) 为规范化因子，以确保 \(P(\mathbf{x})\) 是被正确定义的概率。在实际应用中，精确计算 \(Z\) 通常很困难，但许多任务往往并不需获得 \(Z\) 的精确值。

势函数量化团内变量的相容性或亲和度（密切度），值越大表示该配置越可能，也就是将团中的变量取值集合映射到一个非负值上

显然，若变量个数较多，则团的数目将会很多(例如，所有相互连接的两个变量都会构成团)，这就意味着上式会有很多乘积项，显然会给计算带来负担。注意到若团 \(Q\) 不是极大团，则它必被一个极大团 \(Q^*\) 所包含，即 \(\mathbf{x}_Q \subseteq \mathbf{x}_{Q^*}\)；这意味着变量 \(\mathbf{x}_Q\) 之间的关系不仅体现在势函数 \(\psi_Q\) 中，还体现在 \(\psi_{Q^*}\) 中。于是，联合概率 \(P(\mathbf{x})\) 可基于极大团来定义。假定所有极大团构成的集合为 \(\mathcal{C}^*\)，则有

\(P(\mathbf{x}) = \frac{1}{Z^*} \prod_{Q \in \mathcal{C}^*} \psi_Q(\mathbf{x}_Q)\)

因子并不是定义在节点上，而是定义在变量子集（团）上的，因为极大团保证了是唯一且独立的，因此可以确保每个因子仅与一个（极大）团相关
于是，相当于对联合概率分布对应的图进行最大连通分量分解，基于这个分解结果和因子来计算

马尔可夫随机场中的条件独立性

若从结点集 A中的结点到B中的结点都必须经过结点集C中的结点，则称结点集 A和B被结点集C分离，C称为“分离集”
对马尔可夫随机场，有

• 全局马尔可夫性：给定两个变量子集的分离集，则这两个变量子集条件独立

由此有两个推论：

• 局部马尔可夫性: 给定某变量的邻接变量，则该变量条件独立于其他变量。形式化地说，令 \(V\) 为图的结点集，\(n(v)\) 为结点 \(v\) 在图上的邻接结点，\(n^*(v) = n(v) \cup \{v\}\)，有 \(\mathbf{x}_v \perp \mathbf{x}_{V \setminus n^*(v)} \mid \mathbf{x}_{n(v)}\)。

• 成对马尔可夫性: 给定所有其他变量，两个非邻接变量条件独立。形式化地说，令图的结点集和边集分别为 \(V\) 和 \(E\)，对图中的两个结点 \(u\) 和 \(v\)，若 \(\langle u, v \rangle \notin E\)，则 \(\mathbf{x}_u \perp \mathbf{x}_v \mid \mathbf{x}_{V \setminus \{u, v\}}\)。
  （整个马尔可夫随机场保证了连通性，因此如果两个节点之间没有连边，那么这两个节点一定是相互独立的）

条件随机场

CRF是一种判别式无向图模型
前两种方法都是生成式模型，也就是直接对联合分布进行建模，而判别式模型则是对条件分布进行建模

条件随机场试图对多个变量在给定观测值后对条件概率进行建模，可以看作是给定观测值的马尔可夫随机场
因此，类似地，条件随机场也使用团上的势函数来定义概率
MRF：建模的是变量之间的联合概率分布 P(Y)，其中 Y 是所有随机变量的集合。它通过无向图表示变量之间的依赖关系，并假设每个变量在其邻居的条件下与其他变量独立。
CRF：建模的是给定观测序列 X 时，标签序列 Y 的条件概率分布 P(Y|X)。它同样使用无向图来表示标签之间的依赖关系，但这种依赖关系是在观测序列 X 的条件下建立的。