聚类学习
无监督学习中,训练样本的标记信息是位置的,这时就需要通过对无标记训练样本的学习来揭示数据的内在性质及规律
聚类试图将数据集中的样本划分为若干个不相交的子集,每个子集称为一个“簇”
性能度量
判断怎么样的聚类结果是比较好的,显然,聚类结果的“簇内相似度”高且“簇间相似度”低
常用的聚类性能内部指标:
DB指数(DBI):\(\text{DBI} = \frac{1}{k} \sum_{i=1}^{k} \max_{j \neq i} \left( \frac{\text{avg}(C_i) + \text{avg}(C_j)}{d_{\text{cen}}(\mu_i, \mu_j)} \right)\)
Dunn指数(DI):\(\text{DI} = \min_{1 \leq i \leq k} \left\{ \min_{j \neq i} \left( \frac{d_{\min}(C_i, C_j)}{\max_{1 \leq l \leq k} \text{diam}(C_l)} \right) \right\}\)
(\(d_{cen}\)是两个簇中心点之间的距离,\(d_{min}\)是两个簇的最近样本距离,diam是簇中样本间的最远距离)
显然,DBI的值越小越好,DI的值越大越好
距离
以上这些指标都依赖于距离的计算
对于函数\(dist(\cdot,\cdot)\),如果它是一个距离度量,则需满足一些基本性质:
-
非负性:$\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) \geq 0$
-
同一性:\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) = 0\) 当且仅当 $\boldsymbol{x}_i = \boldsymbol{x}_j$
-
对称性:$\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \text{dist}(\boldsymbol{x}_j, \boldsymbol{x}_i)$
-
直递性:\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) \leq \text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_k) + \text{dist}(\boldsymbol{x}_k, \boldsymbol{x}_j)\)
最常用的距离是闵可夫斯基距离
对于连续型数据和具有“序”关系的离散数据,距离计算是容易的
对于无序的离散属性可以用VDM
原型聚类
原型聚类假设聚类结构能通过一组原型刻画,原型是指样本空间中具有代表性的点
通常情况下,算法先对原型进行初始化,然后对原型进行迭代更新求解
k均值算法
k-means针对聚类得到的簇划分,最小化平方误差\(E = \sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_i} \|\boldsymbol{x} - \boldsymbol{\mu}_i\|_2^2 \tag{9.24}\)
其中\(\boldsymbol{\mu}_i\)是簇\(C_i\)的均值向量
k-means通过如下算法进行计算

学习向量量化(LVQ)
LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类
这也是LVQ和k-means,即LVQ实际上是一个监督模型,通过迭代调整原型向量的位置,得到的是一个分类模型
LVQ的目标是学得一组原型向量,每个向量代表一个聚类簇

关键是关于如何更新原型向量,直观上看,对样本\(\boldsymbol{\x_j}\),若最近的原型向量\(\boldsymbol{\p_i*}\)与\(\boldsymbol{\x_j}\)的类别标记相同,则令\(\boldsymbol{\p_i*}\)向\(\boldsymbol{\x_j}\)的方向靠拢
每个原型向量\(\boldsymbol{\p_i}\)定义了与之相关的一个区域,该区域中每个样本与\(\boldsymbol{\p_i}\)的距离不大于与其他原型向量的距离,由此形成了对于样本空间的划分
高斯混合聚类
采用概率模型来表达聚类模型(本质是个生成模型,学习了训练集的样本分布)
我们可定义高斯混合分布
\(p_{\mathcal{M}}(\boldsymbol{x}) = \sum_{i=1}^{k} \alpha_i \cdot p(\boldsymbol{x} \mid \boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i), \tag{9.29}\)
\(p_{\mathcal{M}}(\cdot)\) 也是概率密度函数,\(\int p_{\mathcal{M}}(\boldsymbol{x}) \mathrm{d}\boldsymbol{x} = 1\)。
该分布共由k个混合成分组成,每个混合成分对应一个高斯分布。其中 \(\boldsymbol{\mu}_i\) 与 \(\boldsymbol{\Sigma}_i\) 是第 i个高斯混合成分的参数,而 \(\alpha_i > 0\)为相应的“混合系数”,\(\sum_{i=1}^{k} \alpha_i = 1\)
假设样本的生成过程由高斯混合分布给出:首先,根据\(\alpha_1, \alpha_2, \ldots, \alpha_k\)定义的先验分布选择高斯混合成分,其中\(\alpha_i\)为选择第 i个混合成分的概率;然后,根据被选择的混合成分的概率密度函数进行采样,从而生成相应的样本。
然后可以通过贝叶斯定理计算得到\(p_{\mathcal{M}}(z_j=j \mid \boldsymbol{x}_j)\),代表样本\(\boldsymbol{x_j}\)由第i个高斯混合成分生成的后验概率
从原型聚类的角度看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分由原型对应后验概率确定
模型参数的学习通过最大化数据的似然函数得到,采用EM算法:每步迭代,先根据当前参数计算每个样本属于每个高斯成分的后验概率,再根据相关式子更新模型参数

密度聚类(DBSCAN)
假设聚类结构能通过样本分布的紧密程度确定,在通常情形下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接和样本不断扩展聚类簇以获得最终的聚类结果

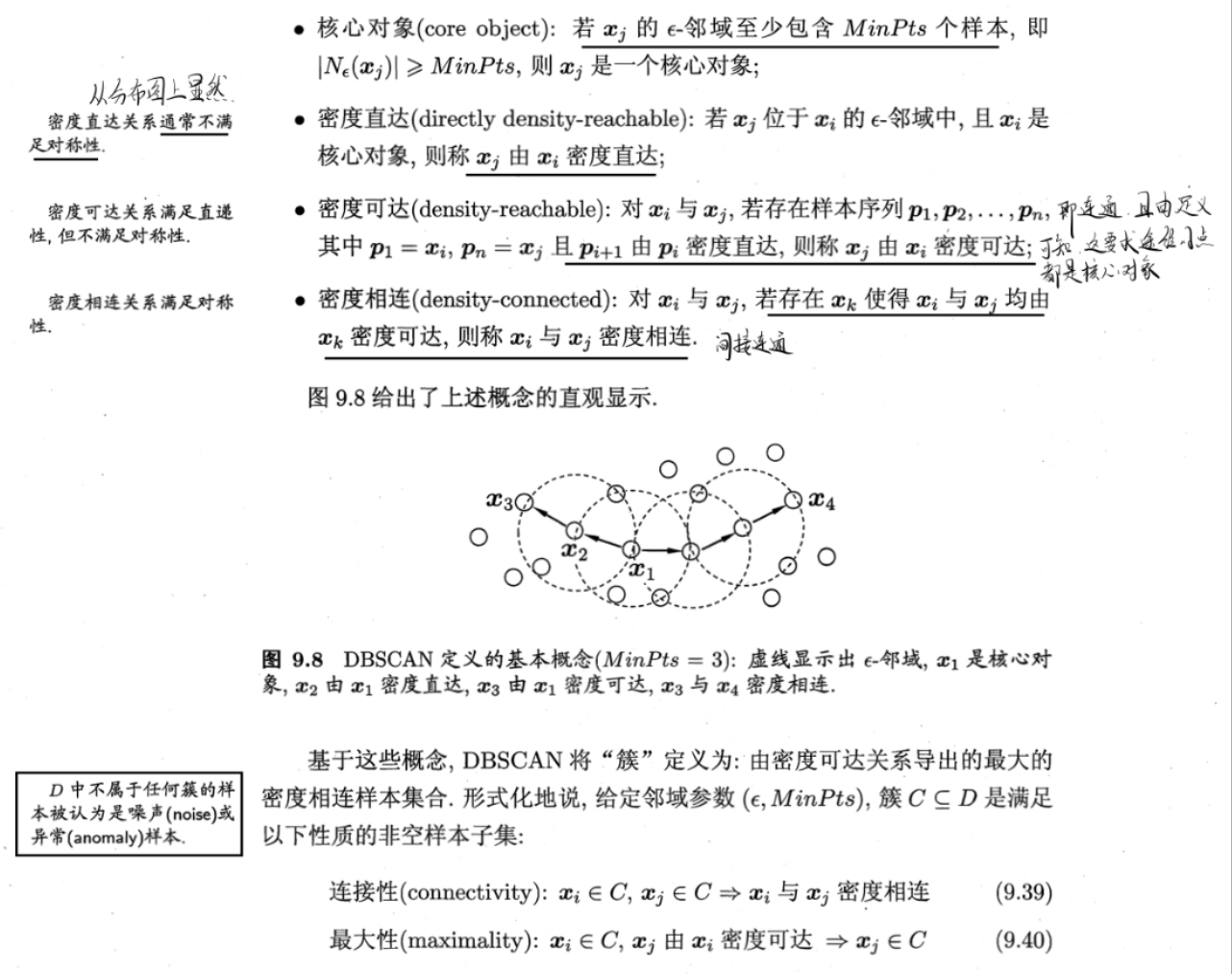
具体算法:


层次聚类
AGNES 是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中内每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数.这里的关
在不同层次对数据集进行划分,从而形成树形的聚类结构





 浙公网安备 33010602011771号
浙公网安备 33010602011771号