正则化

正则化个人认为是一些传统机器学习中最为核心的一个概念，它提供了一种形式去表示算法设计者对于目标模型形式的偏好，或者对模型进行一定的约束

表示对函数的偏好是比增减假设空间的成员函数更一般的控制模型容量的方法

具体来说，正则化项给目标函数添加了一个额外的惩罚项，使得参数在学习的过程中，强制在正则化项描述的形式周围进行学习，从而使得学得的模型具有某一特征
例如通过添加一个与模型复杂度成正比的惩罚项来避免学习的模型过于复杂，间接防止过拟合

岭回归

对于线性回归模型，如果使用\(L_2\)范数正则化，则有\(\min \limits_{\mathbf{w}} \sum_{i=1}^{m} (y_i - \mathbf{w}^{\mathrm{T}} \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_2^2\)，其中正则化参数\(\lambda > 0\)，通过引入\(L_2\)范数正则化，能显著降低过拟合风险
该正则化也被称为权重衰减

如果采用\(L_1\)来进行正则化，那么有\(\min \limits_{\mathbf{w}} \sum_{i=1}^{m} (y_i - \mathbf{w}^{\mathrm{T}} \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_1^2\)，该式又称为LASSO
同时，使用\(L_1\)正则化，更容易得到稀疏解，也就是它求得的\(\mathbf{w}\)有更少的非零分量

在深度学习的背景下，大多数正则化策略都会对估计进行正则化，估计的正则化以偏差的增加换取方差的减小，自然我们期望能显著减小方差而不过度增加偏差

在讨论泛化和过拟合时，主要侧重模型族训练的3个情形（模型的训练结果）：
（1）不包括真实的数据生成过程——对应欠拟合和含有偏差的情况（欠拟合，偏差主导）
（2）匹配真实数据生成过程（最佳拟合）
（3）除了包括真实的数据生成过程，还包 括许多其他可能的生成过程——方差（而不是偏差）主导的过拟合。（包括其他生成过程是指将例如噪声也进行了拟合）
正则化的目标是使模型从第三种情况转化为第二种情况。

参数范数惩罚

\(\tilde{J}(\theta; \mathbf{X}, y) = J(\theta; \mathbf{X}, y) + \alpha \Omega(\theta)\)
此时使用训练算法最小化正则化后的目标函数时，会降低原始目标 J 关于训练数据的误差并同时减小在某些衡量标准下参数 θ（或参数子集）的规模

在神经网络中，参数包括每一层仿射变换的权重和偏置，我们通常只对权重做惩罚而不对偏置做正则惩罚

作为约束的范数惩罚

在使用广义拉格朗日函数来最小化带约束的函数时，会在原始目标函数上添加一系列惩罚项，每个惩罚是一个被称为KKT乘子的系数以及一个表示约束是否满足的函数之间的乘积，例如想约束\(\Omega(\theta)\)小于某个常数k，则可以构建广义拉格朗日函数

\[\mathcal{L}(\theta, \alpha; \mathbf{X}, y) = J(\theta; \mathbf{X}, y) + \alpha (\Omega(\theta) - k). \]

解决这个问题我们需要对\(\theta\)和\(\alpha\)都做出调整。虽然有许多不同的优化方法，但在所有过程中 \(\alpha\) 在\(\Omega(\theta) > k\)时必须增加，在 \(\Omega(\theta) < k\)时必须减小。所有正值的 \(\alpha\)都鼓励\(\Omega(\theta)\)收缩（因为\(\alpha\)大于0）。最优值 \(\alpha^*\)也将鼓励\(\Omega(\theta)\)收缩，但不会强到使得\(\Omega(\theta)\)小于\(k\)。
直观地看，较大的\(\alpha\)将得到一个较小的约束区域，而较小的\(\alpha\)将得到一个较大的约束区域

Dropout

Dropout提供了正则化一大类模型的方法
Dropout是一种简单而有效的正则化技术，通过在训练过程中随机丢弃神经元，防止模型过拟合并增强其泛化能力。它的核心思想是减少神经元之间的复杂共适应性，迫使每个神经元独立地学习有用的特征。

Dropout可以被认为是集成大量深层神经网络的实用Bagging方法。Bagging涉及训练多个模型， 并在每个测试样本上评估多个模型。
而Dropout提供了一种廉价的Bagging集成近似，能够训练和评估指数级数量的神经网络。

具体而言，Bagging学习中， 我们定义 k 个不同的模型， 从训练集有放回采样构造 k 个不同的数据集，然后在训练集 i 上训练模型 i。Dropout的目标是在指数级数量的神经网络上近似这个过程。

Dropout训练的集成包括所有从基础网络中除去非输出单元后形成的子网络，例如：

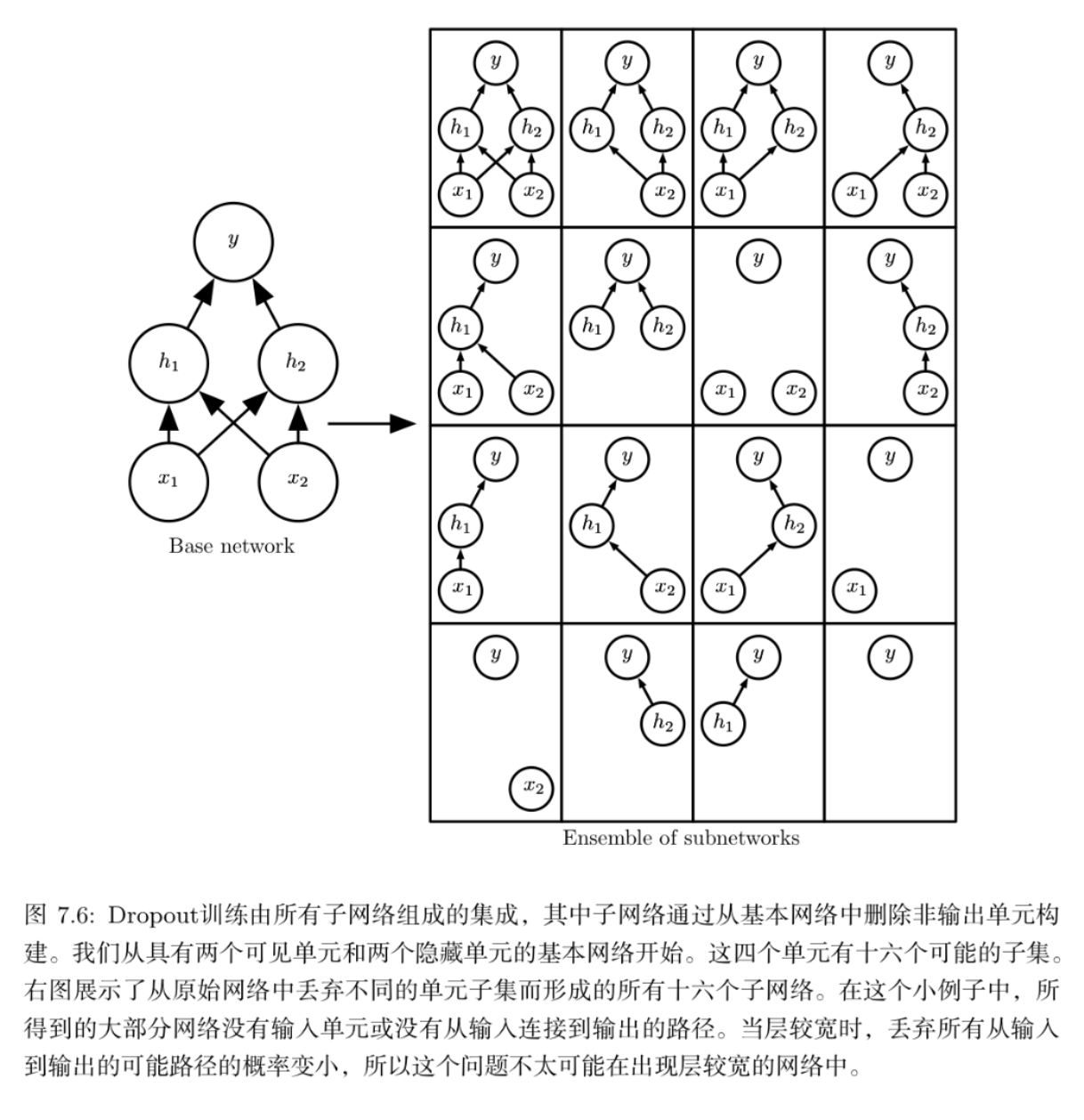
假设一个掩码向量\(\mu\)指定被包括的单元，\(J(\theta, \mu)\)是由参数\(\theta\)和掩码\(\mu\)定义的模型代价。那么Dropout训练的目标是最小化 \(\mathbb{E}_\mu J(\theta, \mu)\)。这个期望包含多达指数级的项，但可以通过抽样\(\mu\)获得梯度的无偏估计

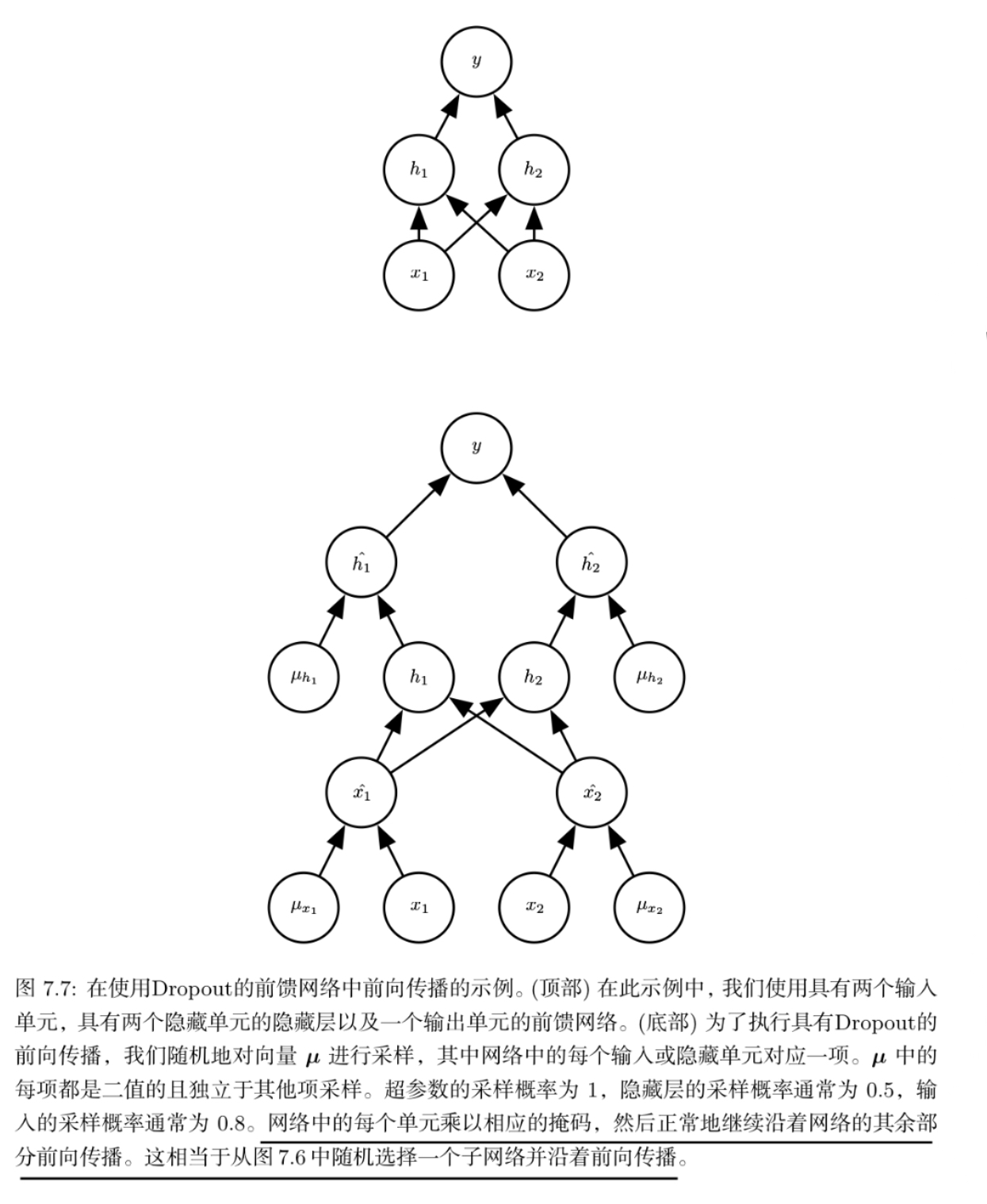
在Dropout的情况下， 所有模型共享参数， 其中每个模型继承父神经网络参数的不同子集。参数共享使得在有限可用的内存下表示指数级数量的模型变得可能。
虽然因为父神经网络会很大，以至于子网络的数量规模非常大，无法完成采样，但是通过在单个步骤中训练一小部分的子网络，参数共享会使得剩余的子网络也能有好的参数设定

同样，我们进行推断，并类似的需要采样近似推断，平均许多掩码的输出
一个更好的方法能不错地近似整个集成的预测，且只需一个前向传播的代价。要做到这一点，我们改用集成成员预测分布的几何平均而不是算术平均。

在训练阶段，Dropout以概率p随机丢弃神经元（即输出置零），而在测试阶段需要关闭Dropout以进行确定性预测。为了保持输出的期望值一致，通常需要对保留的神经元的权重进行比例缩放
多个概率分布的几何平均不能保证是一个概率分布。为了保证结果是一个概率分布，我们要求没有子模型给某一事件分配概率 0，并重新标准化所得分布。通过几何平均直接定义的非标准化概率分布由下式给出

\[\tilde{p}_{\text{ensemble}}(y \mid x) = \sqrt[2^d]{\prod_\mu p(y \mid x, \mu)} \]

其中\(d\)是可被丢弃的单元数。这里为简化介绍，我们使用均匀分布的\(\mu\)，但非均匀分布也是可以的。为了作出预测，我们必须重新标准化集成：

\[p_{\text{ensemble}}(y \mid x) = \frac{\tilde{p}_{\text{ensemble}}(y \mid x)}{\sum_{y'} \tilde{p}_{\text{ensemble}}(y' \mid x)}. \]

涉及Dropout的一个重要观点是，我们可以通过评估模型中\(p(y \mid x)\)来近似\(p_{\text{ensemble}}\)：该模型具有所有单元，但我们将单元\(i\)的输出的权重乘以单元\(i\)的被包含概率。这个修改的动机是得到从该单元输出的正确期望值。我们把这种方法称为权重比例推断规则

Dropout 的正则化效果主要来源于减少神经元之间的共适应性、模型集成效应和噪声注入，而这些机制并不完全依赖于随机性。虽然经典 Dropout 使用随机性来实现这些机制，但通过确定性丢弃、噪声注入或结构化 Dropout 等方法，同样可以实现类似的正则化效果。随机性在 Dropout 中的主要优势在于其简单性、多样性和无偏性，但它并不是实现正则化效果的必要条件。