机器学习概要

主要基于西瓜书、深度学习花书、统计学习方法

基于篇幅和实际应用，只打算侧重于整理概念之间的关系以及多本书内容的整合，不会过多设计推导以及一些更深的概念

作为对机器学习的一个初步认识，很多内容可能有不准确的地方

大多机器学习算法都是在利用梯度和学习率来进行更新，但是在梯度的计算以及具体利用梯度的什么形式上进行更新有很大的区别

统计学习是计算机基于数据构建概率统计模型并运用模型对数据进行预测和分析的一门学科

统计学习关于数据的基本假设是同类数据具有一定的统计规律性

统计学习的方法是基于数据构建概率模型从而对数据进行预测和分析，统计学习由监督学习、无监督学习和强化学习等组成
具体方法可以概括如下：从给定的、有限的、用于学习的训练数据集合出发，假设数据是独立同分布产生的；并且假设要学习的模型属于某个函数的集合，称为假设空间；应用某个评价准则，从假设空间中选取一个最优模型，使它对已知的训练数据及位置的测试数据在给定的评价准则下有最优的预测；最优模型的选取则由算法实现

于是，统计学习方法包括模型的假设空间、模型选择的准则以及模型学习的算法，称其为模型、策略和算法

基本分类

监督学习

从标注数据中学习预测模型的机器学习问题，本质是学习输入到输出的映射的统计规律

输入空间、特征空间和输出空间

通常输出空间远远小于输入空间

每个具体的输入是一个实例，通常由特征向量表示，所有特征向量存在的空间称为特征空间。特征空间中的每一维对应于一个特征

假设空间

监督学习的目的在于学习一个由输入到输出的映射，这一映射由模型来表示
模型属于由输入空间到输出空间的映射的集合，这个集合就是假设空间

问题的形式化

在监督学习中，假设训练数据与测试数据是依据联合概率分布P(X, Y)独立同分布产生的

无监督学习

无监督学习的本质是学习数据中的统计概率或者潜在结构，输入和输出空间可以是有限元的集合，也可以是欧式空间
模型可以实现对数据的聚类、降维或概率估计

强化学习

强化学习是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题

假设智能系统与环境的互动基于马尔可夫决策过程，智能系统观测到的是与环境互动得到的数据序列，那强化学习的本质就是学习最优的序贯决策

马尔可夫决策过程是指具有马尔可夫性，即下一个状态只依赖于前一个状态与动作；学习通常从一个具体的策略开始，通过搜索更优的策略进行

按模型分类

概率模型与非概率模型

在监督学习中，概率模型取条件概率分布形式 P(y|x) ，非概率模型取函数形式 y = f(x)；无监督学习中，x 是输入，z是输出，概率模型取条件概率分布形式 P(z | x) 或 P(x | z) ，非概率模型取函数形式 z = f(x)

在监督学习中，概率模型是生成模型，非概率模型是判别模型
生成模型需要对数据的分布做出假设，并基于这些假设进行参数估计；生成式模型试图通过建模数据的生成过程来理解数据的内在结构，可以生成新的数据样本
判别模型不假设数据的生乘过程，而是直接建模输出和输入之间的关系；判别式模型专注于区分不同类别的数据，而不应是建模数据的生成过程

常见的模型中，决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、高斯混合模型是概率模型；感知机、支持向量机、k近邻、AdaBoost、k均值以及神经网络是非概率模型

条件概率和函数形式可以相互转化，例如条件概率分布最大后得到函数，函数归一化后可以得到条件概率分布，因此概率模型和非概率模型的最主要区别在于模型的内部结构，概率模型一定可以表示为联合概率分布的形式，其中的变量表示输入、输出、隐变量甚至参数，而针对非概率模型则不一定存在这样的联合概率分布

概率模型的代表是概率图模型，如贝叶斯网络、马尔可夫随机场、条件随机场是概率图模型，其联合分布可以根据图的结构分解为因子乘积的形式

参数化模型与非参数化模型

参数化模型假设模型参数的维度固定，模型可以由有限维参数完全刻画；非参数模型假设模型参数的维度不固定或者说无穷大，随着训练数据量的增加而不断增大
如感知机、朴素贝叶斯、k均值等是参数化模型，而决策树、支持向量机、AdaBoost、k近邻等是非参数化模型

按算法分类

依据算法，可以分为在线学习和批量学习

在线学习每次接受一个样本，进行预测，之后学习模型；而批量学习一次接受所有数据，学习模型，之后进行预测
例如利用随机梯度下降的感知机学习算法是在线学习方法

策略

f(X)关于联合分布P(X, Y)的平均意义下的损失，称为风险函数或者期望损失
f(X)关于训练数据集的平均损失称为经验风险

当模型是条件概率分布、损失函数是对数损失函数时，经验风险最小化等价于极大似然估计

结构风险最小化是为了防止过拟合而提出的策略，结构风险最小化等价于正则化；结构风险在经验风险上加上表示模型复杂度的正则化项或者罚项
当模型是条件概率分布、损失函数是对数函数、模型复杂度由模型的先验概率表示时，结构风险最小化等价于最大后验概率估计

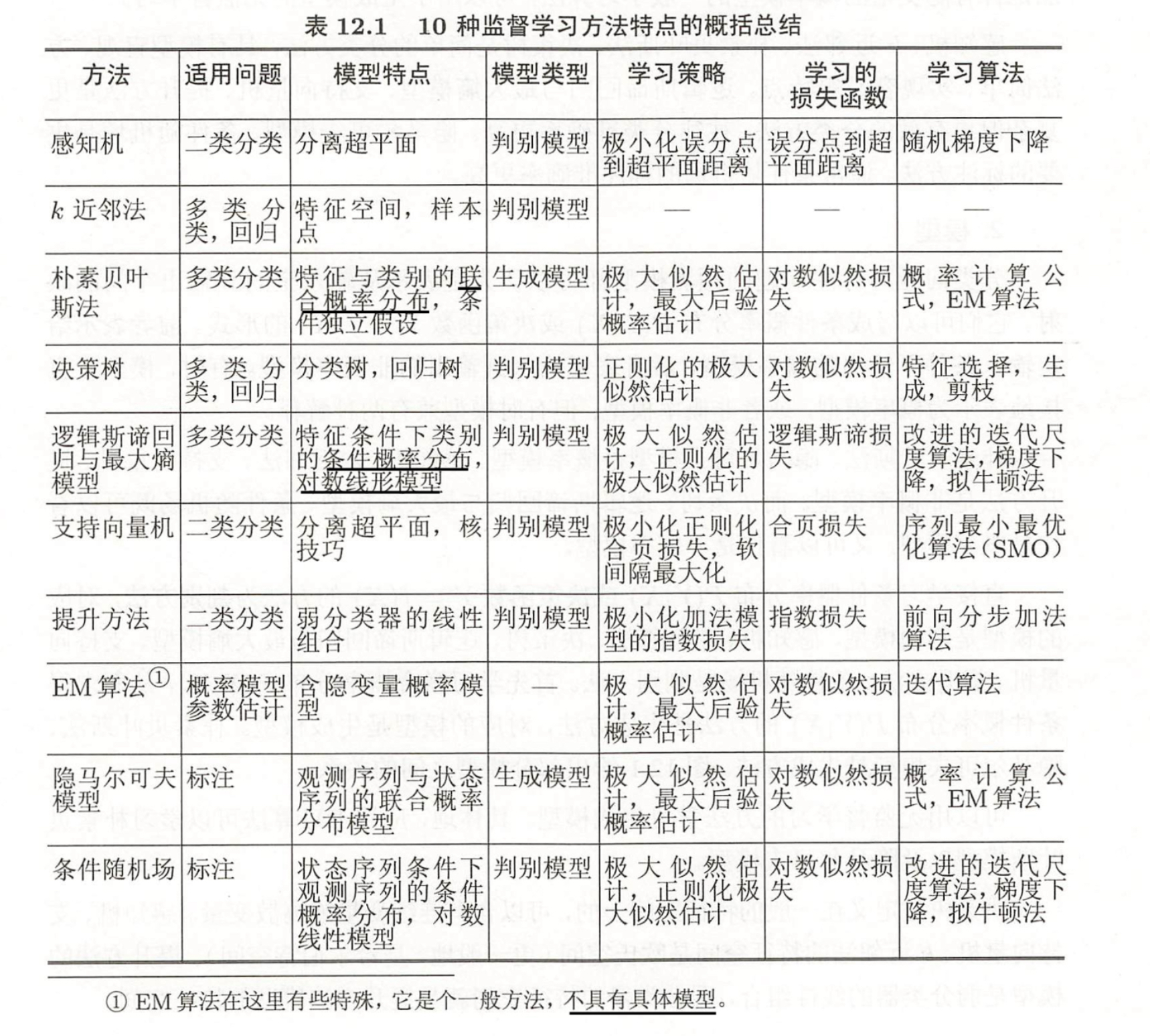
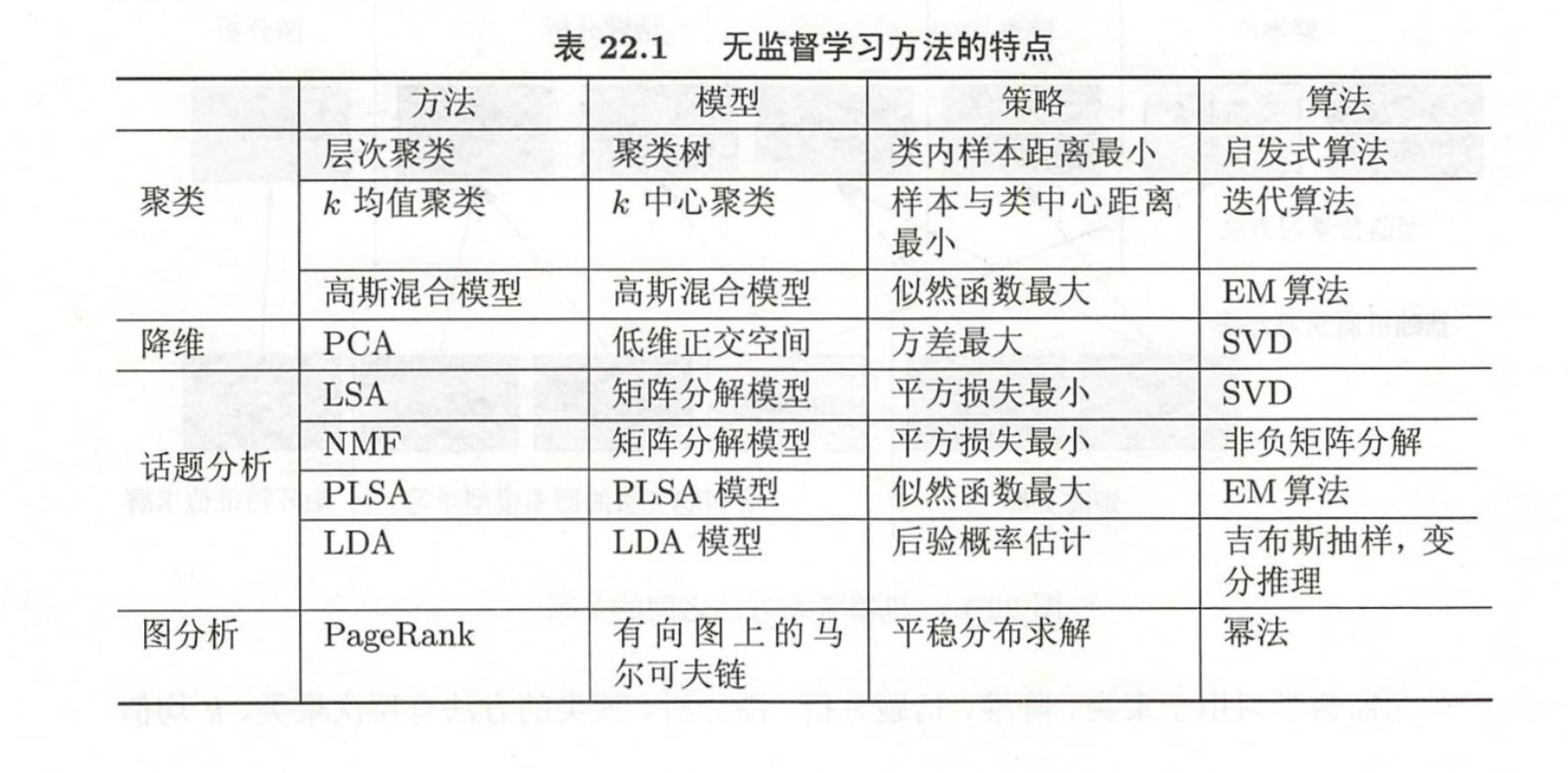
表格对比