一.数学
一.数学
第一章函数与极限
第一节映射与函数
一丶映射
二丶函数
函数的几种特性
有界性 单调性 奇偶性 周期性
三丶例题
第二节数列的极限
一丶数列极限的定义
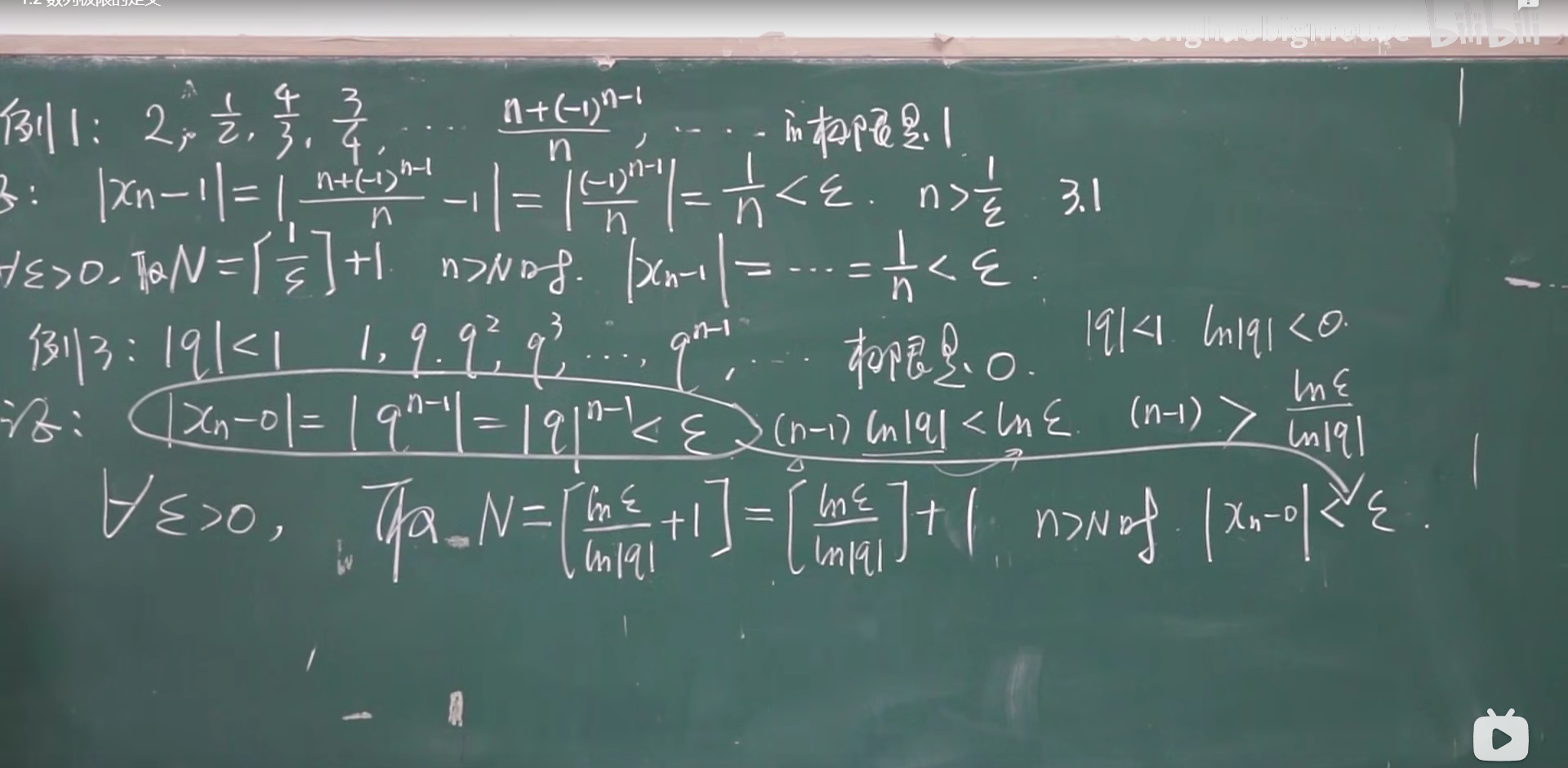
二丶收敛数列的性质
1.唯一性 极限唯一
2.有界性
如果数列收敛 那么一定有界 有界不一定收敛
3.保号性
4.如果数列收敛于a,那么它的任一子数列也收敛,且极限是a
如果数列x有两个子数列收敛于不同的极限,那么数列x是发散的
第三节 函数的极限
一丶函数极限的定义
求函数的极限时 自变量趋于某一个具体数值时 求δ 越小越好

左极限 右极限
1.x)极限存在充分必要条件是左右极限各自存在且相等

自变量趋于无穷大时的函数极限 求大X 越大越好
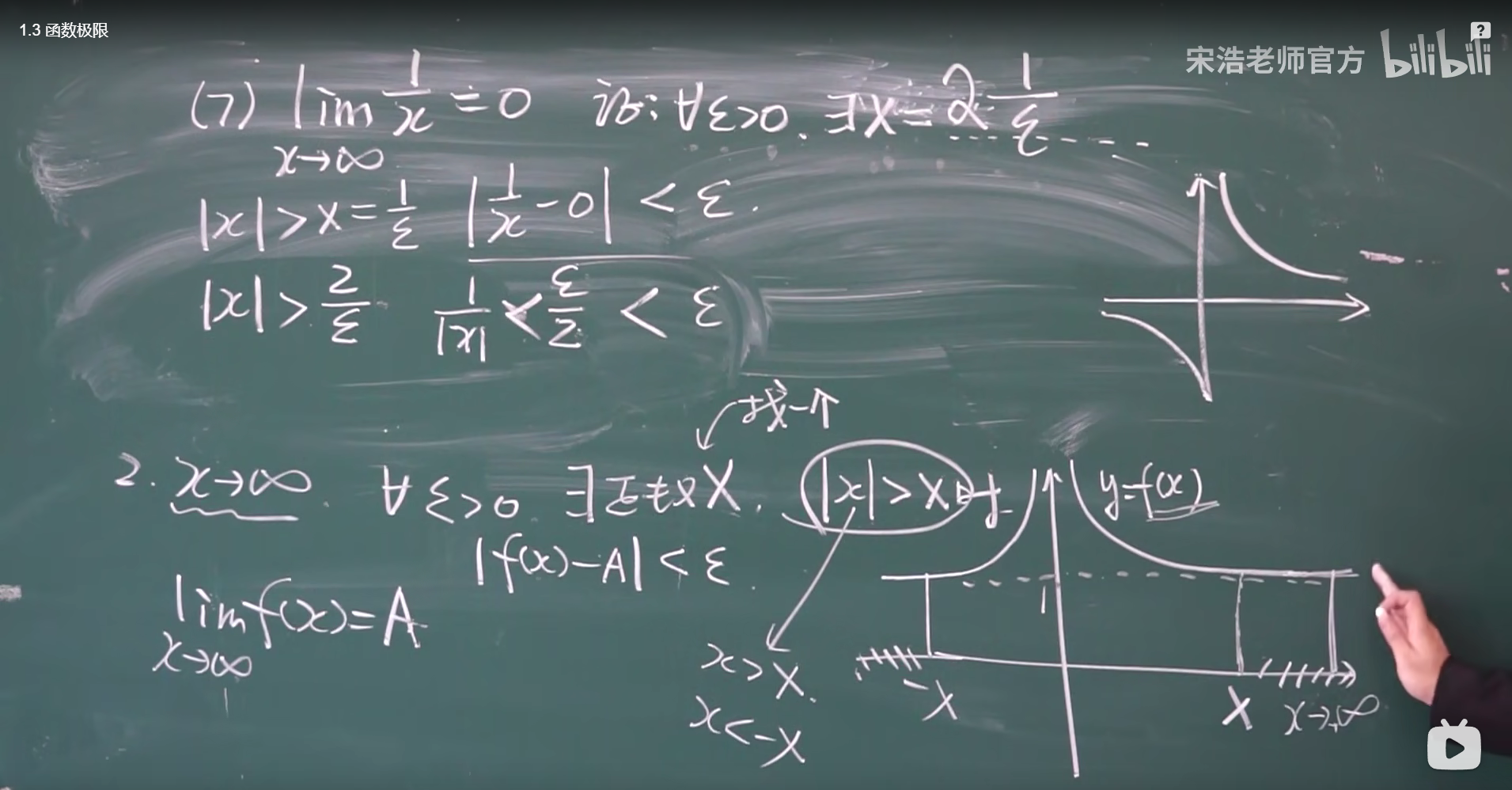
二丶函数极限的性质
定理1(函数极限的唯一性) 如果

定理4

三丶例题
第四节 无穷小与无穷大
一丶无穷小
除0以外的任何很小的常数都不是无穷小
无穷小指的是函数值趋于0
二丶无穷大
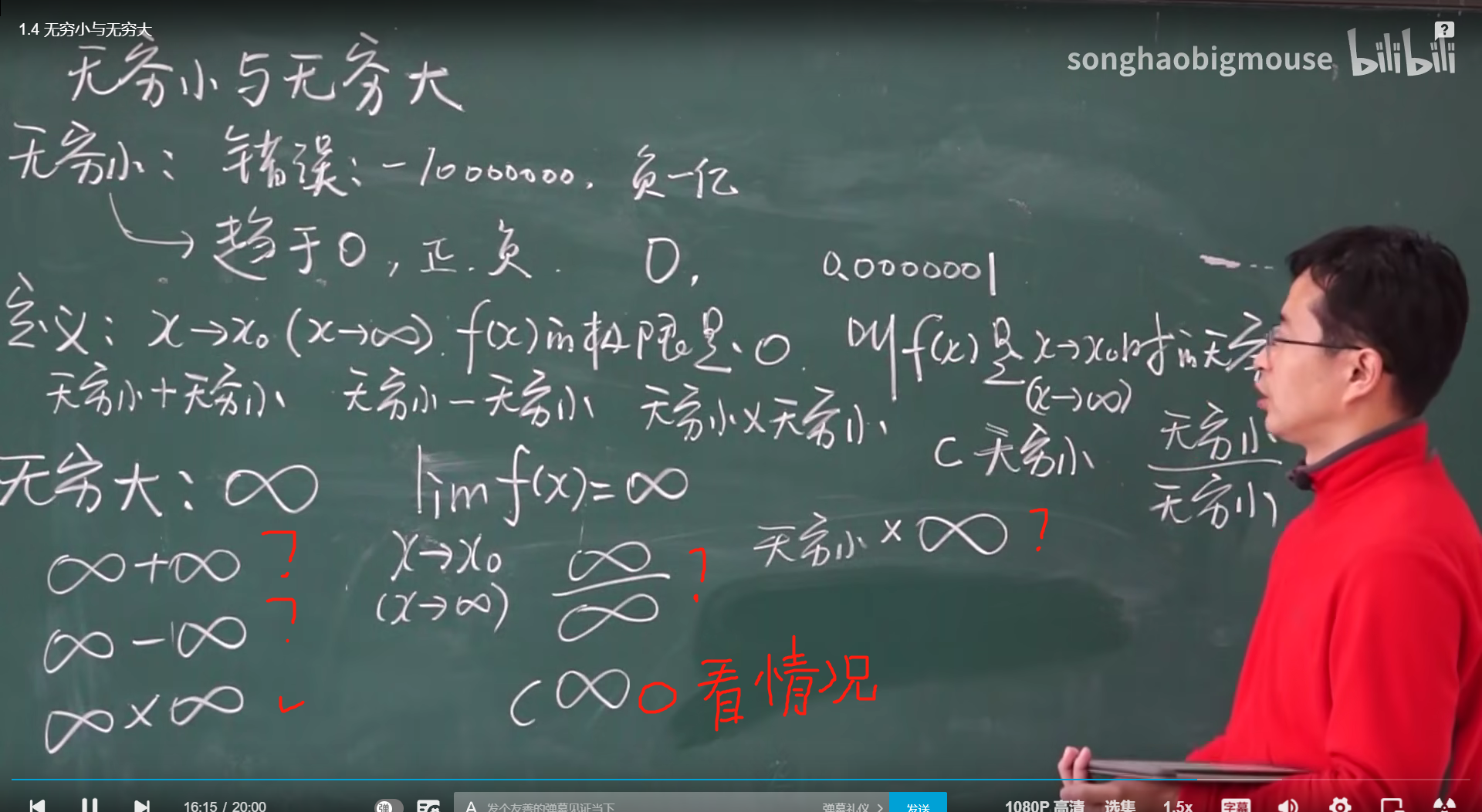

f(x)为无穷大,那么倒过来就是无穷小
f(x)为无穷小,那么倒过来就是无穷大 而且f(x)不等于0
第五节 极限运算法则
定理1 两个无穷小的和也是无穷小

有限个无穷小之和也是无穷小
无限个好像不一定
定理2 有界函数与无穷小的乘积是无穷小
有界函数比如说是 sin cos 等等
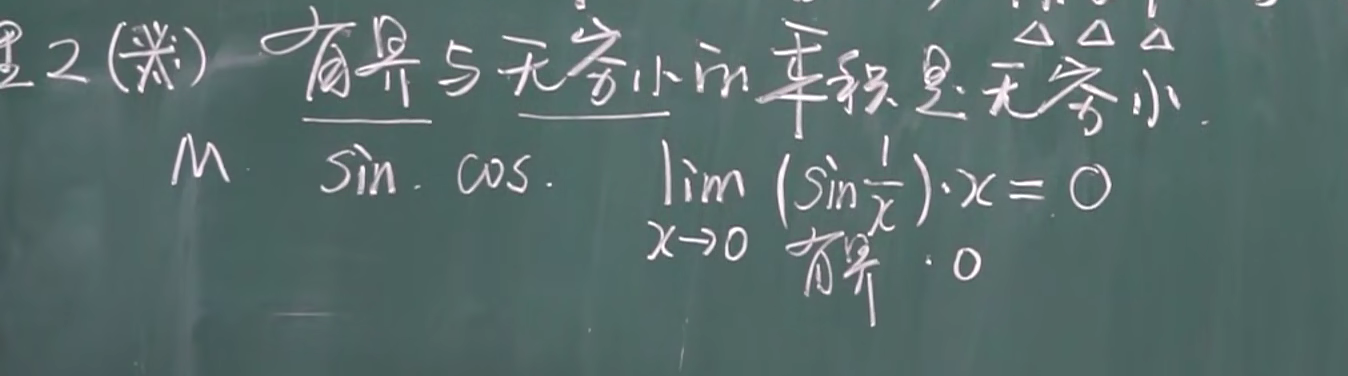
推论1 常数与无穷小的乘积是无穷小
推论2 有限个无穷小的乘积是无穷小

定理3 x都是趋于同一个极限的情况下

推论1 如果lim f(x)存在而c为常数,那么c可以往外提
推论2 如果lim f(x)存在而n是正整数,先求极限在n次方

定理4 同定理3差不多 把函数换成了数列
定理5 如果一个函数比另外一个函数大那么极限也比它大

极限运算的例题
例1代数 例二代数 例三因式分解代数 是0/0形态
例四 下面等于0所以等于无穷

例题五 分子分母除以x的最高次或者求导
例题六也是如此 下面还有一个不一样的思路解法 除以x平方 无穷大的倒数是无穷小
例题七一样
分母为0 无穷大
分子为0 无穷小=0

分子分母最高次
相等为一个常数
分子大为无穷大
分母大为无穷小=0

x趋于无穷的时候 才能用这个方法无穷小量分出法

定理6 复合函数就直接代数进去
极限的题型
1.直接代数
2.分解因式 和 求导代数 法
$$
\frac{0}{0}
$$
3.分子分母除以x的最高次 或者 求导代数
$$
\frac{\infty}{\infty}
$$
4.除以系数最大的 比如下面这题就是除以4
$$
lim_{x\rightarrow\infty}\frac{2n+3n}{3n+4n}
$$
第六节 极限存在准则 两个重要极限
1.夹逼准则
$$
g(x)\leq f(x)\leq h(x)
$$
$$
limg(x)=A
$$
$$
limh(x)=A
$$
那么
$$
limf(x)=A
$$

第一个重要极限
$$
lim_{x\rightarrow0}\frac{sinx}{x}=1
$$


第一个重要极限例题

上面用了sin(arcsinx)=x

2.单调有界数列必有极限
这里漏了第二个重要极限和柯西准则有空补回去
第七节 无穷小的比较
定义

等价证明

这里上面证明了下面这条式子 等价关系
$$
^n\sqrt{1+x}-1 \rightarrow\frac{1}{n}x
$$
两条定理

等价无穷小关系的应用
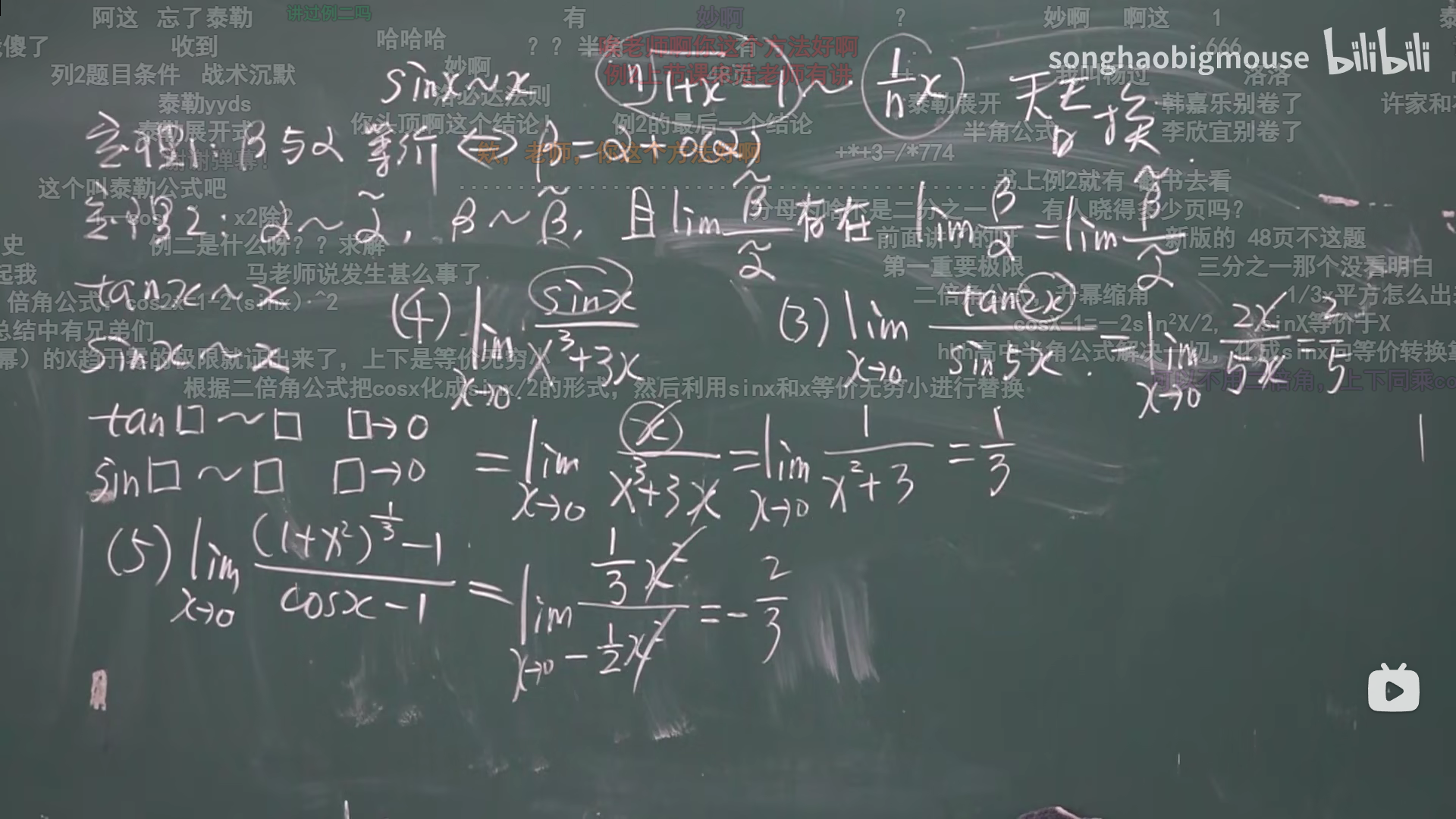
等价无穷小替换的小结论

第八节 函数的连续性与间断性
一。函数的连续性
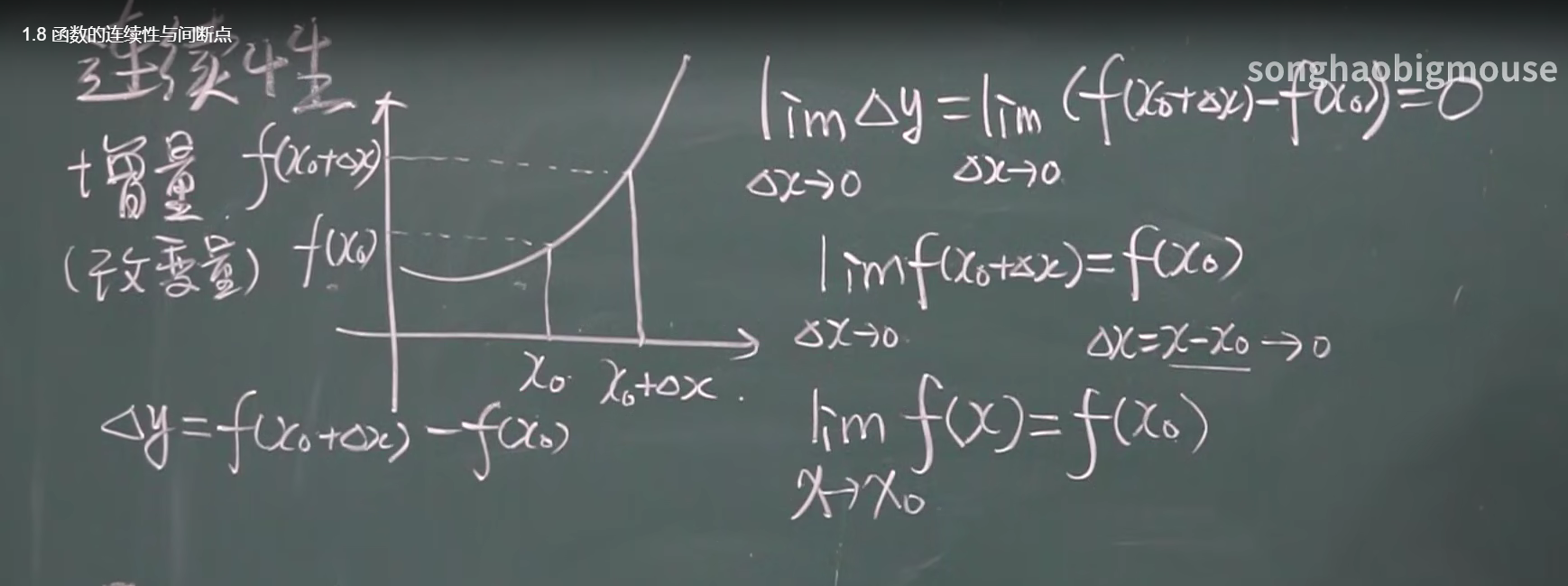
右边两条式子函数连续性的两个定义
连续的要求



三角函数的一些公式 积化和差 和差化积
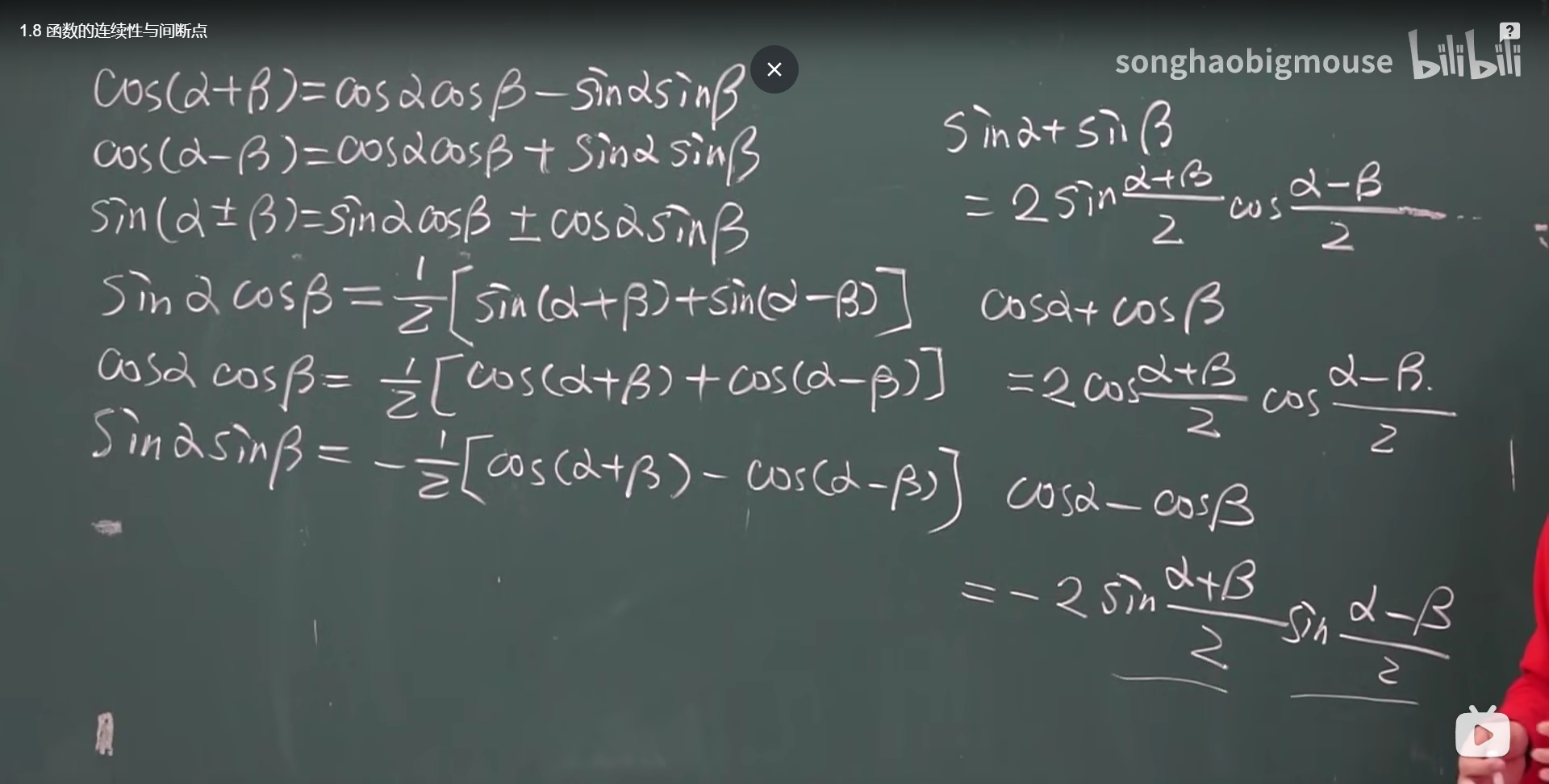
二。函数的间断点
1无穷间断点 2振荡间断点 3可去间断点 4可去间断点 5跳跃间断点

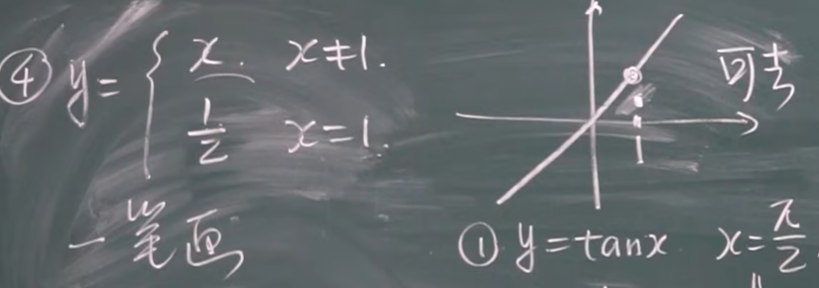
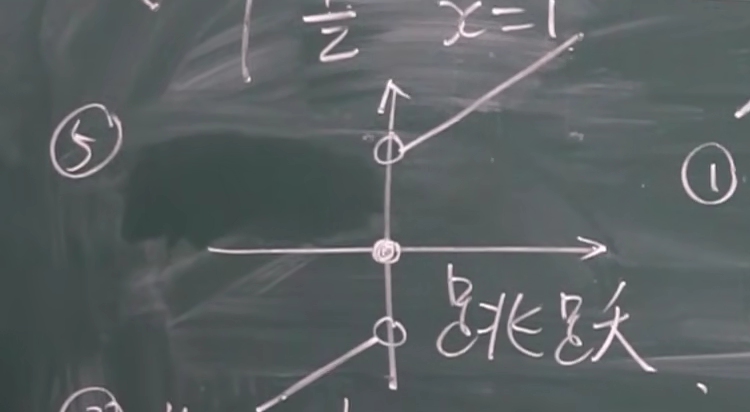
两类间断点的解释

第九节 连续函数的运算与初等函数的连续性
一.连续函数的和差积商的连续性
定理1
设函数f(x)和g(x)在点x0连续,则它们的和(差)f(x)+g(x),f(x)-g(x),积f(x)×g(x),商f(x)/g(x) (g(x)≠0)
二.反函数与复合函数的连续性
定理2
如果函数y=f(x)在区间I上单调增(或单调减少) 且连续 那么他的反函数也在对应区间上单调增加(或单调减少) 且连续
例如 sinx 和 arcSinx cosx 和arcCosx tanx 和 arctinx cotx 和 arccotx
arcSinx arcCosx arctinx arccotx 在他们的定义域都是连续的
定理3
设函数y=f[g(x)]由函数u=g(x)与函数y=f(u)复合而成, 若limg(x)=u0 ,而函数y=f(y)在u=u0连续,那么
$$
lim_{x\rightarrow0}f[g(x)]=f[lim_{x\rightarrow0}g(x)]
$$
定理4
设函数y=f[g(x)] 如果g(x)在x0处连续 g(x0)=u0 而f(u)也在u0处连续 那么复合函数y=f[g(x)]也在x0处连续
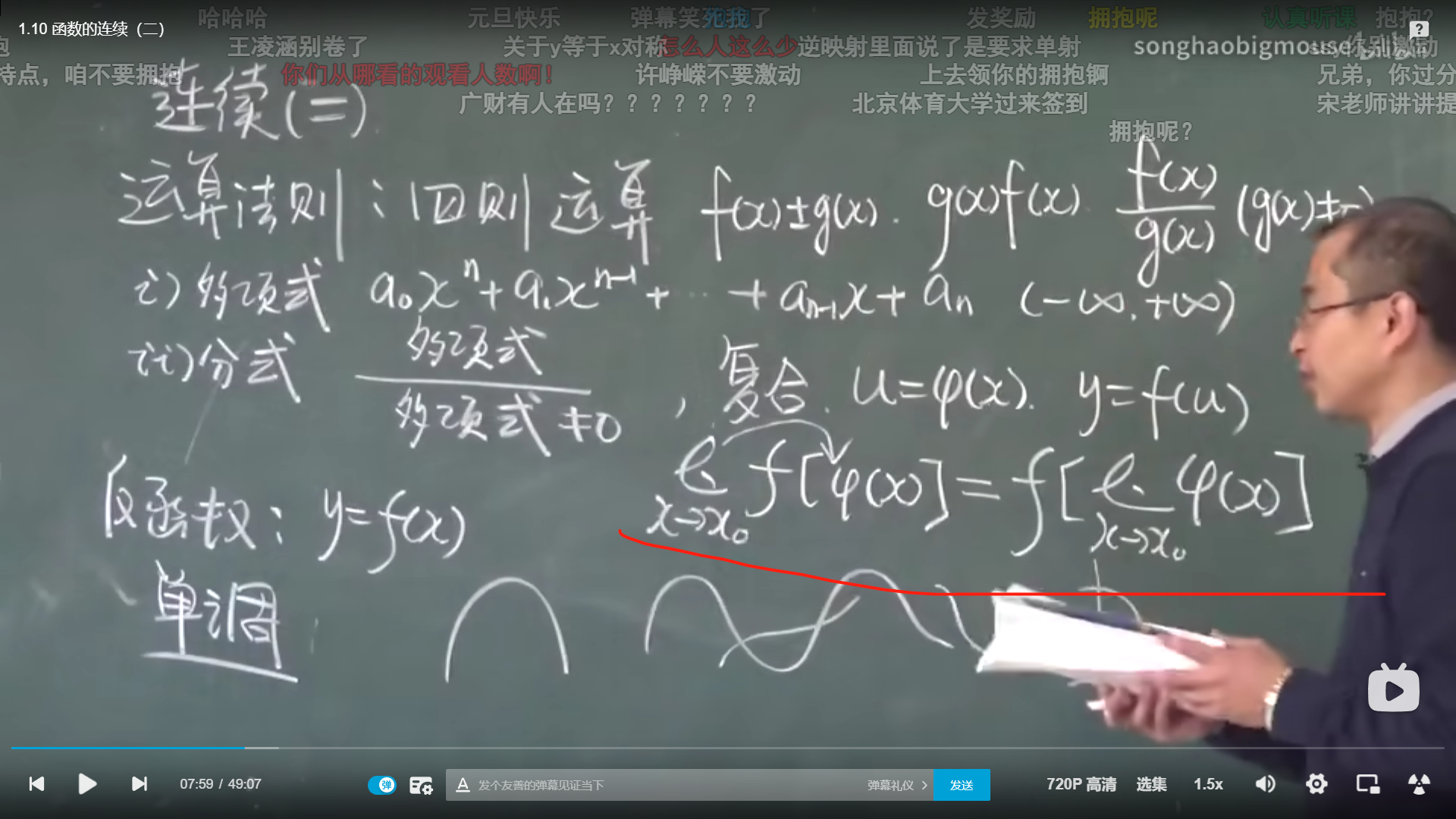
三.初等函数的连续性
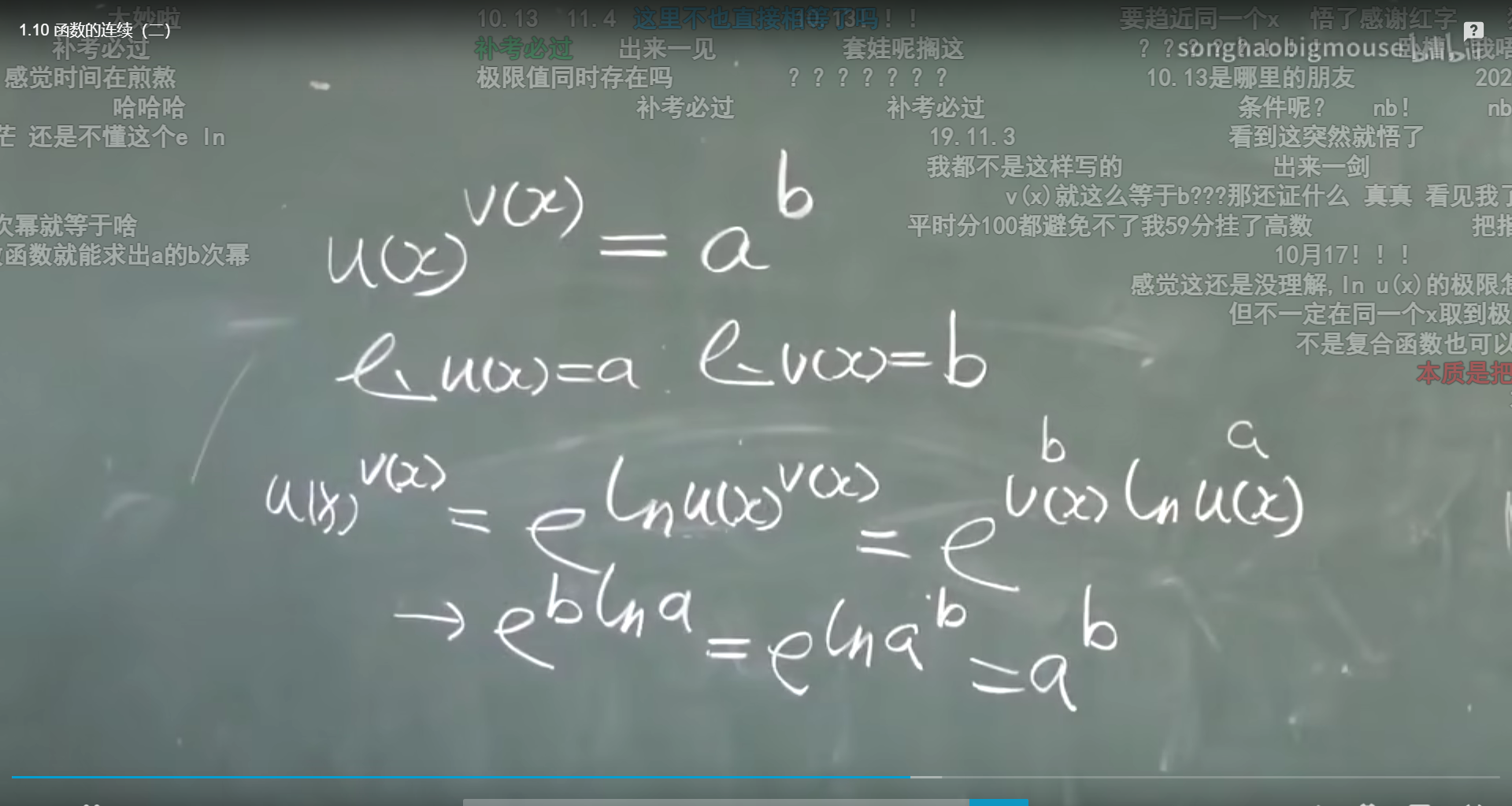
把下面的a和b算出来
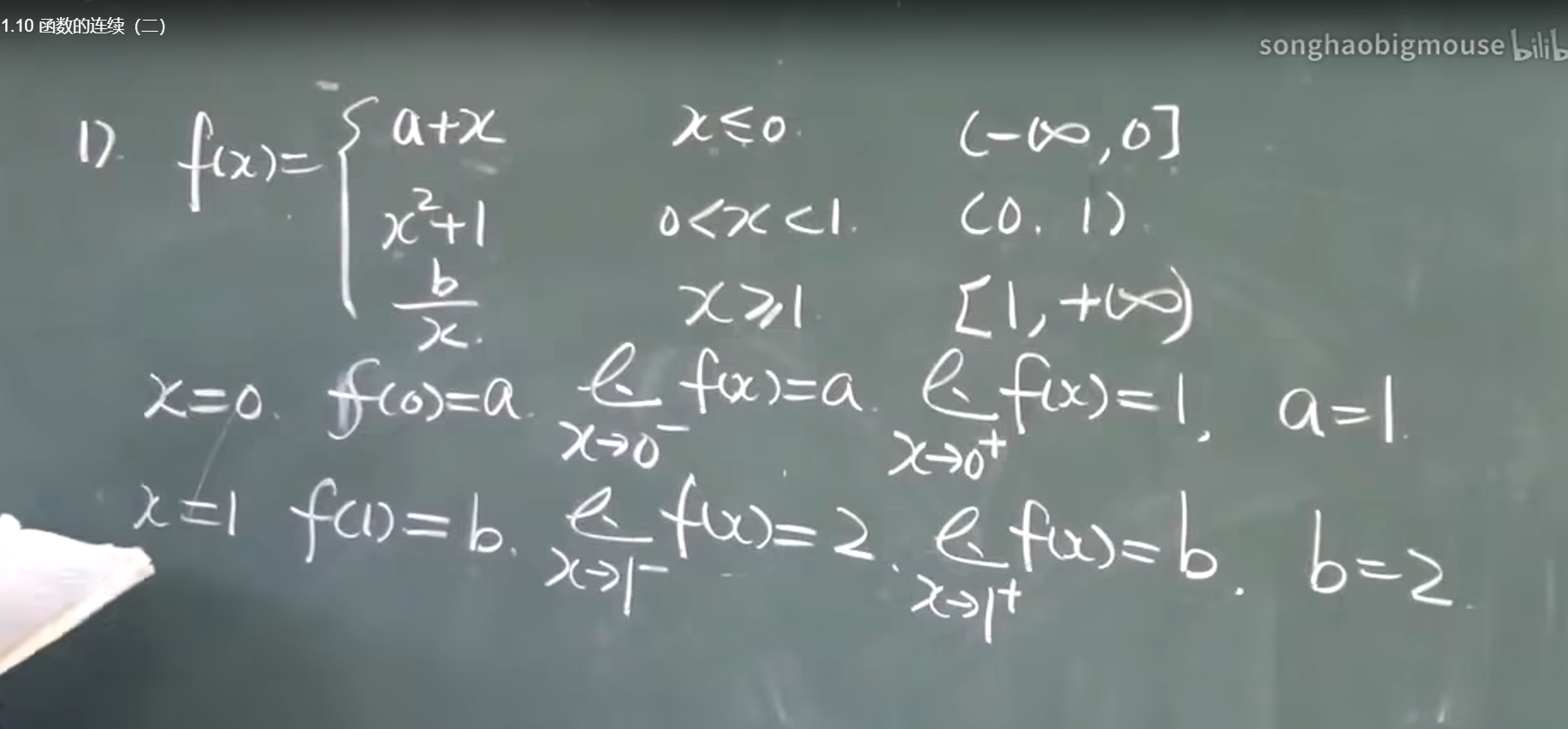
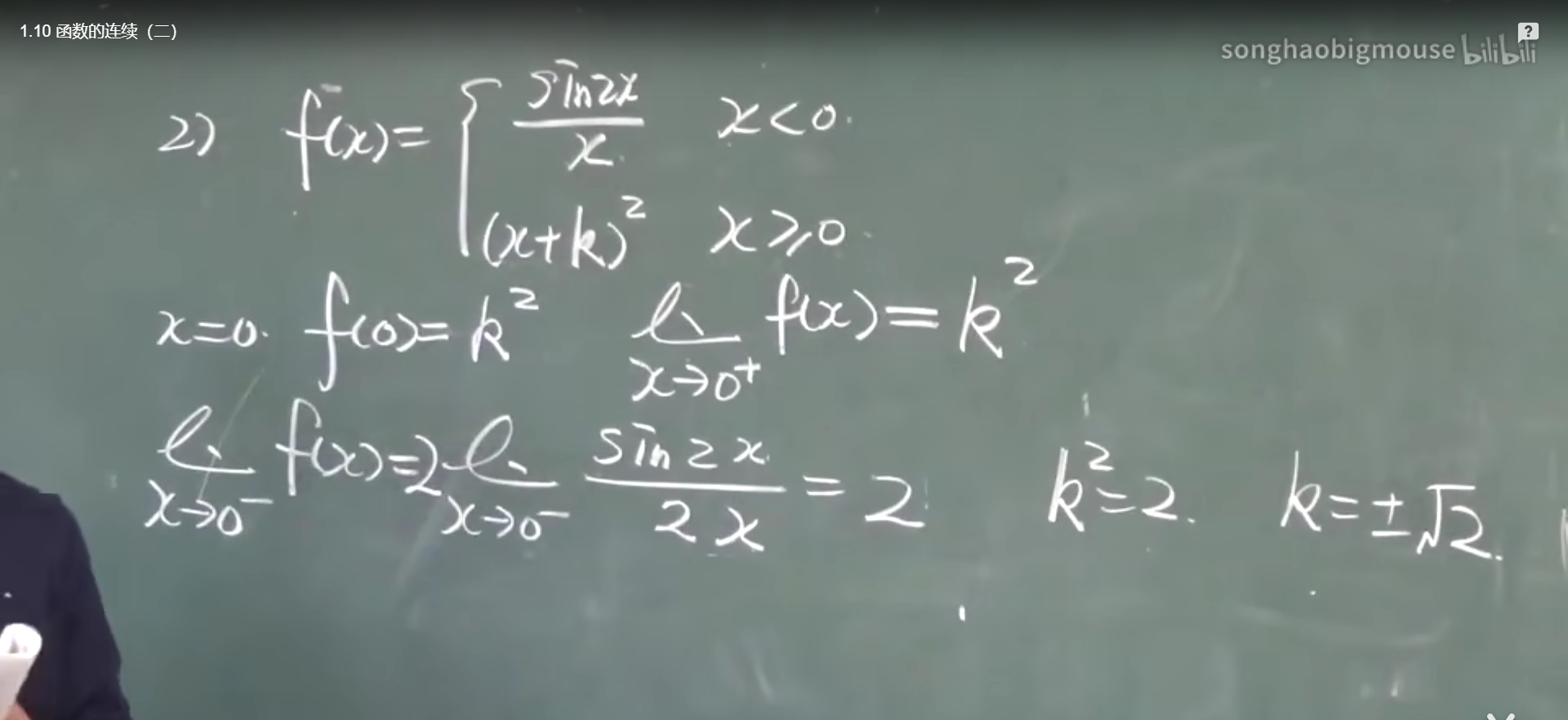
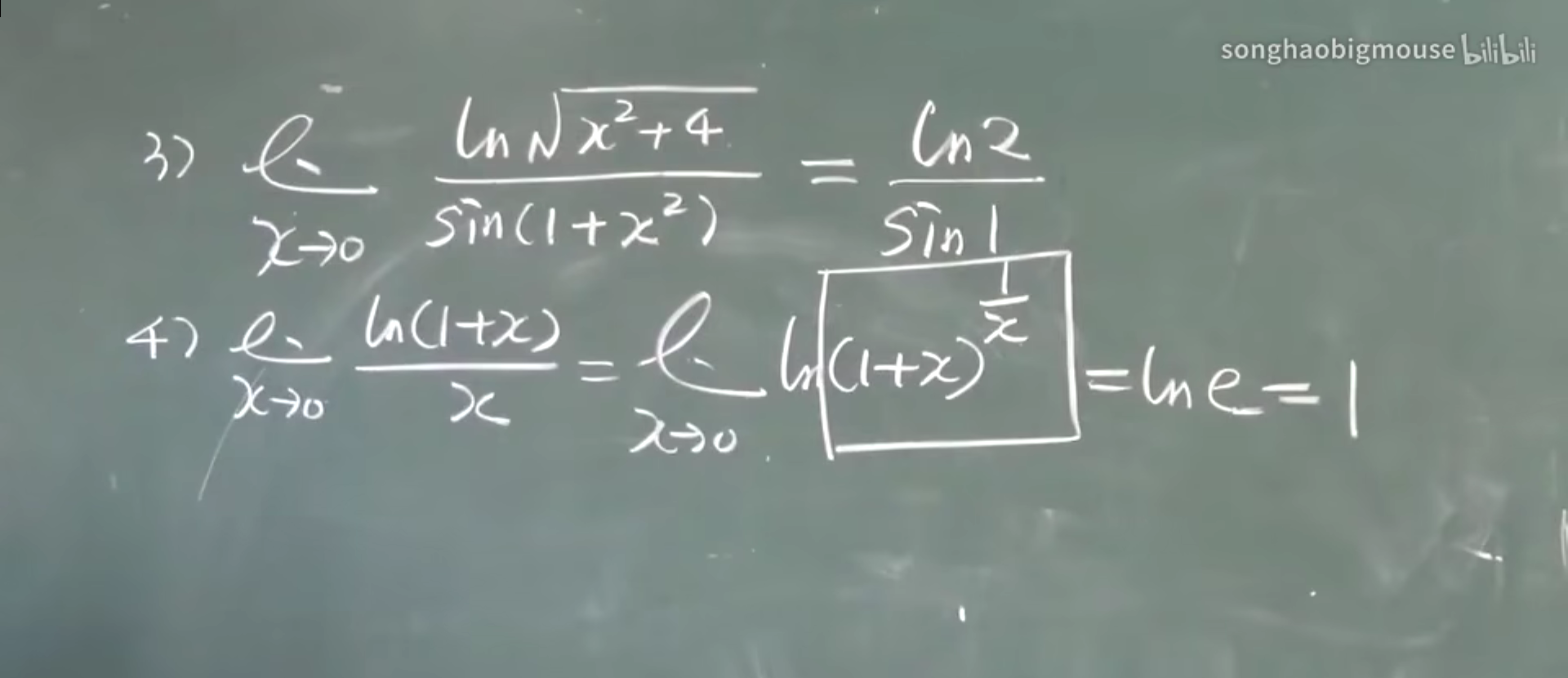
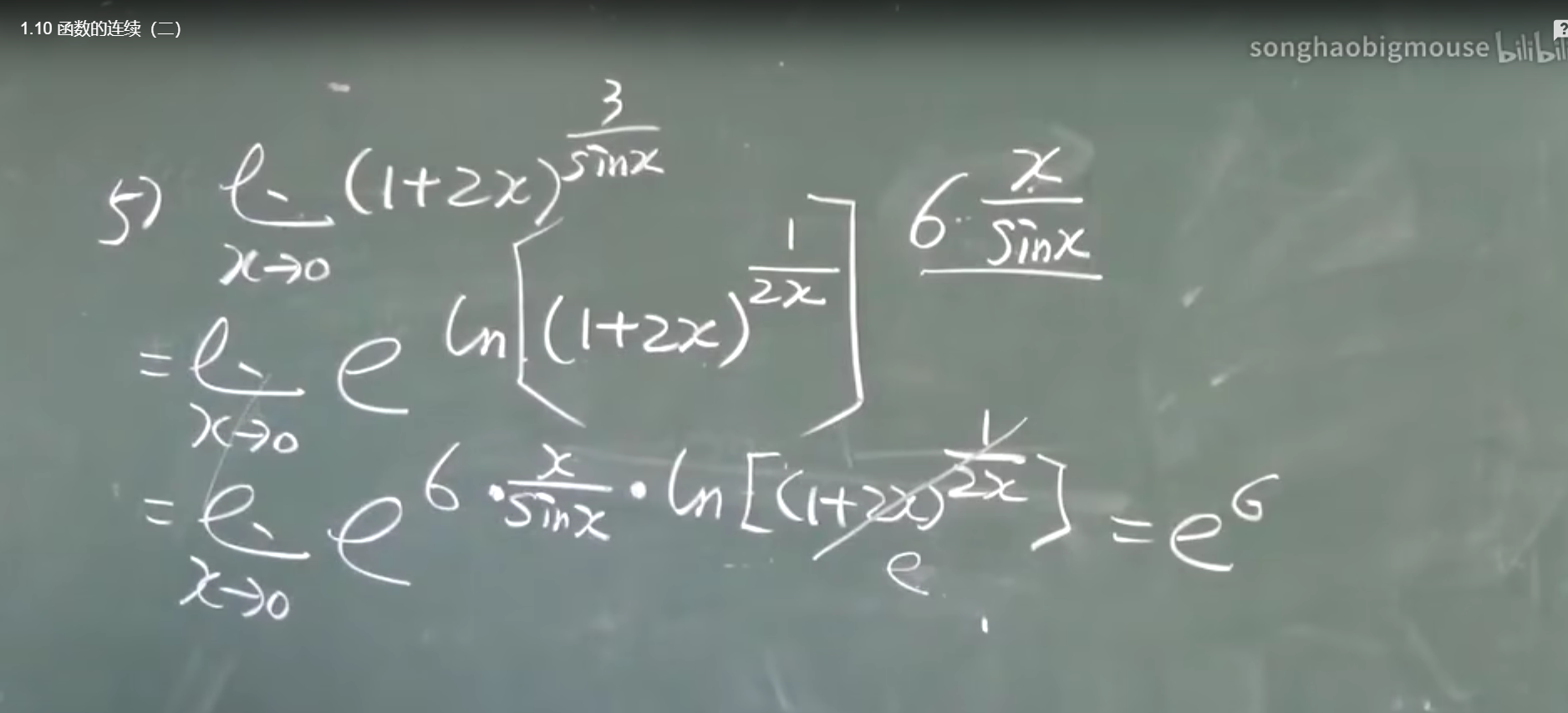
第5题的思路 e抬起法
第十节 闭区间上连续函数的性质
零点定理

介值定理

介值定理的几何理解

题

第二章 导数
1引论

第一节 导数的定义

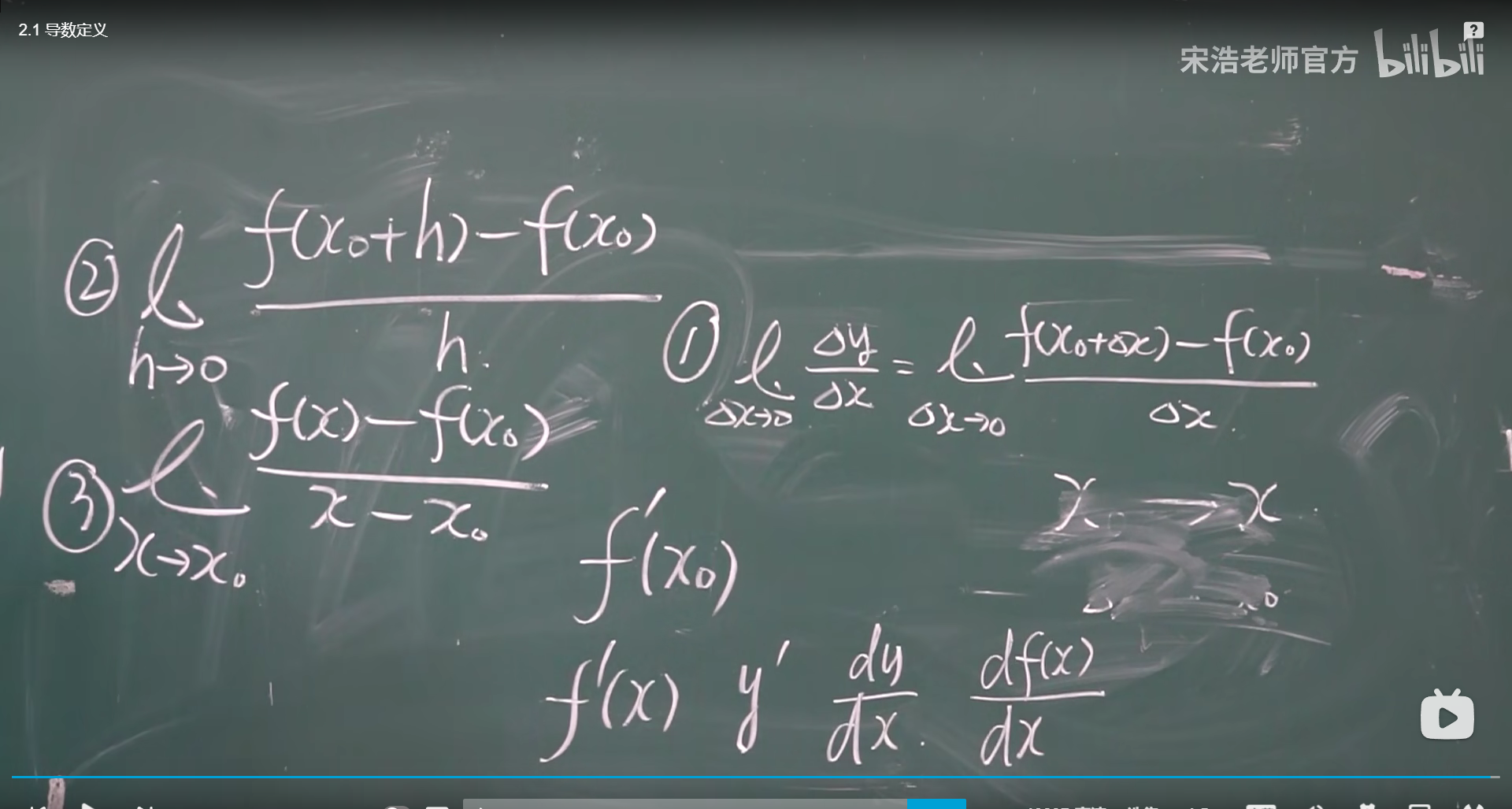
常用求导公式举例
就是那个求导怎么来见书本p77 或库课p56
单侧导数
f(x)在x0可导的充分必要条件是左导数右导数存在且相等
三。导数的几何意义
通过斜率求切线方程
记住斜截式

四。函数可导性与连续性的关系
x0处可导则连续
连续不一定可导
第二节 求导法则

反函数求导法则
卧槽宋
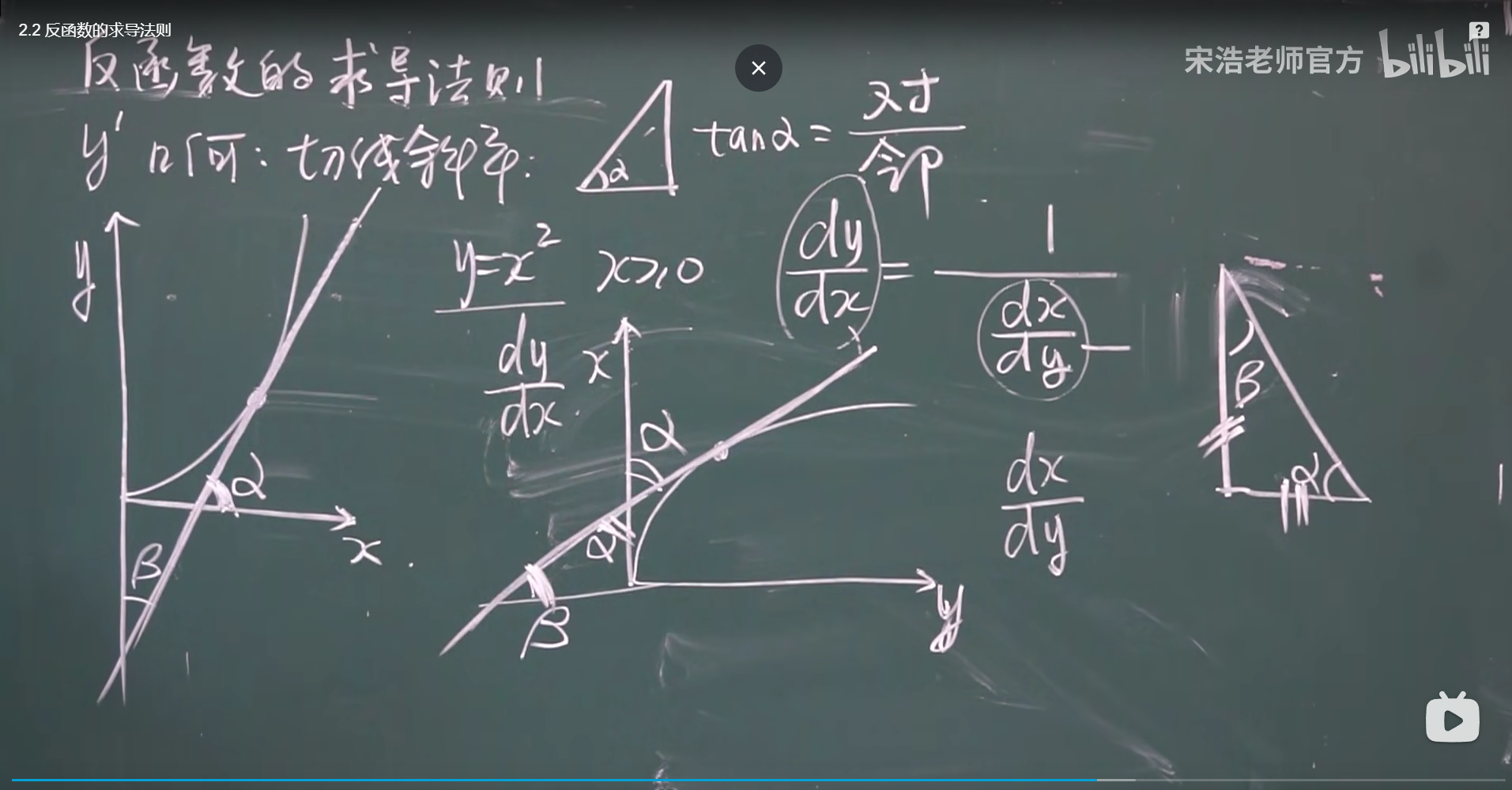
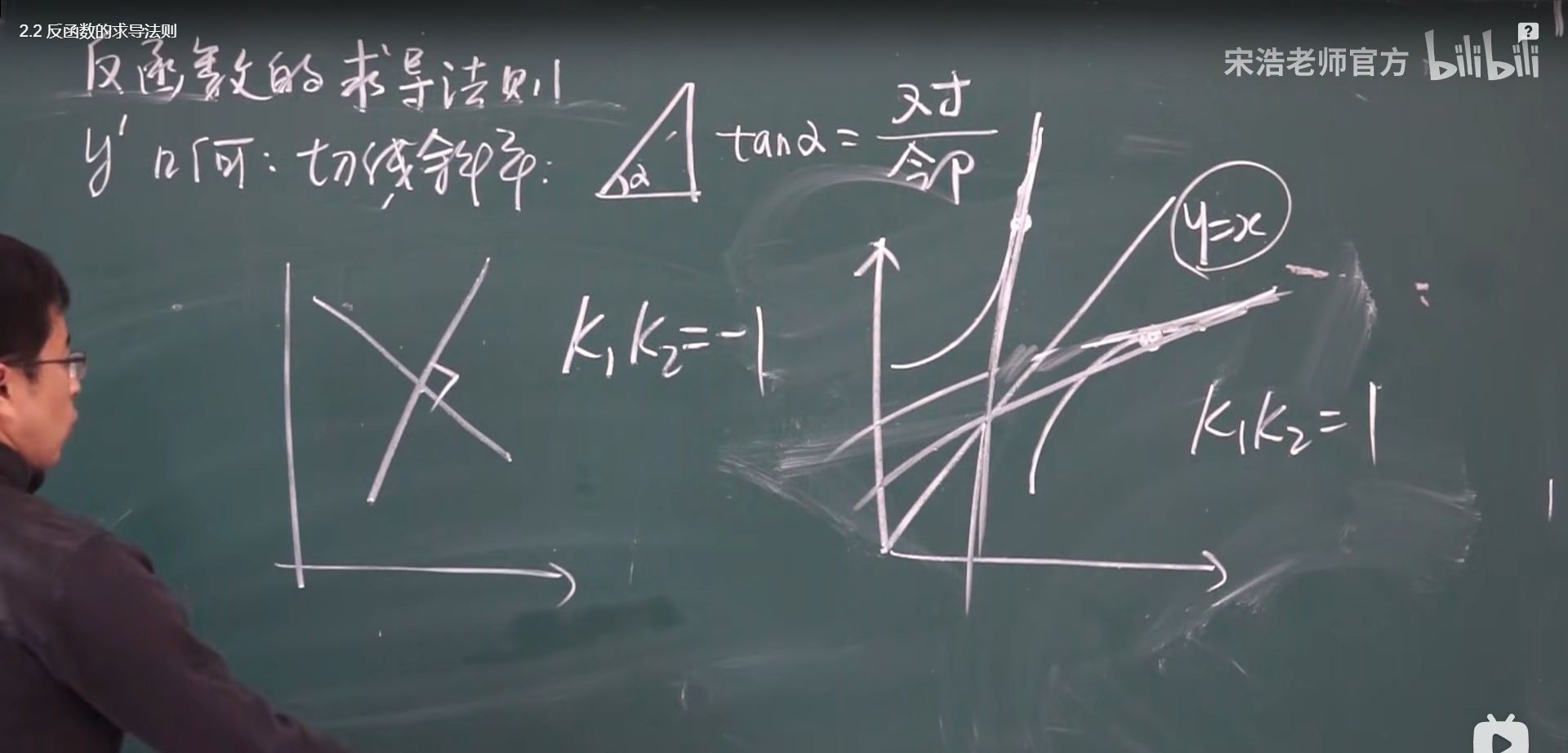
k1×k2 = 1 成对称
复合函数求导 怪题
x^x的时候 对数求导
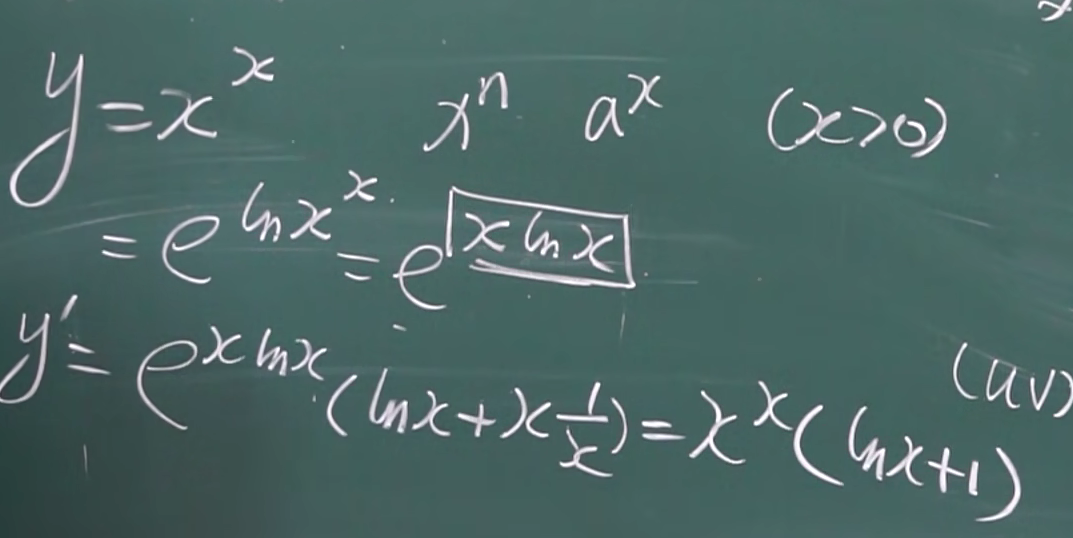
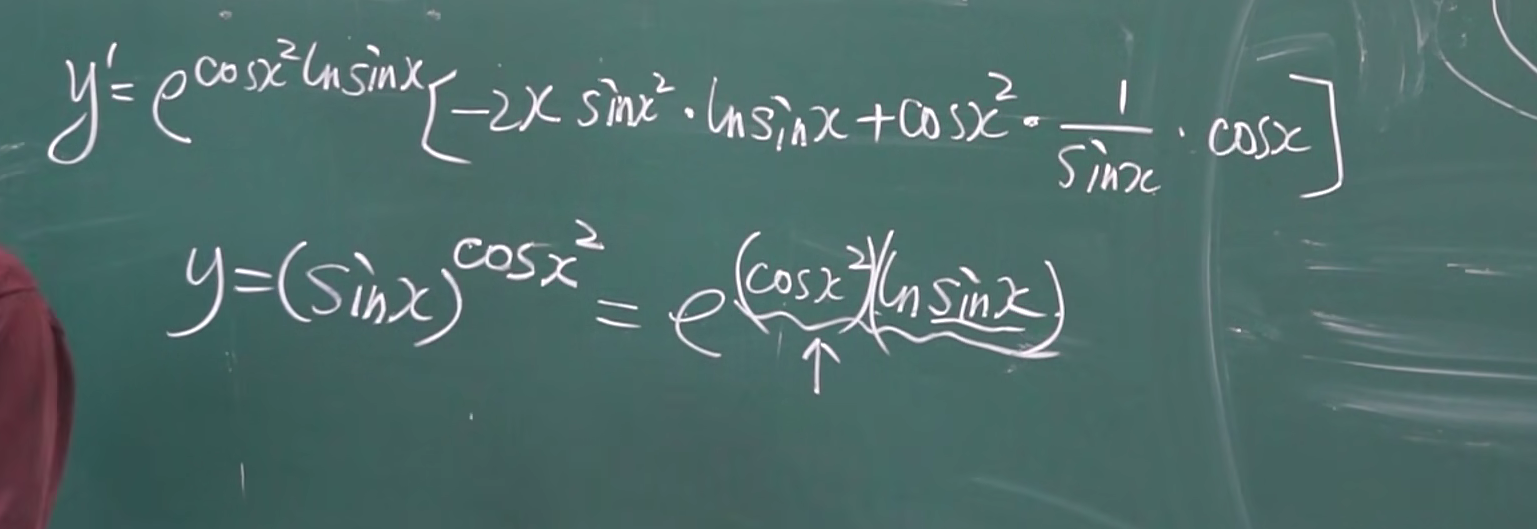
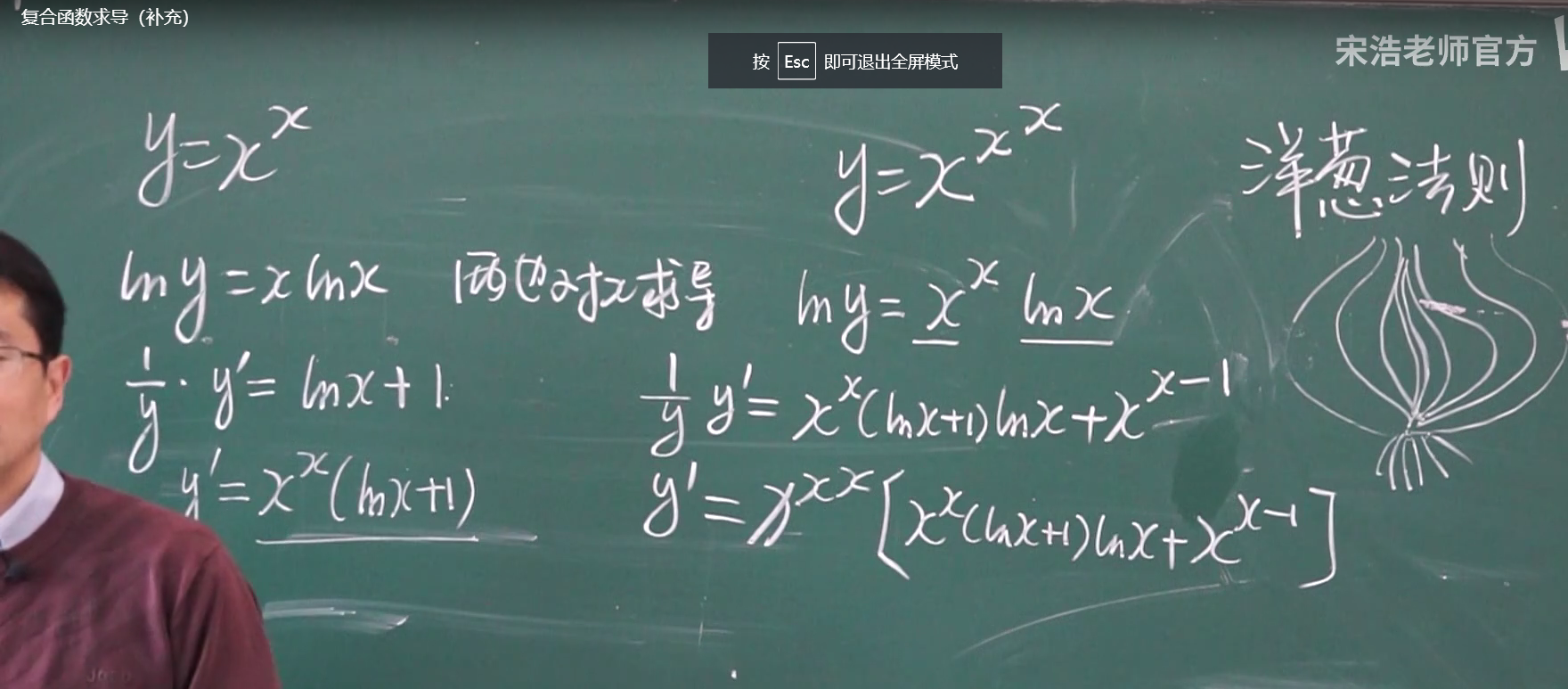
题
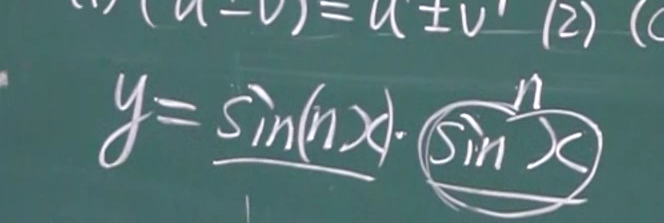
上下联合
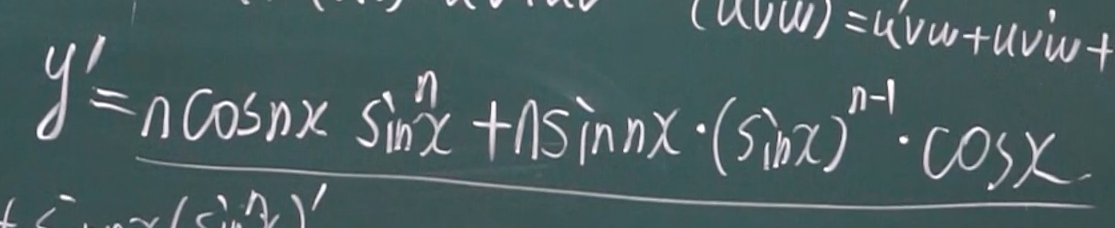
第三节 高阶导数
多次求导
书本和笔记上的n阶导数公式
第四节 隐函数 对数导数 参数求导
隐函数

对数求导(5)

对数求导

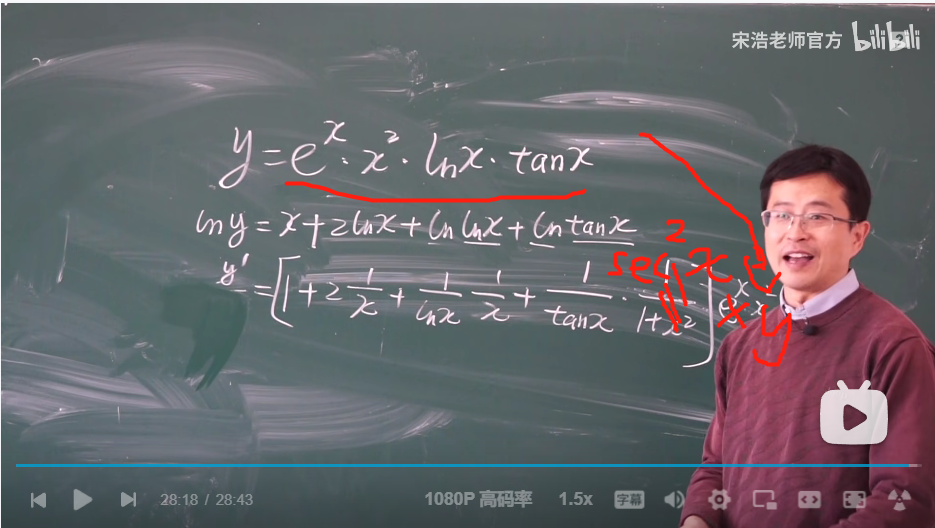
参数方程求导

参数方程二阶导

参数高阶求导

第五节 函数的微分
微分就是求导后加dx
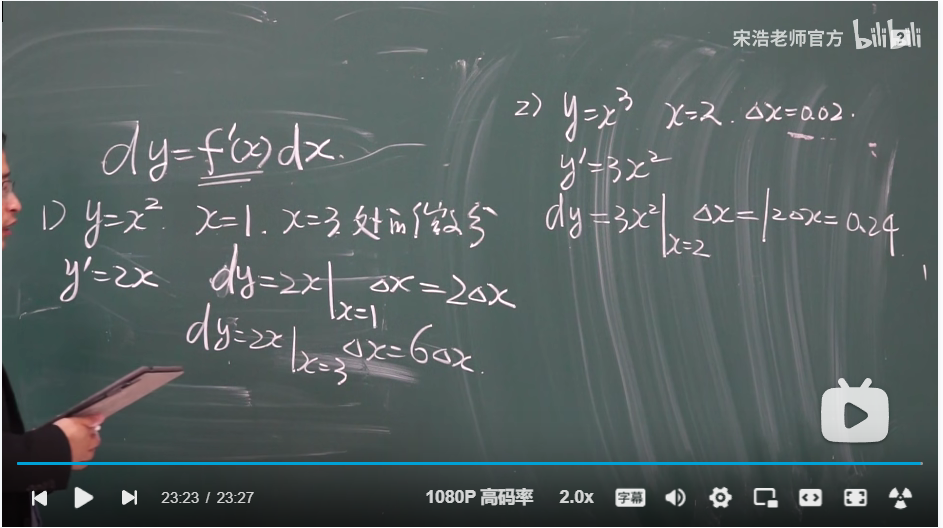
复合微分也是直接导 加dx

微分的几何意义
函数的近似计算

▲x趋于零 才会比较准确 所以下面的那个是不怎么可取的▲太大了 误差会更大
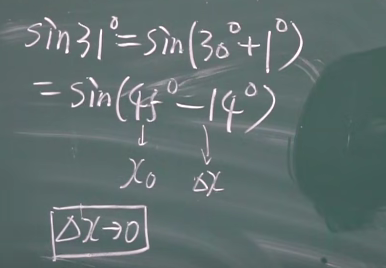
另外的一个角度理解题

近似计算的公式

第三章 微分中值定理及其导数的应用
罗尔中值定理
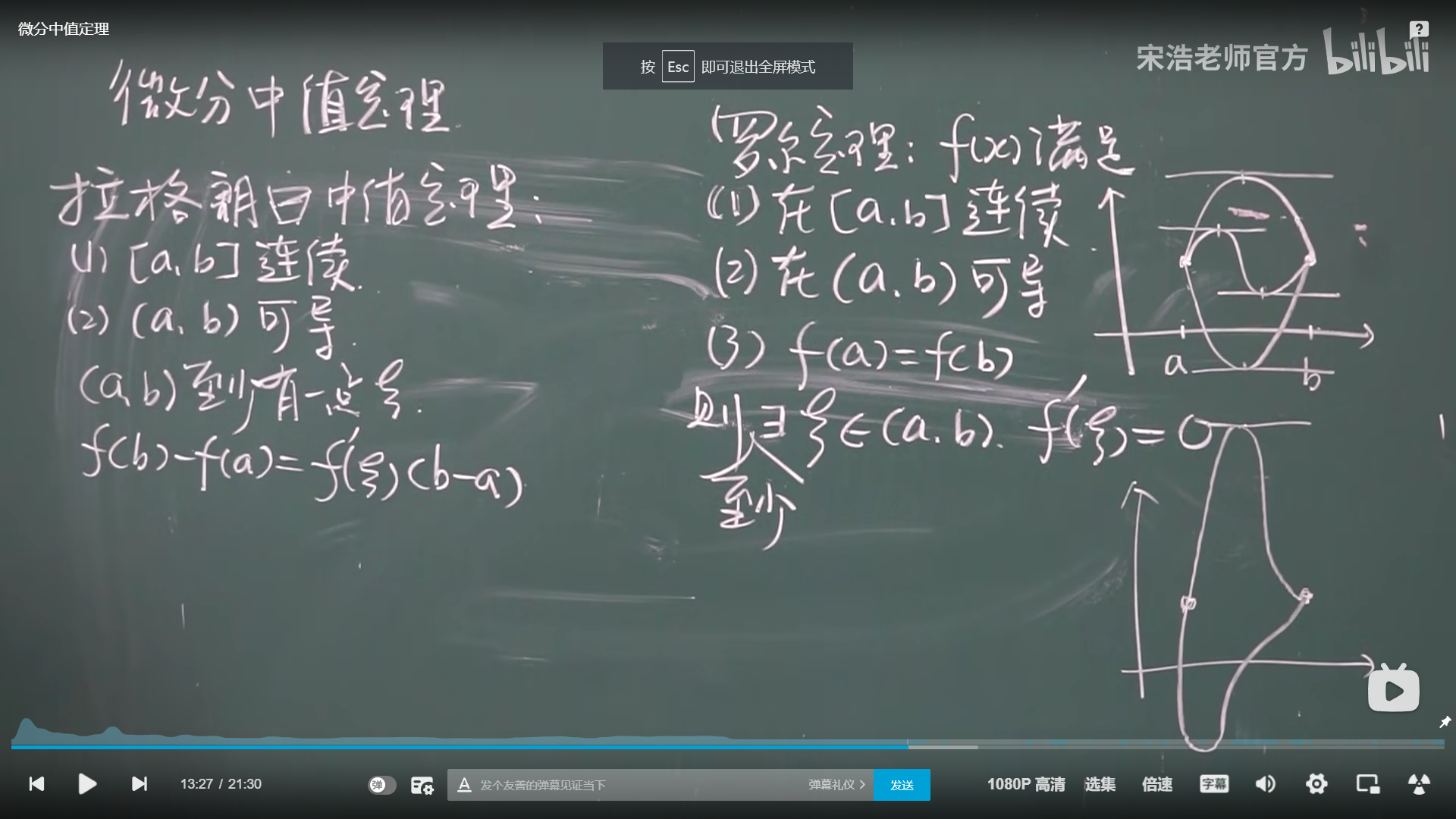
拉格朗日中值定理

推论1

柯西中值定理

柯西→拉格朗日→罗尔
洛必达
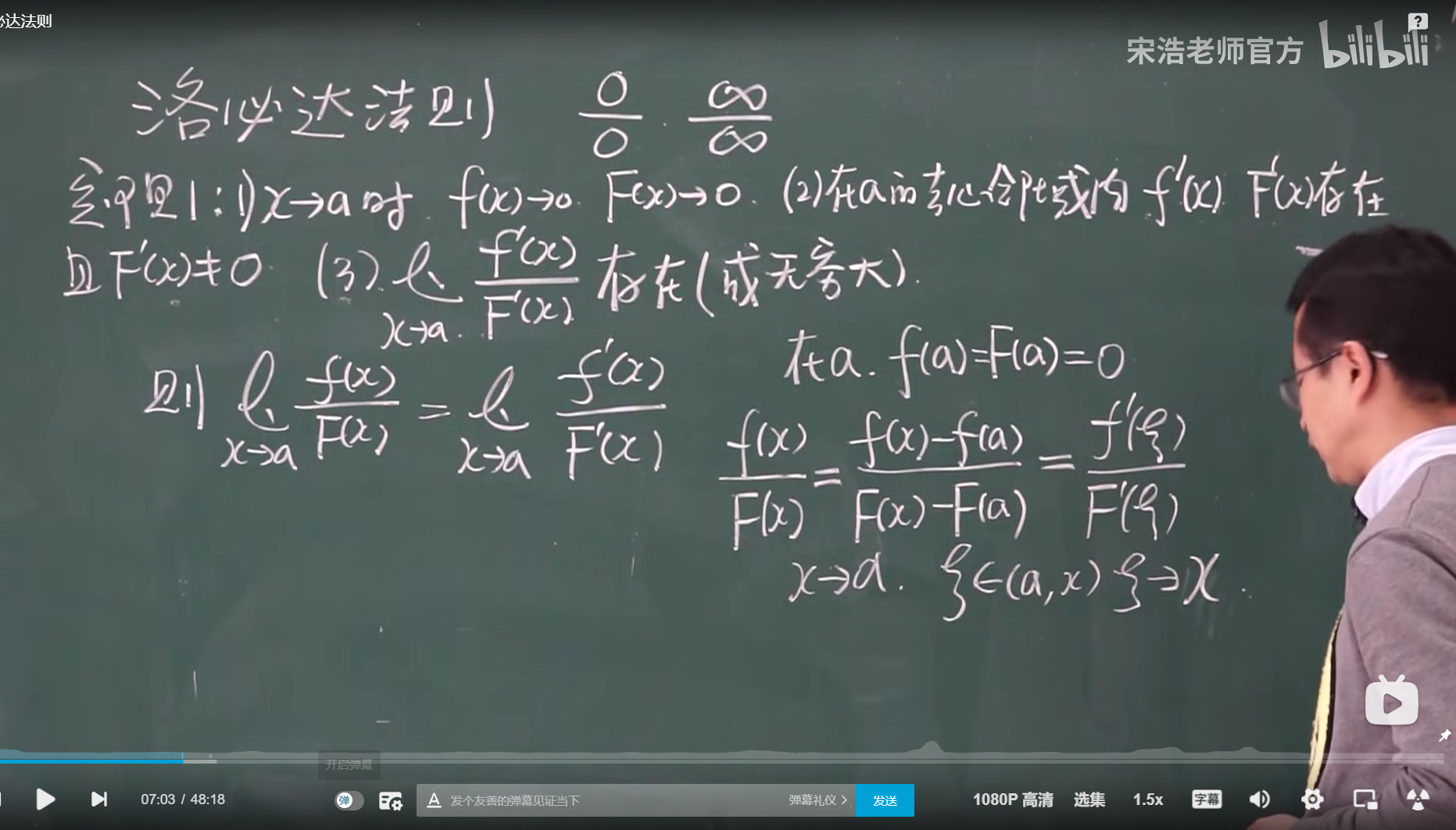
洛必达三种情况

洛必达例题题目
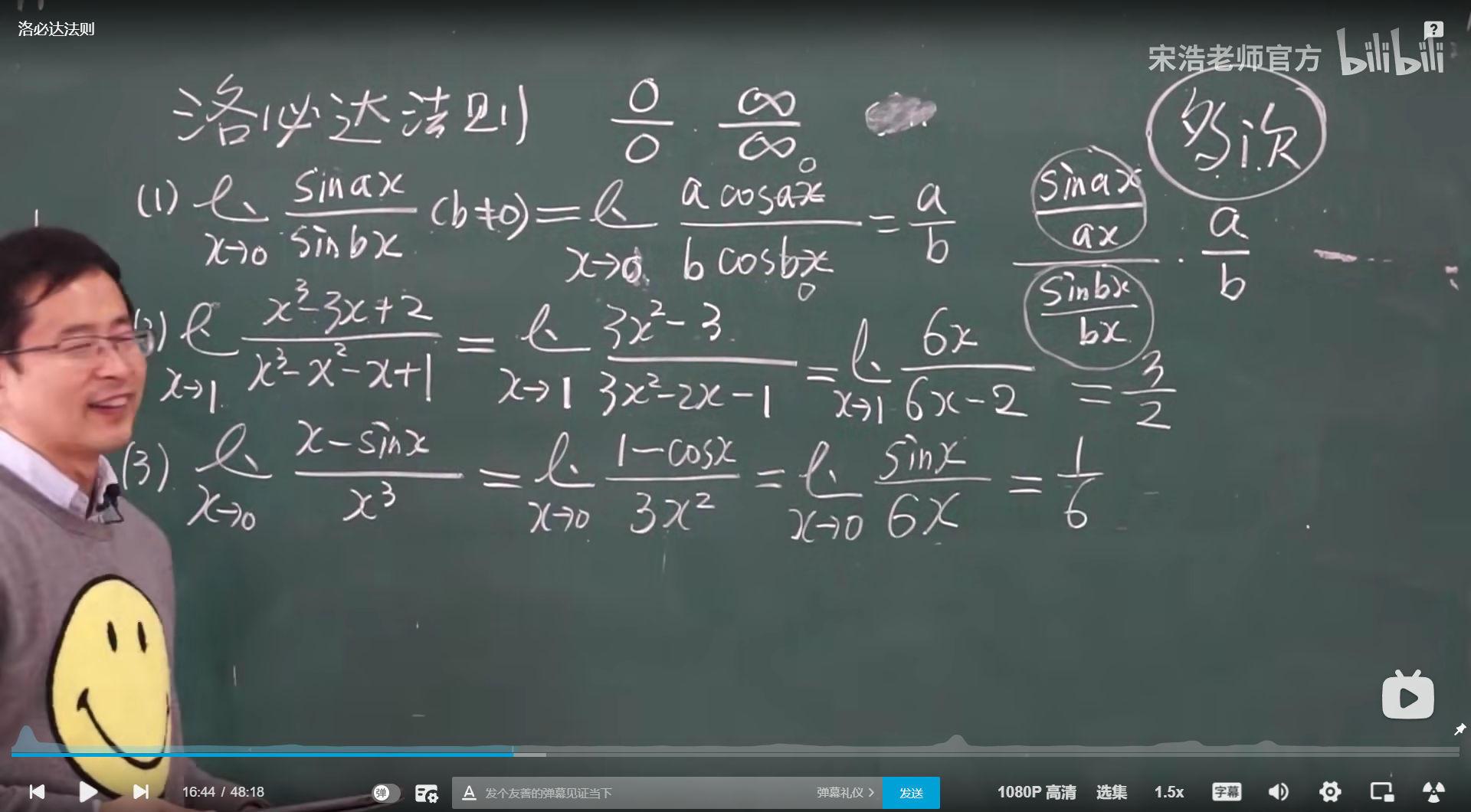

例题6的变种
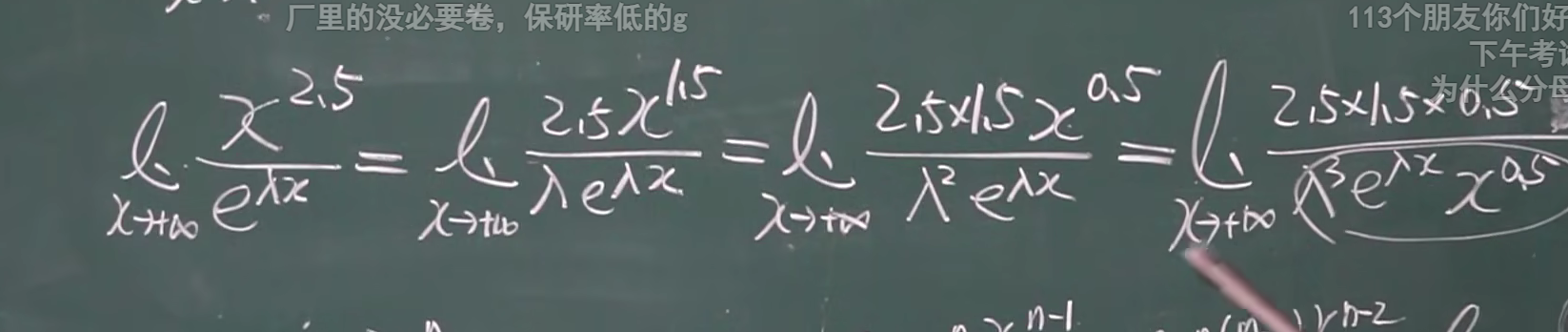

第10题和小技巧

5。尽量把常数朝外面摞


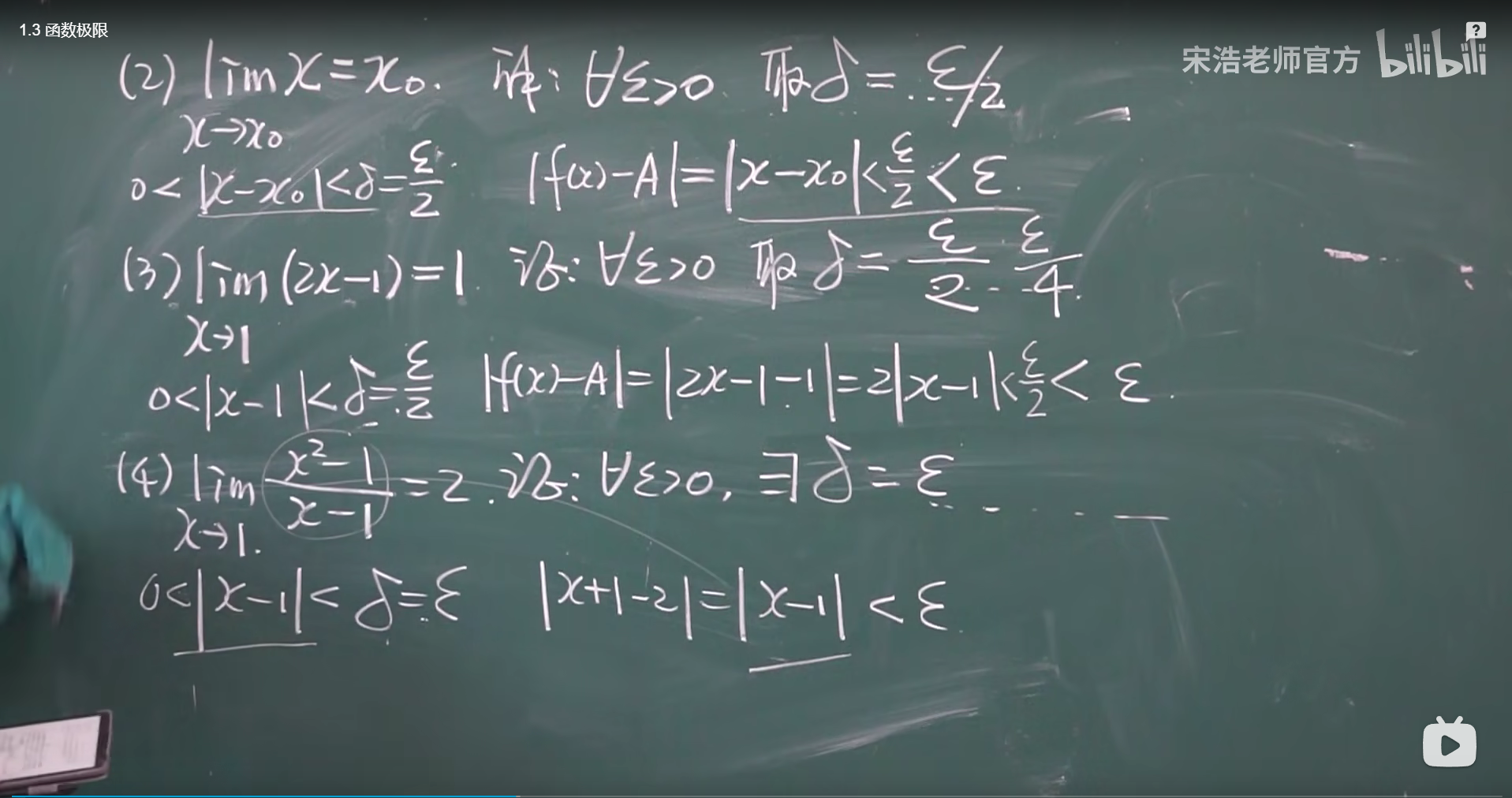


 浙公网安备 33010602011771号
浙公网安备 33010602011771号