1. 全连接神经网络

事实上深度学习和人脑学习的思维差不多，学习的时候不断做题，做错了题就根据答案巩固知识点，更新脑子里的知识

深度学习也是，重复{前向传播、计算损失函数、反向传播}这样一个过程，完善自己的模型

1. 模型

如果全连接的计算的函数是\(f(x)\)，激活函数是\(h(x)\)，实际上4层的全连接神经网络最后输出的就是\(h(f(f(f(f(x)))))\)

和初中数学kx+b不一样的是，k、x、b都是矩阵

2. 激活函数

2.1 sigmoid

\[\mathrm{y=\frac{1}{1+e^{-z}}\Longrightarrow y^{\prime}=y(1-y)} \]

Sigmoid函数优点：
1、简单、非常适用分类任务;

Sigmoid函数缺点：
1、反向传播训练时有梯度消失的问题
2、输出值区间为(0,1)，关于0不对称;
3、梯度更新在不同方向走得太远，使得优化难度增大，训练耗时

2.2 Tanh

\[\mathrm{y=\frac{e^z-e^{-z}}{e^z+e^{-z}}\Rightarrow y^{\prime}=1-y^2} \]

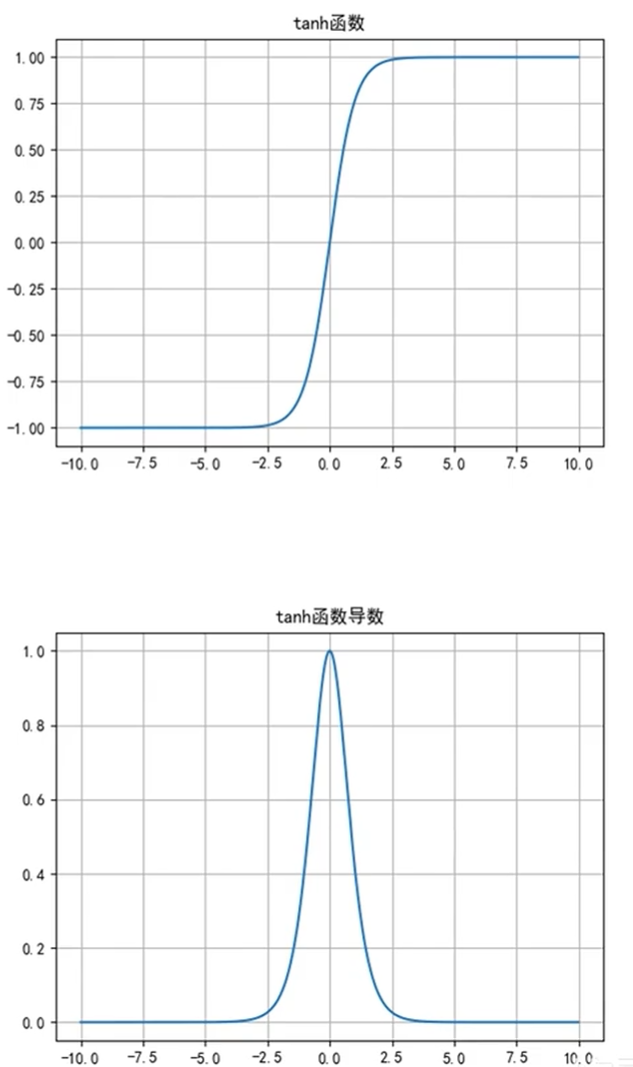
函数本体的值域和导数的值域都比sigmoid更大

Tanh函数优点：
1、角解决了Sigmoid函数输出值非0对称的问题
2、训练比Sigmoid函数快，更容易收敛;
Tanh函数缺点：
1、反向传播训练时有梯度消失的问题
2、Tanh函数和Sigmoid函数非常相似。

2.3 ReLU

\[y= \begin{cases} z & \mathrm{~if~}z>0 \\ 0 & \mathrm{~if~}z<=0 & \end{cases}\Longrightarrow y^{\prime}= \begin{cases} 1 & \mathrm{~if~}z>0 \\ 0 & \mathrm{~if~}z<=0 & & \end{cases}\]

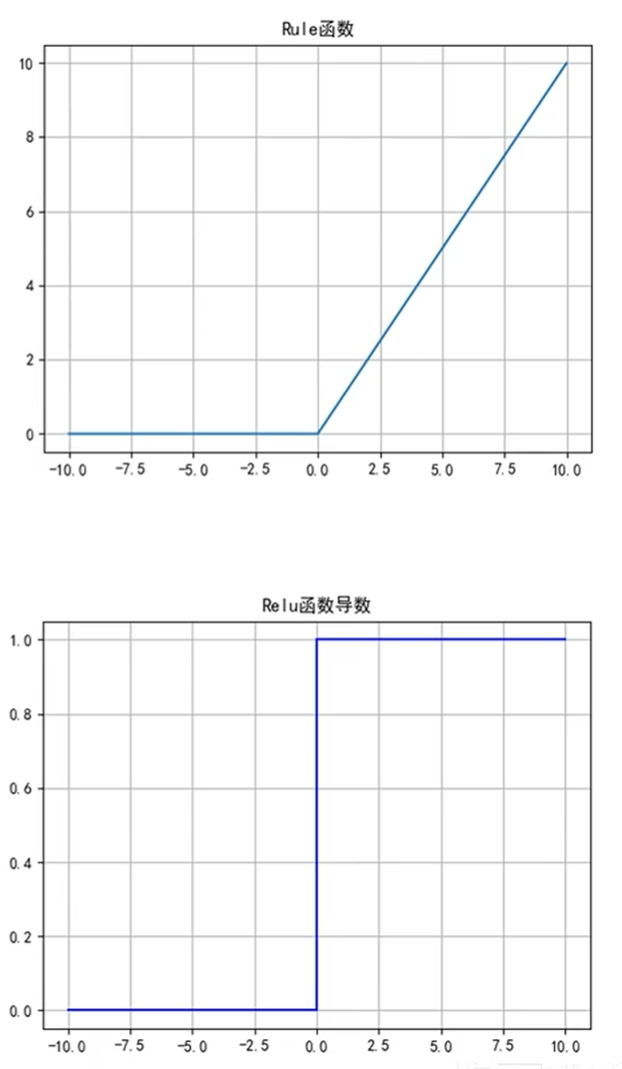
ReLU函数优点：
1、解决了梯度消失的问题
2、计算更为简单，没有Sigmoid函数和Tanh函数
的指数运算;
ReLU函数缺点：
1、训练时可能出现神经元死亡;

2.4 leaky ReLU

\[\mathrm{y}= \begin{cases} \mathrm{z} & \mathrm{~if~z>0} \\ \mathrm{az} & \mathrm{~if~z<=0} & \end{cases}\Longrightarrow\mathrm{y}^{\prime}= \begin{cases} 1 & \mathrm{~if~z>0} \\ \mathrm{~a} & \mathrm{~if~z<=0} & & \end{cases}\]

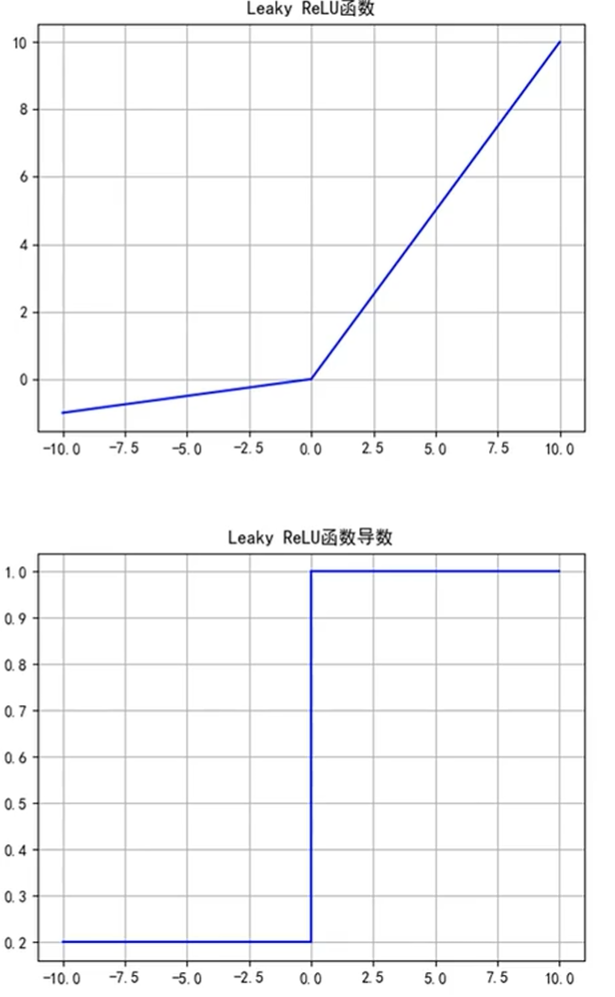
Leaky ReLU函数优点：
1、解决了ReLU的神经元死亡问题；
Leaky ReLU函数缺点：
1、无法为正负输入值提供一致的关系预测(不同区间函数不同)

3. 前向传播计算过程

按照上图，有计算过程：

\[\begin{gathered} a_{11}=\mathrm{sigmoid}(x_{1}w_{11}+x_{2}w_{13}+b_{1}) \\ a_{12}=\mathrm{sigmoid}(x_{1}w_{12}+x_{2}w_{14}+b_{2}) \\ a_{21}=\mathrm{relu}(a_{11}w_{21}+a_{12}w_{22}+b_{3}) \\ y=a_{21} \end{gathered}\]

4. 损失函数

均方误差的损失函数：\(J(x)=\frac{1}{2m}\sum_{i=1}^m(f(x_i)-y_i)^2\)

事实上深度学习和人脑学习的思维差不多，学习的时候不断做题，做错了题就根据答案巩固知识点，更新脑子里的知识

深度学习也是，重复{前向传播、计算损失函数、反向传播}这样一个过程，完善自己的模型

5. 梯度下降

https://www.cnblogs.com/ratillase/p/17745372.html

\[\begin{cases} w=w-a\frac{d}{dw}J(w,b) \\ b=b-{\alpha}\frac{d}{db}J(w,b) & \end{cases}\]

6. 前向传播计算过程

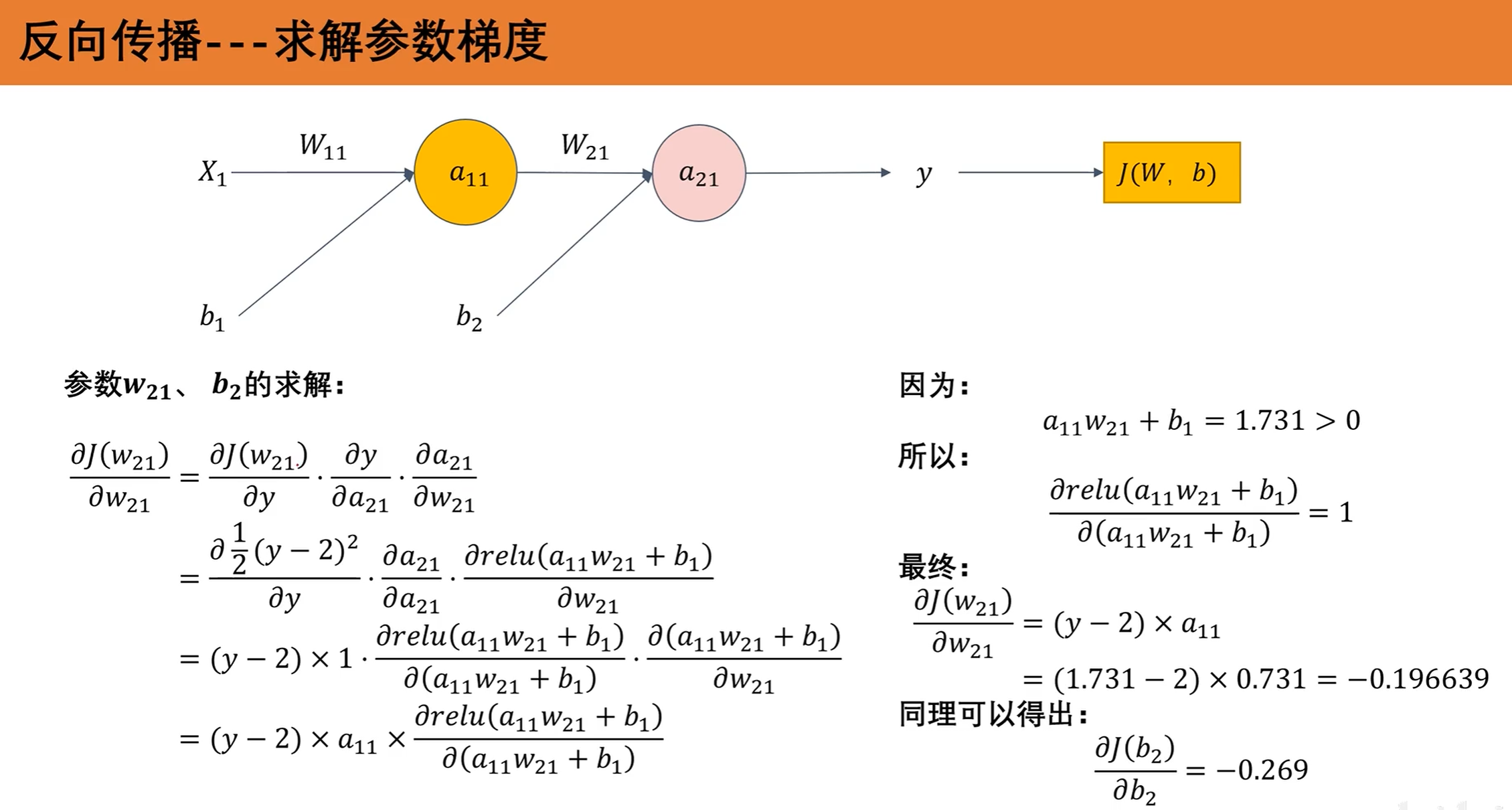
7. 整体过程

1. 准备数据，例10000个(x,y)
2. 建立模型model
3. 设置参数，开始训练-> 学习率、训练batch等等

• 3.1 前向传播
• 3.2 计算损失
• 3.3 反向传播，梯度下降
• 3.4 更新参数
• 3.5 重复直到训练批次结束

4. 进行测试
5. 应用

8. 全连接神经网络存在的问题

参数冗杂
全连接层对于空间信息的损失较多，空间结构的表达性不足