监督学习
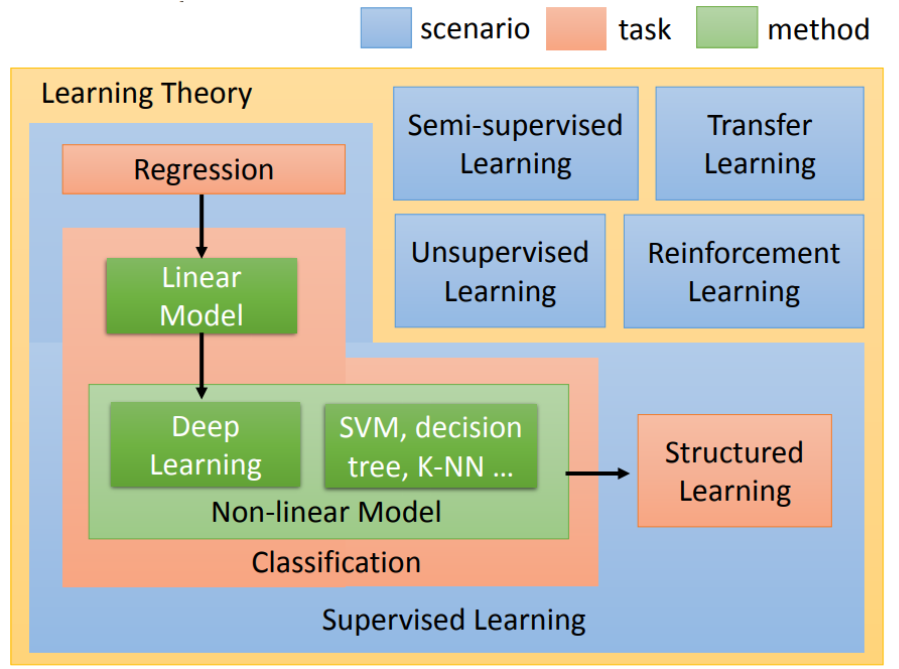
1. 监督学习和无监督学习
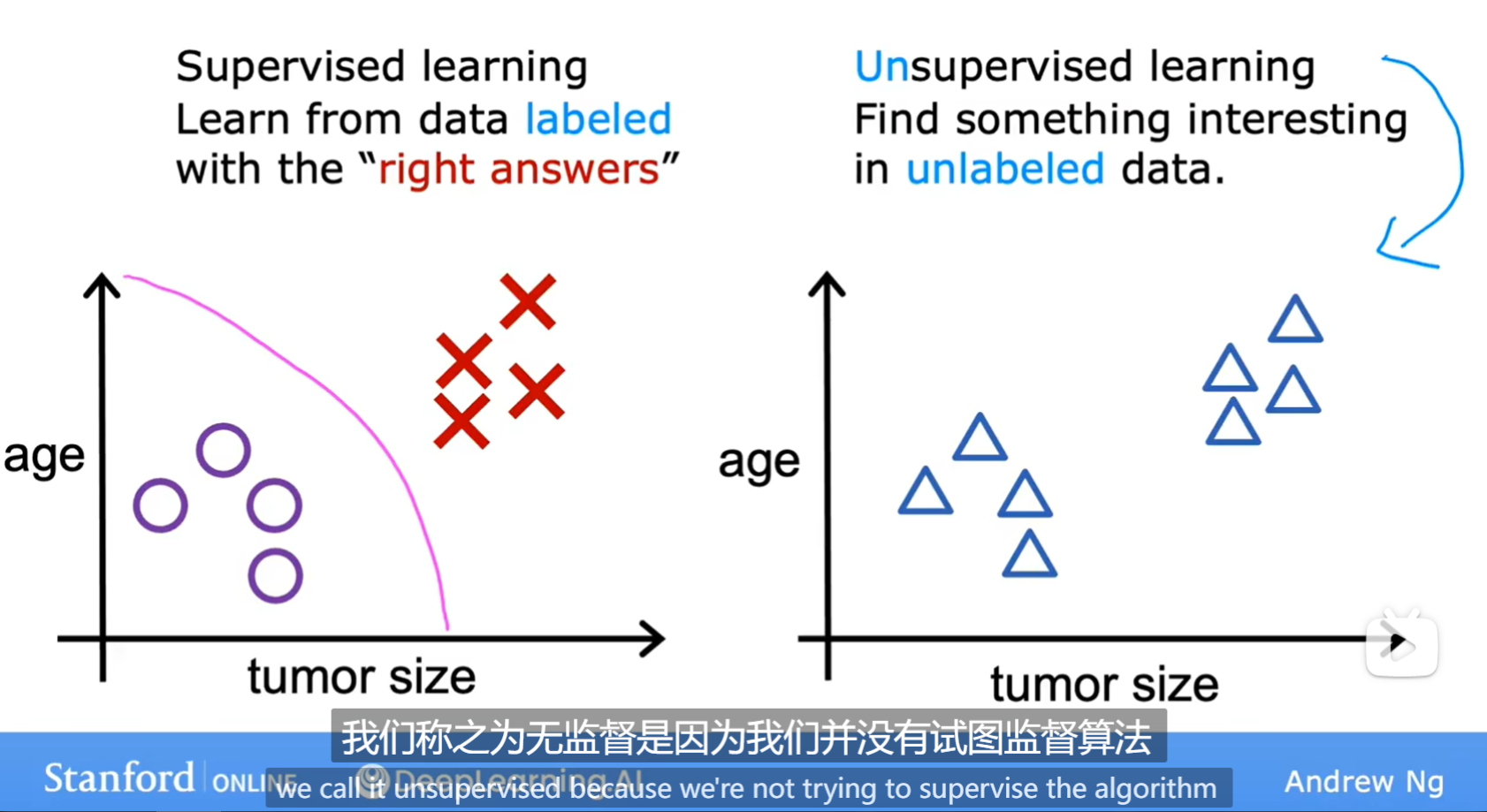
- 监督学习有规定的输入输出,无监督学习没有
监督学习的两种主要类型:回归和分类
举例无监督学习:
- 聚类(clustering algorithm):例如将搜索界面将相关的新闻关联在一起、找到DNA有共性的分组、分析主要用户需求
- 异常检测(anomaly detection):检测异常
- 降维(dimensionality reduction):将大数据组降成小数据组,同时丢失尽量少的信息
2. 线性回归(linear regression)
\[y = wx + b
\]
使用\((x^{(i)} , y^{(i)})\)表示数据中第i对值
Numpy数组有一个 .shape 参数。x_train.shape 返回一个 python 元组,每个维度都有一个条目。x_train.shape[0] 是数组的长度和示例数
import numpy as np
import matplotlib.pyplot as plt
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train.shape: {x_train.shape}")
m = x_train.shape[0]
print(f"Number of training examples is: {m}")
输出结果为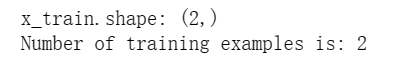
也可以使用len,即m = len(x_train),输出结果仍为2
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()
绘制如图: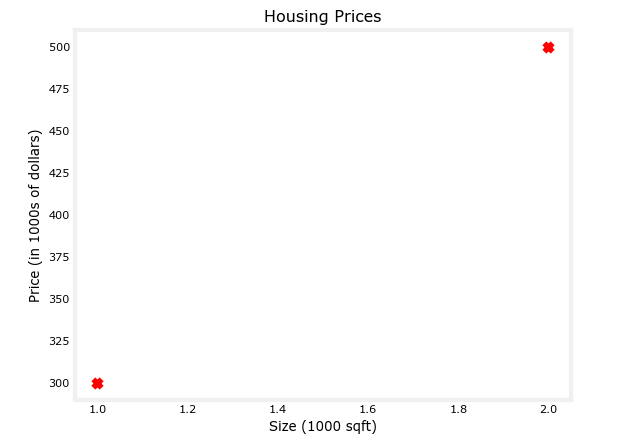
3. 代价函数
代价函数是评价回归模型的一个指标,有助于优化模型

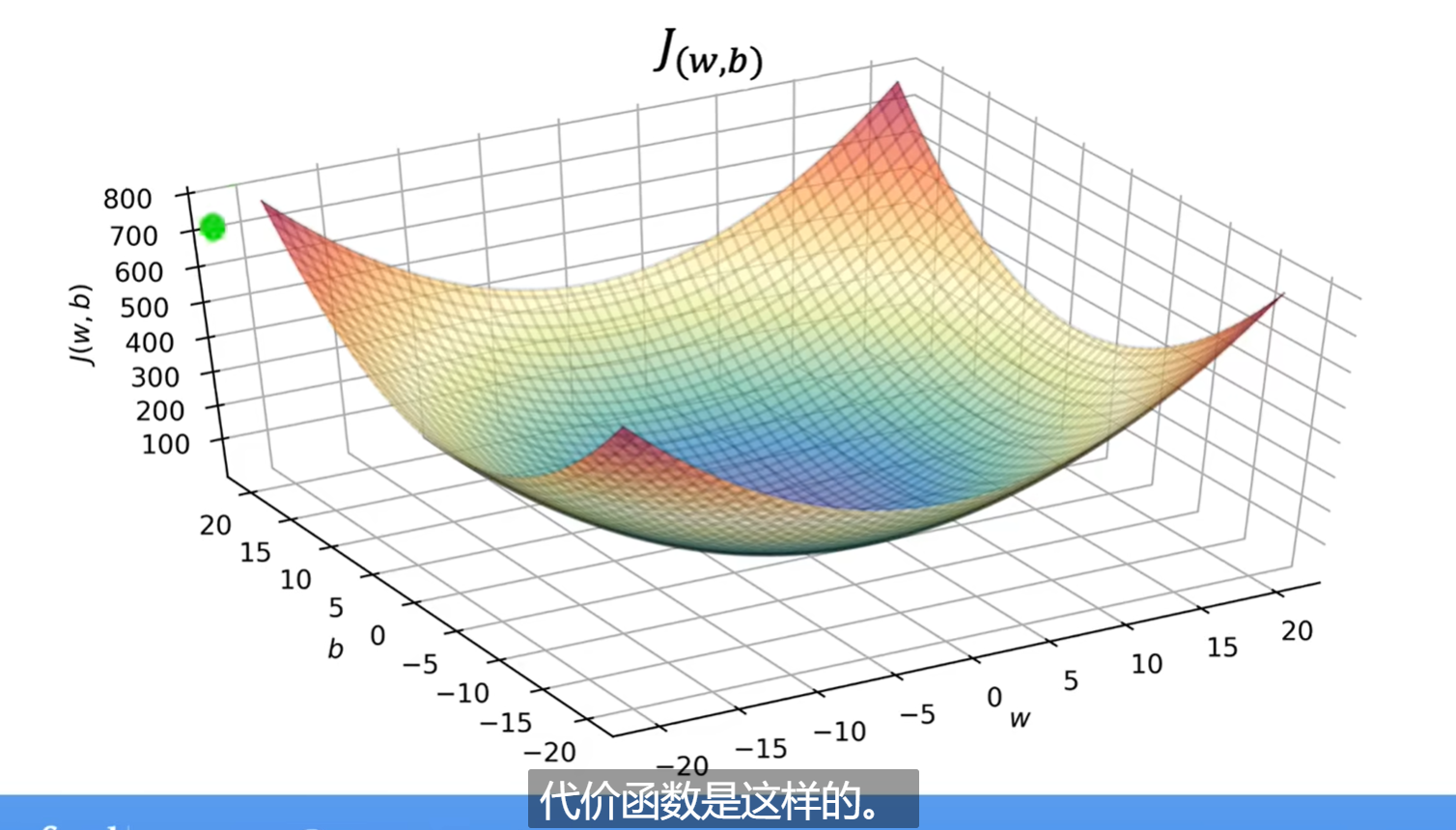
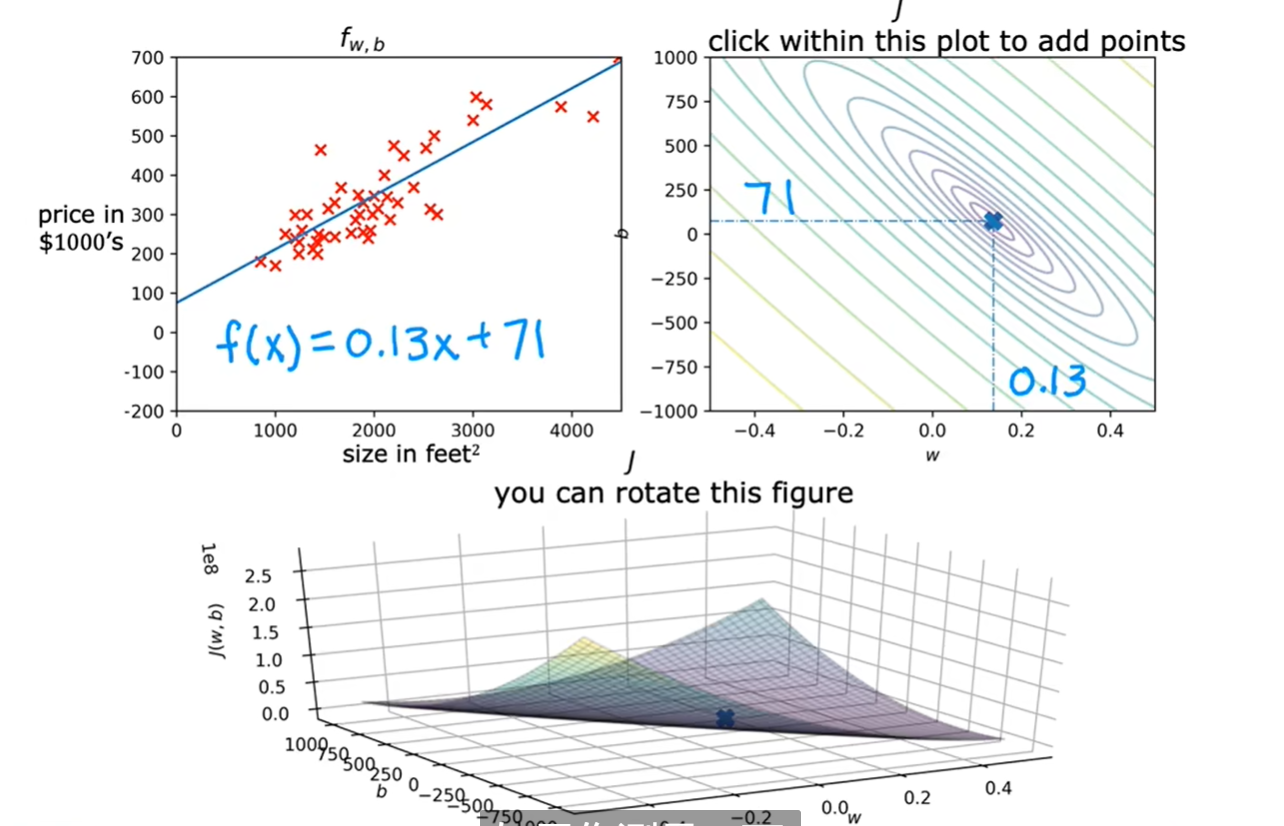
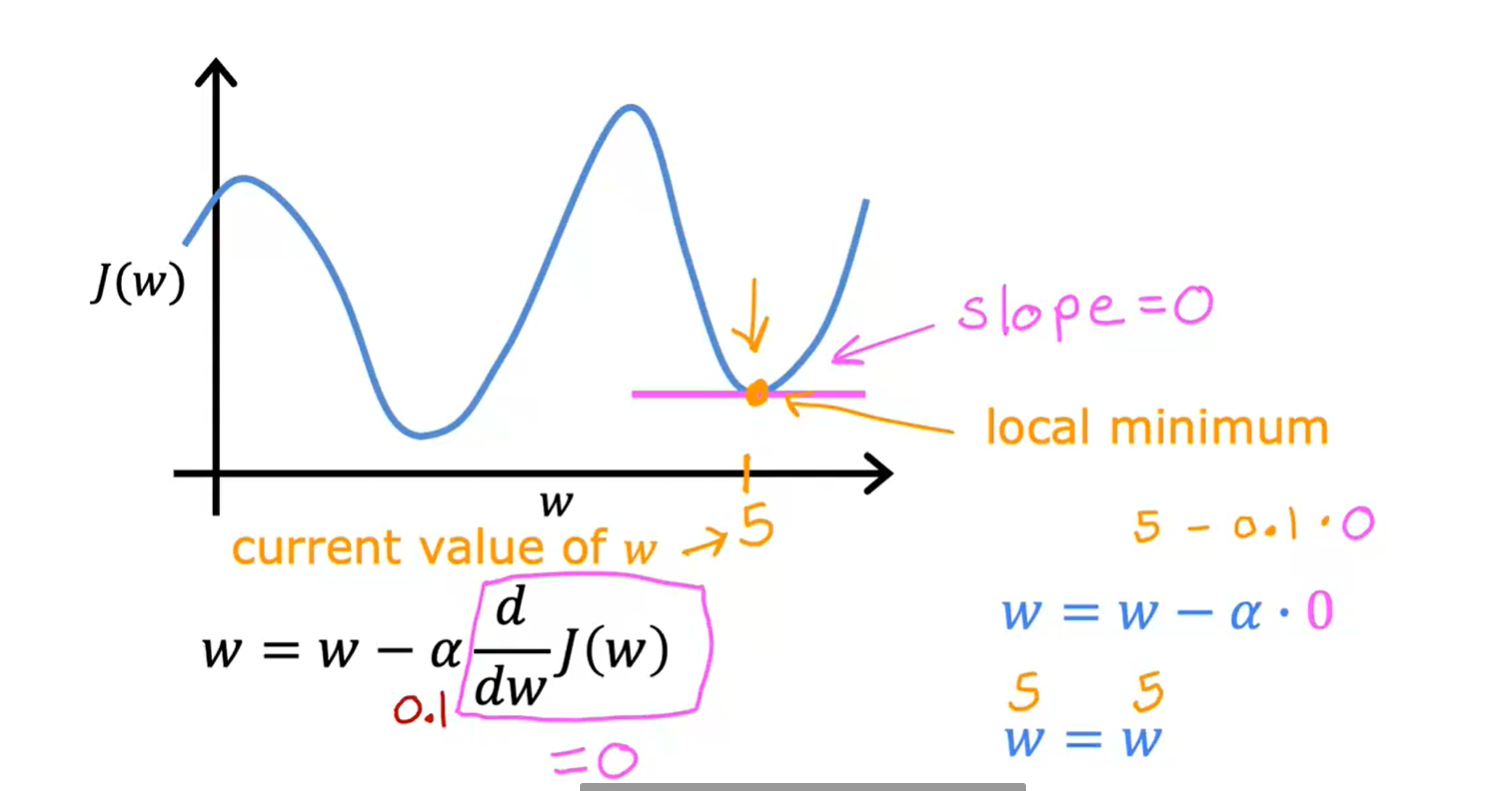
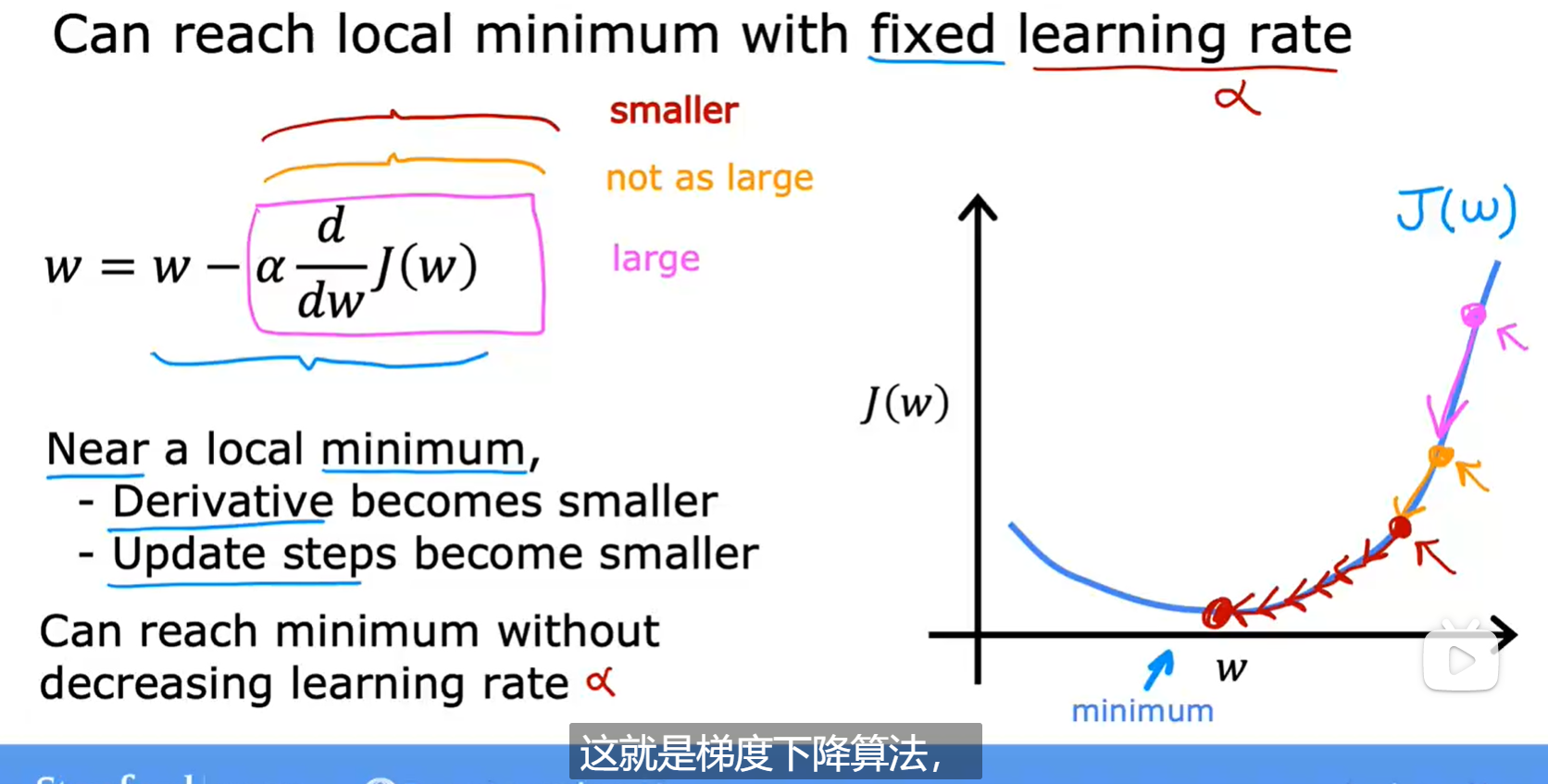
4. 梯度下降
梯度下降参考博客:梯度下降(Gradient Descent)小结
梯度下降法(Grandient descent)

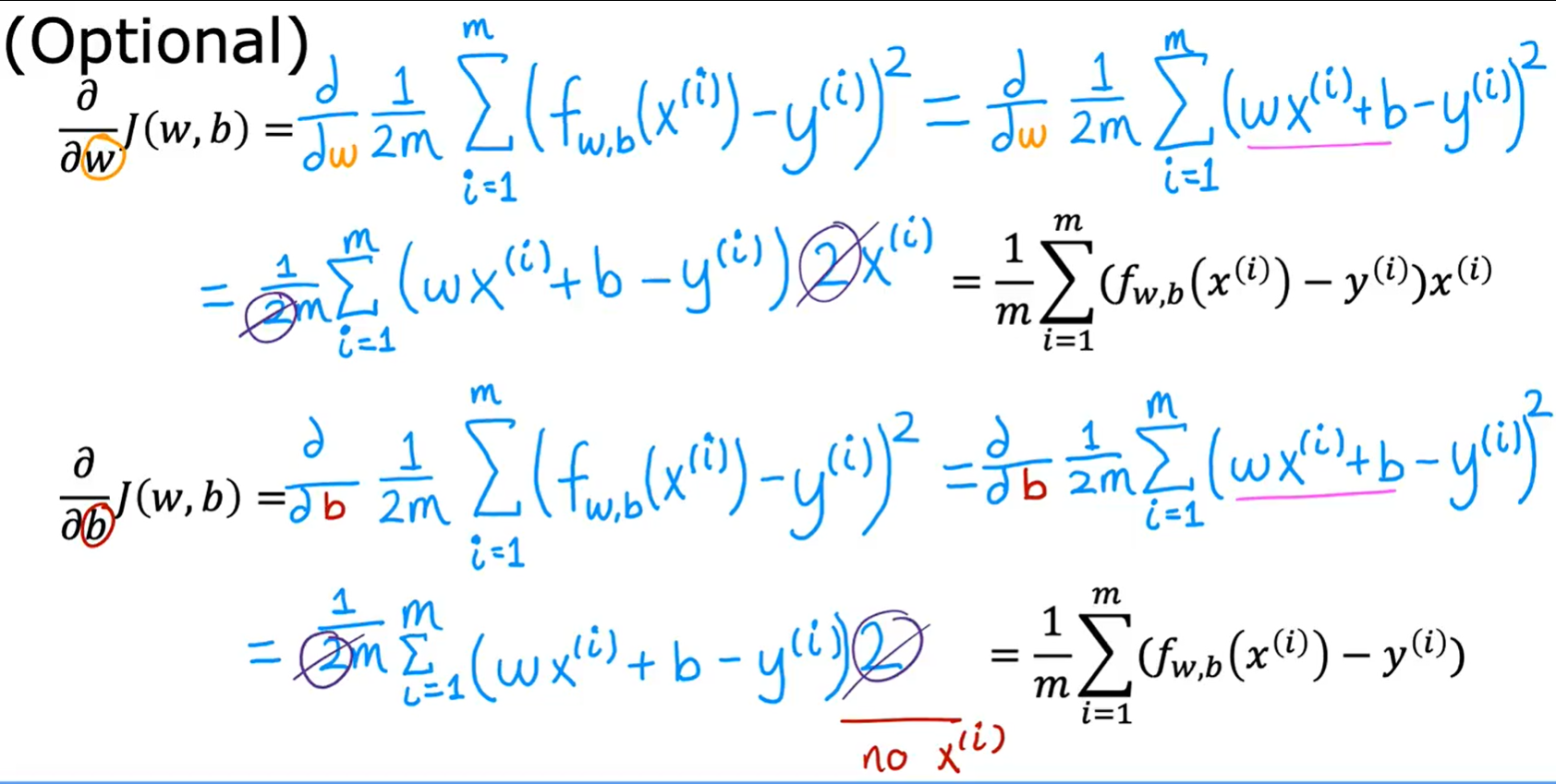
f函数的计算如下:
# Function to calculate the cost:算出代价
def compute_cost(x, y, w, b):
m = x.shape[0] //m是x的行数,array.shape[0]是行数,array.shape[1]是列数
cost = 0
for i in range(m):
f_wb = w * x[i] + b
cost = cost + (f_wb - y[i])**2
total_cost = 1 / (2 * m) * cost
return total_cost
求偏导:
def compute_gradient(x, y, w, b):
"""
Computes the gradient for linear regression
Args:
x (ndarray (m,)): Data, m examples
y (ndarray (m,)): target values
w,b (scalar) : model parameters
Returns
dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
dj_db (scalar): The gradient of the cost w.r.t. the parameter b
"""
# Number of training examples
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x[i] + b
dj_dw_i = (f_wb - y[i]) * x[i]
dj_db_i = f_wb - y[i]
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
梯度下降函数:
def gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):
"""
Performs batch gradient descent to learn theta. Updates theta by taking
num_iters gradient steps with learning rate alpha
Args:
x : (ndarray): Shape (m,)
y : (ndarray): Shape (m,)
w_in, b_in : (scalar) Initial values of parameters of the model
cost_function: function to compute cost
gradient_function: function to compute the gradient
alpha : (float) Learning rate
num_iters : (int) number of iterations to run gradient descent
Returns
w : (ndarray): Shape (1,) Updated values of parameters of the model after
running gradient descent
b : (scalar) Updated value of parameter of the model after
running gradient descent
"""
# number of training examples
m = len(x)
# An array to store cost J and w's at each iteration — primarily for graphing later
J_history = []
w_history = []
w = copy.deepcopy(w_in) #avoid modifying global w within function
b = b_in
for i in range(num_iters):
# Calculate the gradient and update the parameters
dj_dw, dj_db = gradient_function(x, y, w, b )
# Update Parameters using w, b, alpha and gradient
w = w - alpha * dj_dw
b = b - alpha * dj_db
# Save cost J at each iteration
if i<100000: # prevent resource exhaustion
cost = cost_function(x, y, w, b)
J_history.append(cost)
# Print cost every at intervals 10 times or as many iterations if < 10
if i% math.ceil(num_iters/10) == 0:
w_history.append(w)
print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")
return w, b, J_history, w_history #return w and J,w history for graphing
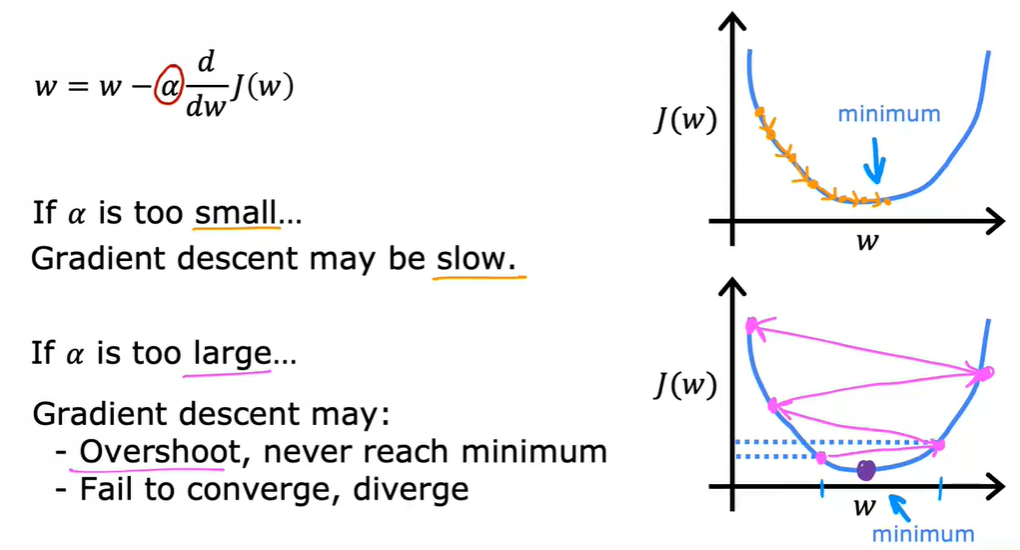
4.1 学习率
学习率太小可能迭代过慢
学习率太大可能不收敛,甚至发散



 浙公网安备 33010602011771号
浙公网安备 33010602011771号