5. bn和ln

batchnormalization和layernormalization，主要区别在于 normalization的方向不同。

normalization

Normalization：规范化或标准化，就是把输入数据X，在输送给神经元之前先对其进行平移和伸缩变换，将X的分布规范化成在固定区间范围的标准分布。

Normalization 的作用很明显，把数据拉回标准正态分布，因为神经网络的Block大部分都是矩阵运算，一个向量经过矩阵运算后值会越来越大，为了网络的稳定性，我们需要及时把值拉回正态分布。

bn和ln的区别

Batchnorm 顾名思义是对一个batch进行操作。假设我们有 10行 3列 的数据，即我们的batchsize = 10，每一行数据有三个特征，假设这三个特征是【身高、体重、年龄】。那么BN是针对每一列（特征）进行缩放，例如算出【身高】的均值与方差，再对身高这一列的10个数据进行缩放。体重和年龄同理。这是一种“列缩放”。

而layer方向相反，它针对的是每一行进行缩放。即只看一笔数据，算出这笔所有特征的均值与方差再缩放。这是一种“行缩放”。

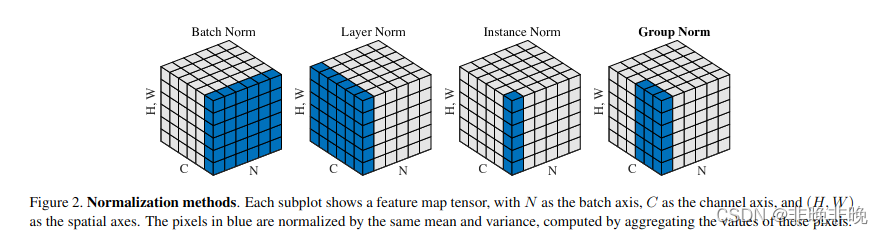
可以看出，layer normalization 对所有的特征进行缩放，这显得很没道理。我们算出一行这【身高、体重、年龄】三个特征的均值方差并对其进行缩放，事实上会因为特征的量纲不同而产生很大的影响。但是BN则没有这个影响，因为BN是对一列进行缩放，一列的量纲单位都是相同的。

BN抹杀了不同特征之间的大小关系，但是保留了不同样本间的大小关系；LN抹杀了不同样本间的大小关系，但是保留了一个样本内不同特征之间的大小关系。（理解：BN对batch数据的同一特征进行标准化，变换之后，纵向来看，不同样本的同一特征仍然保留了之前的大小关系，但是横向对比样本内部的各个特征之间的大小关系不一定和变换之前一样了，因此抹杀或破坏了不同特征之间的大小关系，保留了不同样本之间的大小关系；LN对单一样本进行标准化，样本内的特征处理后原来数值大的还是相对较大，原来数值小的还是相对较小，不同特征之间的大小关系还是保留了下来，但是不同样本在各自标准化处理之后，两个样本对应位置的特征之间的大小关系将不再确定，可能和处理之前就不一样了，所以破坏了不同样本间的大小关系）

在BN和LN都能使用的场景中，BN的效果一般优于LN，原因是基于不同数据，同一特征得到的归一化特征更不容易损失信息。但是有些场景是不能使用BN的，例如batch size较小或者序列问题中可以使用LN。这也就解答了RNN 或Transformer为什么用Layer Normalization？

Transformer为什么用layernorm

首先RNN或Transformer解决的是序列问题，一个存在的问题是不同样本的序列长度不一致，而Batch Normalization需要对不同样本的同一位置特征进行标准化处理，所以无法应用；当然，输入的序列都要做padding补齐操作，但是补齐的位置填充的都是0，这些位置都是无意义的，此时的标准化也就没有意义了。

其次上面说到，BN抹杀了不同特征之间的大小关系；LN是保留了一个样本内不同特征之间的大小关系，这对NLP任务是至关重要的。对于NLP或者序列任务来说，一条样本的不同特征，其实就是时序上的变化，这正是需要学习的东西自然不能做归一化抹杀，所以要用LN。

代码

batchnorm

class BatchNorm1d(_BatchNorm):
    def _check_input_dim(self, input):
        if input.dim() != 2 and input.dim() != 3:
            raise ValueError('expected 2D or 3D input (got {}D input)'
                             .format(input.dim()))

layernorm

class LayerNorm(torch.nn.Module):
    def __init__(self,
                 dimension: int,
                 eps: float = 1e-6) -> None:
        super().__init__()
        self.gamma = torch.nn.Parameter(torch.ones(dimension))
        self.beta = torch.nn.Parameter(torch.zeros(dimension))
        self.eps = eps

    def forward(self, tensor: torch.Tensor):  # pylint: disable=arguments-differ
        # 注意，是针对最后一个维度进行求解~
        mean = tensor.mean(-1, keepdim=True)
        std = tensor.std(-1, unbiased=False, keepdim=True)
        return self.gamma * (tensor - mean) / (std + self.eps) + self.beta