Lecture 2: Data Sampling and Probability
详细地址:data100Lecture2
1. 引
1.1 图表的使用
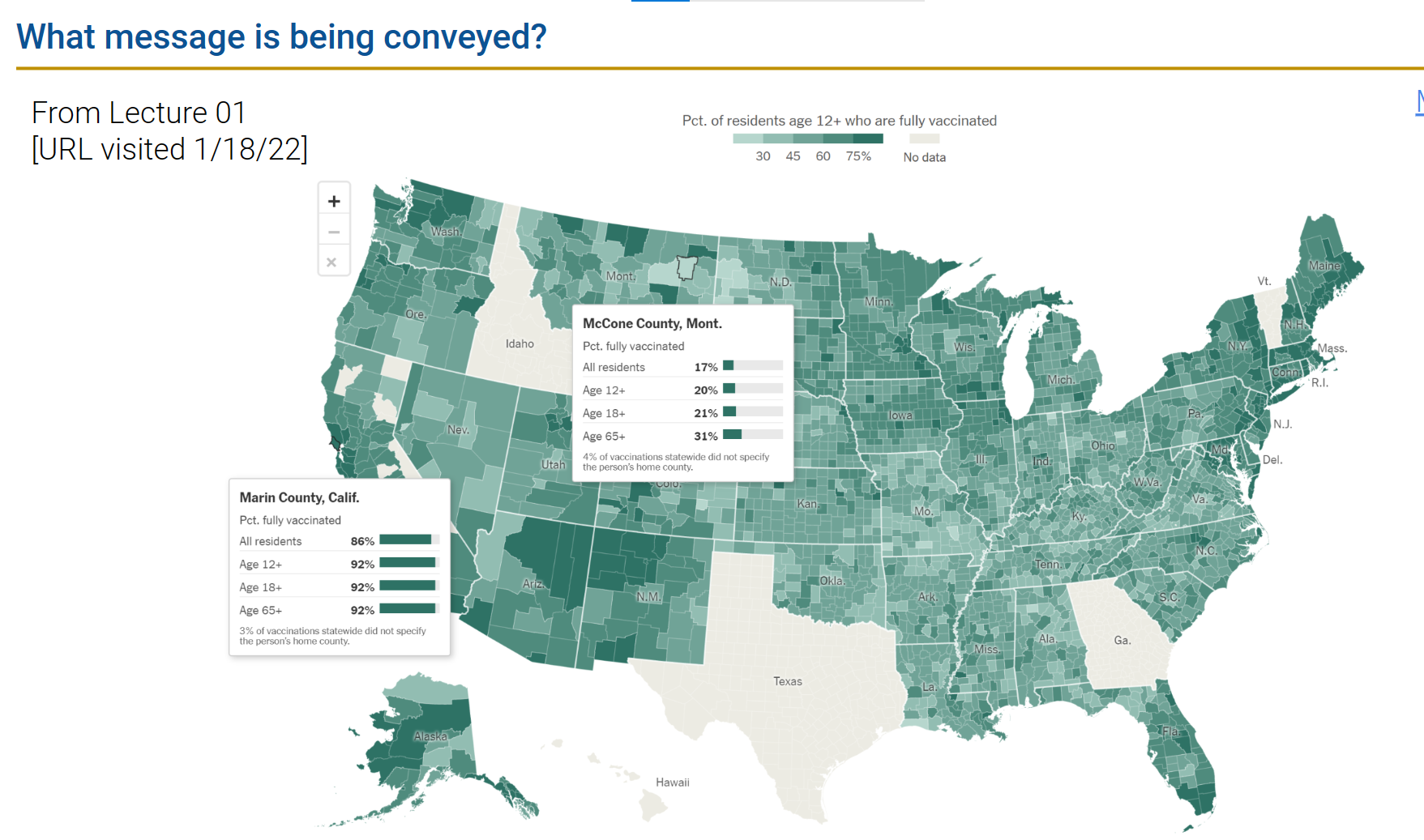
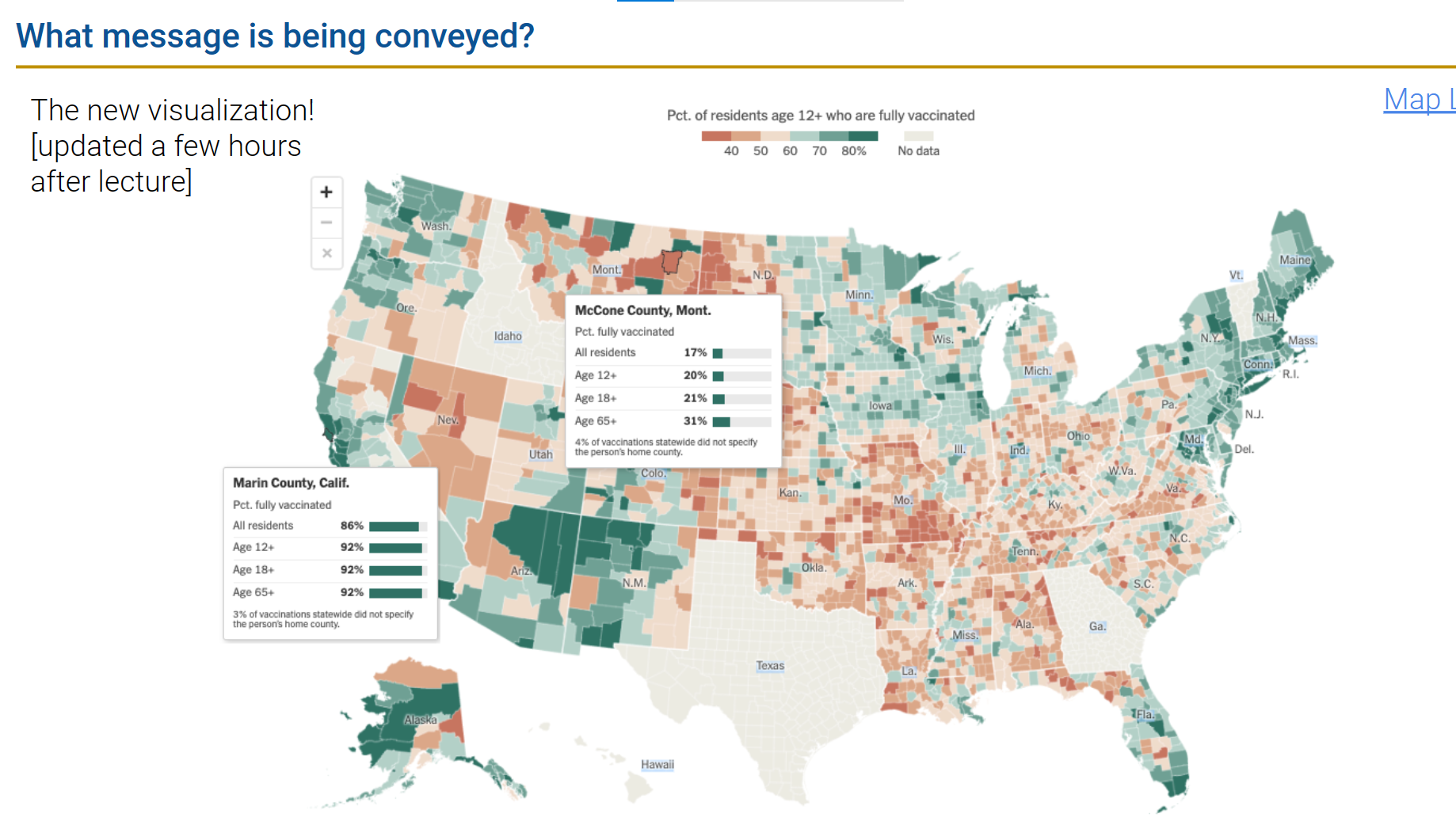
两张图片基于相同数据生成,但是表达的意思、想突出的重点完全不一样
1.2 数据科学生命周期
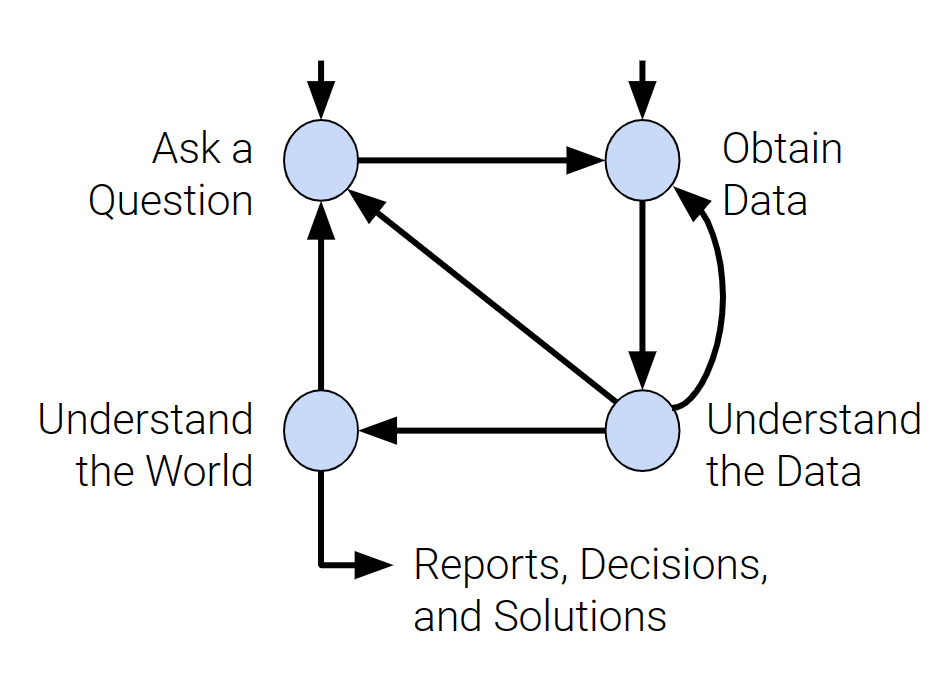
上图是数据科学生命周期,这节课就将如何收集数据
2. 人口普查和调查
- 可能会有许多误差,有的人无家可归等等,需要理解数据
3. 取样:定义
- A sample is a subset of the population.样本通常用于推断群体。
- 常见的两种误差:
- 偶然误差:随机样本可能 在任何方向上都可能与预期不同。
- 偏差:一个方向上的系统误差。
无论使用什么方法取样,所推断的结果与实际总有偏差
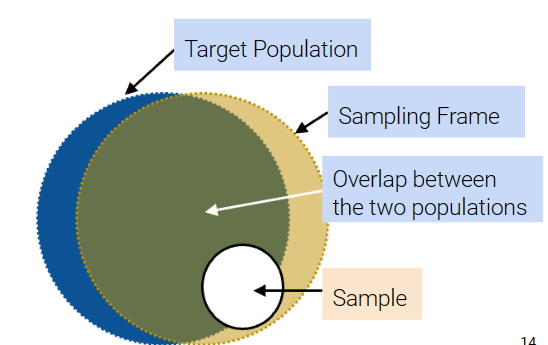
- sampling frame:抽样框架,即从中抽样的名单,最终可能出现在样本中的人的集合
- sample:实际抽取的样本
4. 偏差:案例研究
- 选择偏差
- 系统地排除(或偏袒)特定群体。
- 如何避免?检查抽样框架和抽样方法。
- 回应偏差
- 人们的回答并不总是真实的。
- 如何避免?检查问题的性质和调查方法。
- 非响应偏差
- 人们并不总是做出回应。
- 如何避免?调查要简短,要坚持不懈。
- 不回复的人和回复的人不一样!
5. 概率样本
5.1 常见的非随机样本:
方便样本
- 方便样本就是你能找到的人。
- 对于推论来说,这不是个好主意!
- 随意≠随机。
- 偏见的来源可能会以你想不到的方式出现!
配额样本
配额样本是指您首先指定您所希望的各种子群体的细分,然后尽可能达到这些目标。
例如: 您想对本镇的个人进行抽样,并希望抽样的年龄分布与本镇的人口普查结果一致。
- 无论如何 "达到配额都不是随机的。
- 您的样本会在某些方面与人口相似,但不是全部。
- 年龄配额将代表年龄。那么性别呢?种族?各区域居住的人数?
5.2 常见的随机抽样方案
带替换的随机抽样
带替换的随机抽样是指均匀地随机抽取样本,并进行替换。
随机并不总是指 "均匀随机",但在这种特定情况下,它确实指 "均匀随机"。
简单随机抽样
简单随机抽样(simple random sample,SRS)是指不带替换的均匀随机抽样。
每个个体(以及个体的子集)被选中的几率相同。每一对个体与其他每一对个体的被选机会相同。每个三元组与其他三元组的机会相同。
以此类推。
- 案例分析:考虑以下抽样方案:一个班级的花名册上有 1100 名学生,按字母顺序排列。从名单上的前 10 名学生中随机抽取一名。在创建样本时,选取该学生和之后列出的每 10 个学生(如第 8、18、28、38 等学生)。
- 这是概率抽样吗?是的
- 每个学生被抽中概率是否相同?是的
- 是否是简单随机抽样?不是,{8,9,...}与{8,18,...}被抽中的概率显然不同
5.3 数据科学中常见的一种情况
我们有庞大的人口,但只能对相对较少的个体进行采样。
如果与样本相比,人口数量庞大,那么
带替换和不带替换的随机抽样几乎是一样的。
- 举例说明: 假设人口中有 10,000 人。其中正好有 7500 人喜欢小吃 1,另外 2500 人喜欢小吃 2。在 20 个随机样本中,所有人都喜欢小吃 1 的概率是多少?

6. 公式
如果我们从一个分为三个不同类别(其中 p1 + p2 + p3 = 1)的群体中随机替换抽取 n 次,我们可以得到以下结果
第 1 类,比例为 p1 的个体。第 2 类,比例为 p2 的个体。第 3 类,比例为 p3 的个体。
那么,从第 1 类中抽取 k1 个个体、从第 2 类中抽取 k2 个个体、从第 3 类中抽取 k3 个个体(其中 k1 + k2 + k3 = n)的多项式概率为
\[\frac{n!}{k_1}
\]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号