2.3 搜索与图论（最小生成树和二分图）

 

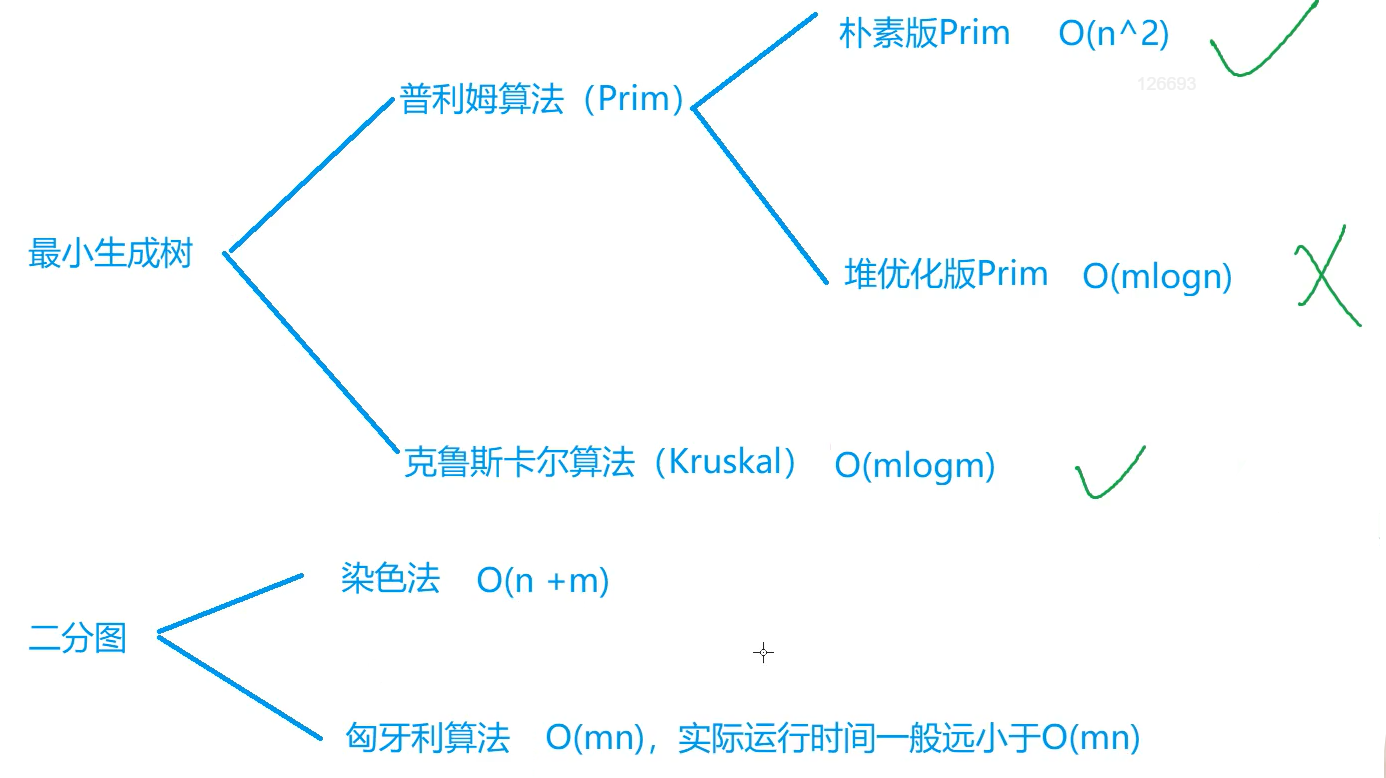
 1. 朴素版Prim算法

跟朴素dijkstra有点像，但是每次更新的是每个点到已收录的点的集合的距离，而不是到起点的距离。

先迭代n次，每次找到距离集合距离最小的点，将其收录、更新res，然后用其更新其余点到集合的距离

代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510 , INF = 0x3f3f3f3f;
int g[N][N] , dist[N];
bool st[N];
int n , m;

int prim()
{
    memset(dist , 0x3f , sizeof dist);
    
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1 ; j <= n ; j ++)
            if (!st[j] and (t == -1 or dist[j] < dist[t]))
                t = j;
        
        st[t] = true;
        if (i and dist[t] == INF) return INF;  //如果不是第一次遍历并且该点到集合的距离为无穷
        if (i) res += dist[t];
        
        for (int j = 1 ; j <= n ; j ++)  //更新其余点到集合的距离
            dist[j] = min(dist[j] , g[t][j]);
    }
    return res;
}

int main()
{
    cin >> n >> m;
    memset(g , 0x3f , sizeof g);
    
    while (m -- )
    {
        int a , b , c;
        scanf("%d%d%d" , &a , &b , &c);
        g[a][b] = g[b][a] = min(g[a][b] , c);  //无向图
    }
    
    int t = prim();
    
    if (t == INF) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

2. Kruskal算法

要用到并查集的知识。将所有边储存起来，按照边的权重进行排序，每次取出最短的边，如果两个端点不同，就将该边读入，记录读入的点的数量的cnt++

最终如果cnt < n - 1，说明有点没有读入，输出impossible

代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010;
int p[N];
struct Edge{
    int a , b , c;
    bool operator < (const Edge & t) const  //重载小于号
    {
        return c < t.c;
    }
}edges[N];

int n , m;

int find(int x)  //并查集find
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    
    for (int i = 1 ; i <= n ; i ++) p[i] = i;
    for (int i = 0 ; i < m ; i ++)
    {
        int a , b , c;
        scanf("%d%d%d" , &a , &b , &c);
        edges[i] = {a , b , c};  //储存所有边
    }
    
    sort(edges , edges + m);  //将所有边按权重排序
    
    int res = 0 , cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        auto t = edges[i];
        int a = find(t.a) , b = find(t.b) , c = t.c;
        
        if (a != b)  //每次找出最短的边，如果二者祖宗节点不同
        {
            res += c;
            cnt ++;
            p[a] = b;
        }
    }
    if (cnt < n - 1) puts("impossible");  //如果读入的点少于n - 1个
    else cout << res << endl;
    
    return 0;
}

3. 二分图

二分图当且仅当图中没有奇数环

3.1 染色法求二分图

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010;
int h[N] , e[M] , ne[M] , idx;
int color[N];  //染色，1 or 2
int n , m;

void add(int a , int b)
{
    e[idx] = b , ne[idx] = h[a] , h[a] = idx ++;
}

bool dfs(int u , int t)
{
    color[u] = t;  //要染色！
    for (int i = h[u] ; i != -1 ; i = ne[i])
    {
        int j = e[i];
        if (!color[j])
        {
            if (!dfs(j , 3 - t)) return false;  //如果该点染色失败
        }
        if (color[j] == t) return false;  //如果该点跟u点颜色一样
    }
    return true;
}


int main()
{
    cin >> n >> m;
    memset(h , -1 , sizeof h);
    
    while (m -- )
    {
        int a , b;
        scanf("%d%d" , &a , &b);
        add(a , b) , add(b , a);  //无向图
    }
    bool flag = true;
    for (int i = 1 ; i <= n ; i ++)
    {
        if (!color[i])
        {
            if (!dfs(i , 1))
            {
                flag = false;
                break;
            }
        }
    }
    if (flag) puts("Yes");
    else puts("No");
    return 0;
}