背包问题

 1.0-1背包问题

f[i][j]表示在前 i 个物品中进行选择，其中物品体积不超过 j 的所有物品的最大的价值，每个f [i][j]可以分为两部分，一是不包含第 i 个物品的选择， 那这种情况下f[i][j]就等于 f[i-1][j]；二是包含第 i 个物品的选择，这种情况只有 j > v[i]才会触发，此时 如果包含第 i 个物品的f[i][j] = f[i - 1] [j - v[i]] + w[i]，只选 i - 1个物品并且最大体积不超过 j - v[i]，第二种情况算完之后要比较两种选择哪个较大，储存较大的值，把第二种情况的两步合起来写就是

if (j > v[i]) f[i][j] = max(f[i-1][j] , f[i-1][j-v[i]] + w[i]);//由于在第一种情况已经把f[i][j] =  f[i-1][j]了，所以此处的 f[i-1][j]也可以写f[i][j]

代码如下

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int v[N] , w[N];
int n , m;
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1 ; i <= n ; i++) cin >> v[i] >> w[i];
    for (int i = 1 ; i <= n ; i++)
        for (int j = 0 ; j <= m ; j++)
        {
            f[i][j] = f[i-1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j] , f[i-1][j-v[i]]+w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

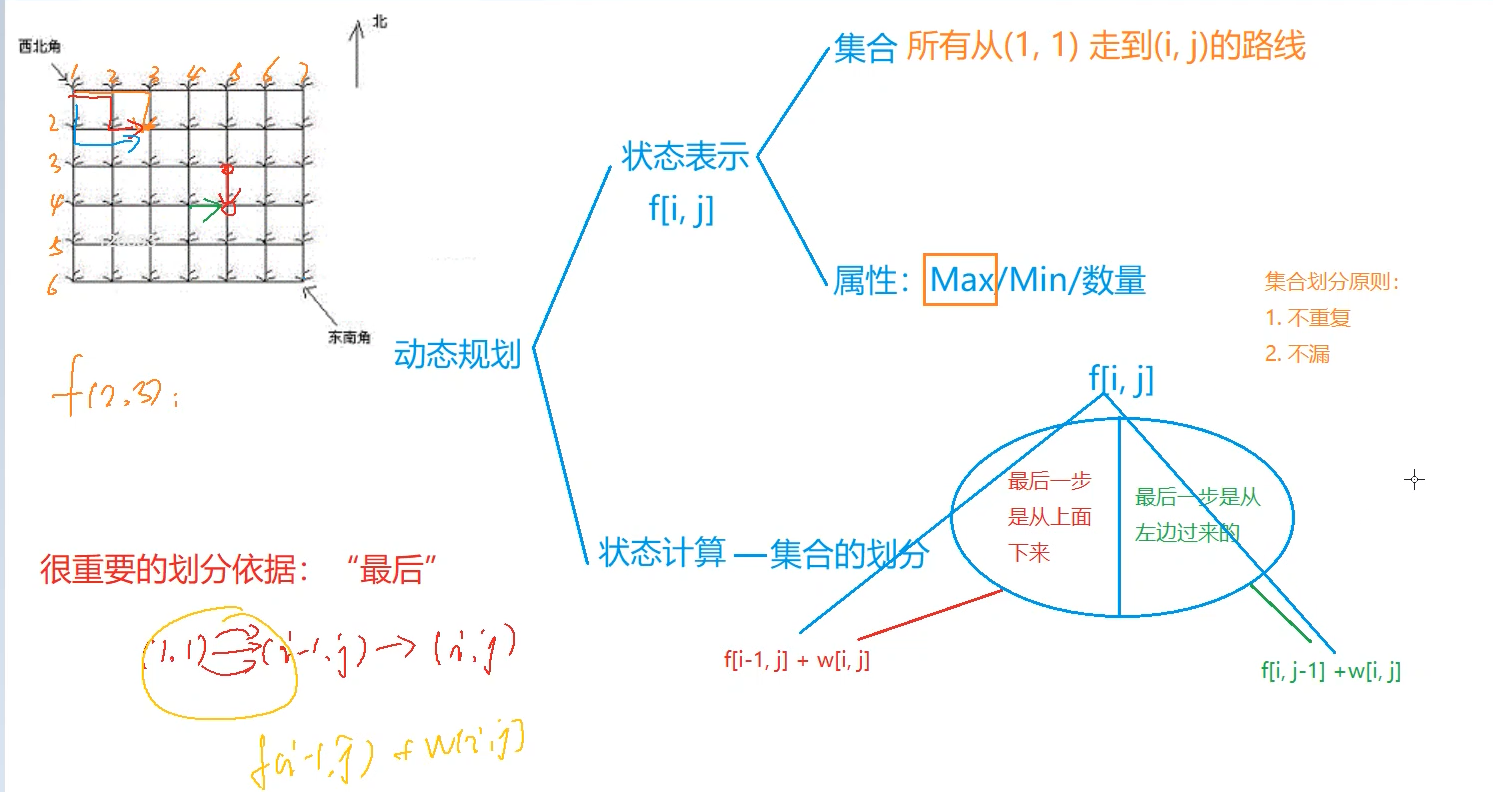
2.DP分析思路