2.3搜索与图论

 1.dfs

n皇后问题 

#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
int col[N] , dg[N] , udg[N];//列，正对角线，斜对角线

void dfs(int u){
    if(u==n){
        for(int i = 0 ; i < n ; i++) puts(g[i]);
        puts("");
        return;
    }
    for(int i = 0 ; i < n ; i++){
        if(!col[i] and !dg[i-u+n] and !udg[i+u]){//u是x ， i是y
            g[u][i] = 'Q';
            col[i] = dg[i-u+n] = udg[i+u] = 1;
            dfs(u+1);
            col[i] = dg[i-u+n] = udg[i+u] = 0;
            g[u][i] = '.';//恢复现场
        }
    }
}

int main(){
    scanf("%d" , &n);
    for(int i = 0 ; i < n; i ++){
        for(int j = 0 ; j < n ; j++){
            g[i][j] = '.';
        }
    }
    dfs(0);
    return 0;
}

 还有更为通用的办法，但是慢很多

#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
int row[N] , col[N], dg[N] , udg[N];

void dfs(int x , int y , int k){
    if(y>=n) y = 0 , x++;
    if(x==n){
        if(k==n){
            for(int i = 0 ; i < n ; i++) puts(g[i]);
            puts("");
        }
        return;
    }//注意return顺序
    
    //不放皇后
    dfs(x,y+1,k);
    
    //放皇后
    if(!row[x] and !col[y] and !dg[n+y-x] and !udg[x+y]){
        g[x][y] = 'Q';
        row[x] = col[y] = dg[n+y-x] = udg[x+y] = 1;
        dfs(x,y+1,k+1);
        row[x] = col[y] = dg[n+y-x] = udg[x+y] = 0;
        g[x][y] = '.';
    }
}

int main(){
    scanf("%d" , &n);
    for(int i = 0 ; i < n ; i++){
        for(int j  = 0 ; j < n ; j++){
            g[i][j] = '.';
        }
    }
    dfs(0 ,0 , 0);
    return 0;
}

2.BFS  解所有边的权重相同的最短路问题

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;

const int N = 110;
typedef pair<int,int> PII;
int n , m;
int g[N][N] , d[N][N];//g存原图，d存每个点至起点的距离

int bfs(){
    queue<PII> q;
    
    memset(d,-1,sizeof d);
    d[0][0] = 0;
    q.push({0,0});
    
    int dx[] = {-1,0,1,0} , dy[] = {0,1,0,-1};
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        for(int i = 0 ; i < 4 ; i++){
            int x = t.first+dx[i] , y = t.second+dy[i];
            if(x>=0 and x<n and y>=0 and y<m and g[x][y]==0 and d[x][y]==-1){
                d[x][y] = d[t.first][t.second]+1;
                q.push({x,y});
            }
        }
    }
    return d[n-1][m-1];
}

int main(){
    cin>>n>>m;
    for(int i = 0 ; i < n ; i++){
        for(int j = 0 ; j < m ; j++){
            cin>>g[i][j];
        }
    }
    cout<<bfs()<<endl;
    return 0;
}

八数码问题

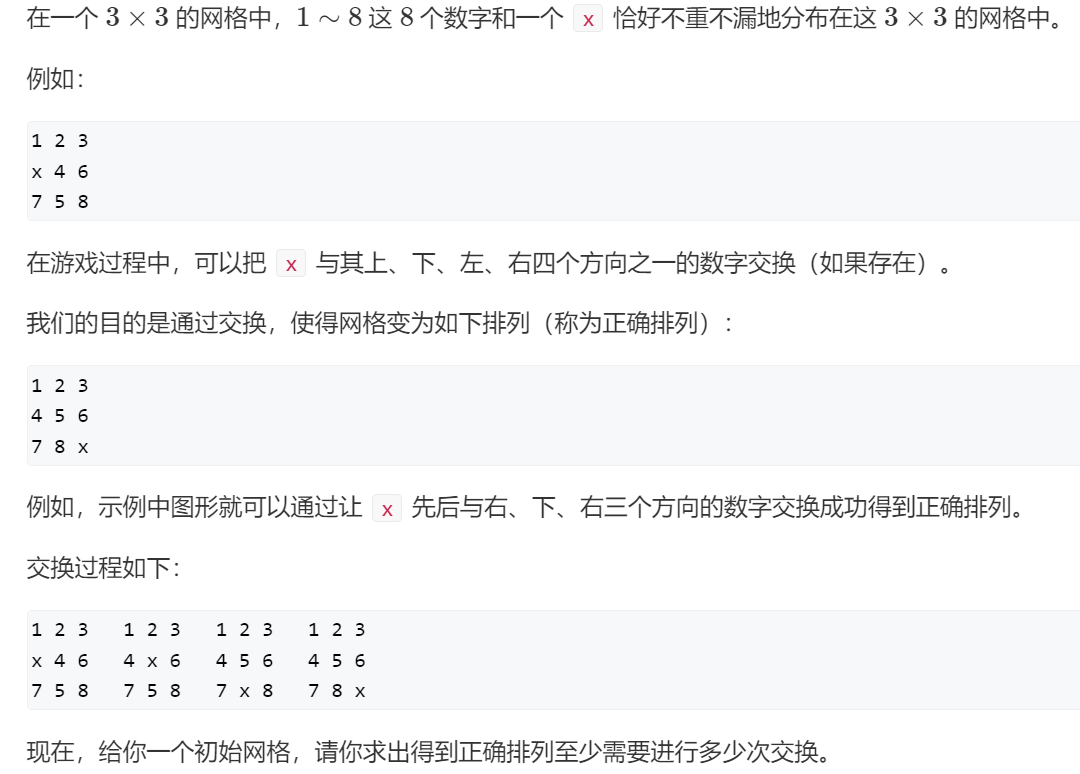
就是数字版华容道，先用string储存原始状态，用queue<string>创队列，用unordered_map<string,int>储存每个状态以及其用的步数，用t表示弹出的队头，用k表示队头状态中x所在的位置，用dx[]、dy[]表示上下左右移动，用swap交换x与所要移动的数字，如果unordered_map中没有新得到的这个状态，就将此状态加入队伍与哈希表

//https://www.acwing.com/problem/content/847/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;

int bfs(string start)
{
    string end = "12345678x";
    queue<string> q;
    unordered_map<string , int> p;
    q.push(start);
    p[start] = 0;

    int dx[] = {-1, 0 , 1 , 0} , dy[] = {0 , 1 , 0 , -1};
    while(q.size())
    {
        auto t = q.front();//取出队头
        q.pop();

        int distance = p[t];
        if(t==end) return distance;

        int k = t.find('x');//找出x所在位置
        int x = k/3 , y = k%3;
        for(int i = 0 ; i < 4 ; i++)
        {
            int a = x + dx[i] , b = y + dy[i];
            if(a >= 0 and a < 3 and b >= 0 and b < 3)
            {
                swap(t[k] , t[a*3+b]);
                if(!p.count(t))
                {
                    q.push(t);
                    p[t] = distance +1 ;
                }               
                swap(t[k] , t[a*3+b]);//还原现场
            }
        }
    }
    return -1;//没有找到与end相同的结果，返回-1
}

int main()
{
    string start;//记录初始数据
    for(int i = 0 ; i < 9 ; i++)
    {
        char c;
        cin>>c;
        start+=c;
    }
    cout << bfs(start) << endl;
    return 0;
}

（最近听了郝斌老师的C语言教程，尝试把代码写的规范一点，虽然还是不太规范）

3.图或者表的dfs搜索

//https://www.acwing.com/problem/content/description/848/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5+10 , M = 2*N;
int n;
int h[N] , e[M] , ne[M] , idx;
bool st[N];
int ans = N;//最终答案，即去掉重心剩下的最少的点数

void add(int a , int b){
    e[idx] = b , ne[idx] = h[a] , h[a] = idx++;
}

int dfs(int u){
    int sum = 1 , res = 0;//sum是以u点为根节点的点数和,res是删掉u后最大的可以连接的节点数
    st[u] = true;//标记一下u点已经搜过了
    for(int i = h[u] ; i!=-1 ; i = ne[i]){
        int j = e[i];
        if(!st[j]){//如果没有被搜过
            int s = dfs(j);
            res = max(res , s);//删掉某个点A后最大的可以连接的点数就是以该A点直接连接的某点B为根的点数和(1)
            sum+=s;
        }
    }
    res = max(res , n - sum);//(1)或者n-该点数和
    ans = min(ans , res);
    return sum;
}

int main(){
    cin>>n;
    memset(h , -1 , sizeof h);//让表头指向-1

    for(int i = 0 ; i < n ; i++){
        int a , b;
        cin>>a>>b;
        add(a,b);
        add(b,a);//没有箭头，所以加双向箭头
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

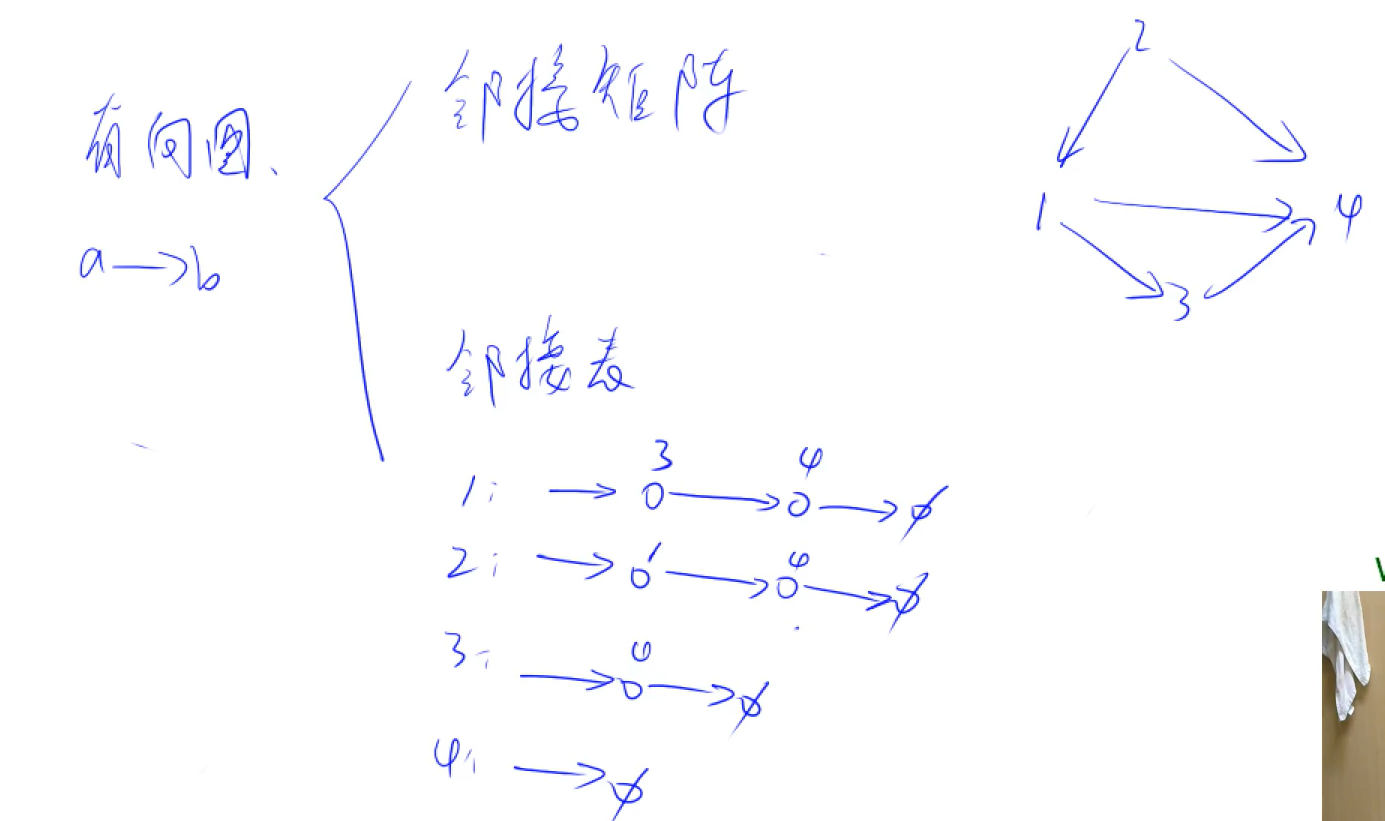
4.图的宽搜最经典的应用就是拓扑序列

拓扑序列针对的是有向图，对于拓扑序列当我们把其中的点排列好后，其所有边都是从前指到后的（拓扑序列不会有环，有向无环图也被称为拓扑图，如果一个图存在环，则环上的所有点都进不了拓扑序列）。

拓扑图每个点都有入度及出度，就是指向该点的点的数量、该点指向的点的数量

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100010;
int n , m;
int h[N] , e[N] , ne[N] , idx;
int q[N] , d[N];

void add(int a , int b){
    e[idx] = b , ne[idx] = h[a] , h[a] = idx++;
}

bool topsort(){
    int hh = 0 , tt = -1;
    for(int i = 1 ; i <= n ; i++){
        if(d[i]==0) q[++tt] = i;
    }
    
    while(hh<=tt){
        int t = q[hh++];//取出队头
        for(int i = h[t] ; i!=-1 ; i = ne[i]){
            int j = e[i];
            d[j]--;
            if(d[j]==0) q[++tt] = j;
        }
    }
    return tt+1==n;//判断是否所有元素入队
}

int main(){
    cin>>n>>m;
    memset(h , -1 , sizeof h);
    
    while(m--){
        int a, b;
        cin>>a>>b;
        add(a,b);
        d[b]++;
    }
    if(topsort()){
        for(int i = 0 ; i < n ; i++) printf("%d " , q[i]);
    }
    else puts("-1");
    
    return 0;
}