概率论复习笔记（1 - 12）

01 样本空间与随机事件 略 没必要

02 事件的关系和运算：

 

 

 对偶律值得注意一下

03 概率的定义和性质

 

 

 

 

 

 虽然这部分我都略了 但是基础还是不能忽视 要结合一些课后题巩固 只不过在这里没有着重整理的必要 因为是人都要会这些的

04古典概型和几何概型

其实多数是中学时代的内容 当然也有一些难题和偏题 但是这部分毕竟也不是重点

想要满分可以去一冲 

05 条件概率

 

 

 （在谁的条件下就要除以谁的概率）

06 概率的五大公式

 

 

 

 

 

还是要做题体会的 题目做多了一看就知道是用全概率公式还是贝叶斯

07 事件的独立性：

 

独立的性质：

 

 

 

 

 

 08 独立重复实验

 

 

 

 

09 随机变量与分布函数：

随机变量：把样本点数值化

 

 

 

 

 

 

 分布函数的性质：

 

 自己推就能推出来

 

10 离散型随机变量及其分布：

 

分布函数阶梯化：

 

 

 11 连续型随机变量

 

 

 

 12 常见分布 

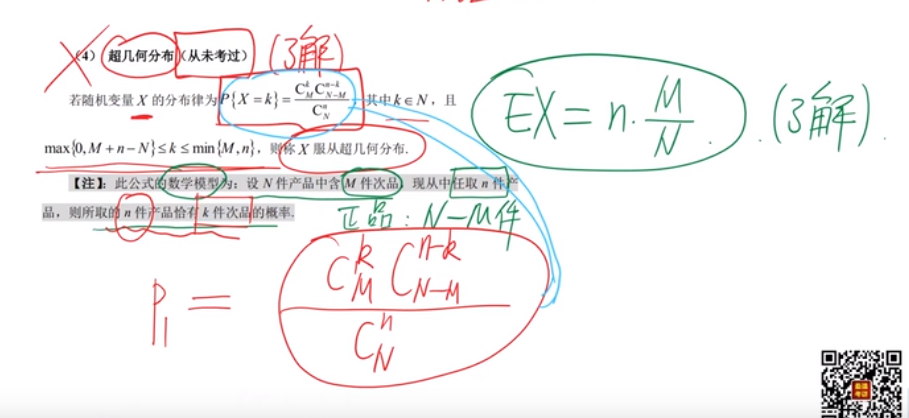
考研从没考过超几何分布 八种常见分布其实只有七种

 

 可是数一大纲有超几何分布 是个冷门考点 有可能翻车的

常见的离散型随机变量分布：

（期望和方差图中都画了）

 

 要记住相应符号 表示 分布律 期望方差 背过

几何分布：

 

 

 

二项分布更重要点

超几何分布

 

 泊松分布

 

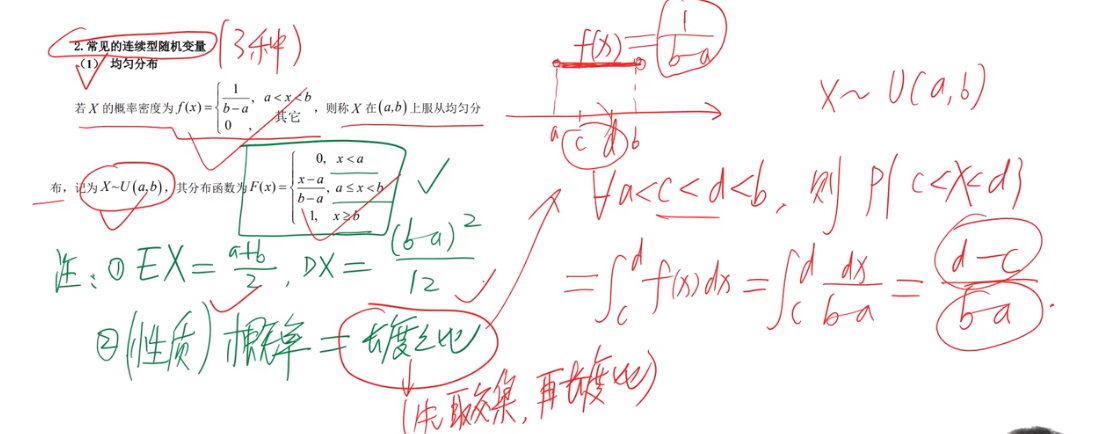
 常见的连续型随机变量分布：

 

指数分布

 

 

 

 注意：

 

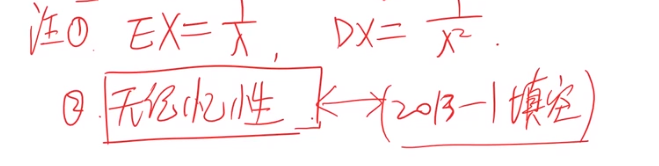
无记忆性

 

 

 

 

正态分布（核心）

 

 想要进阶最好还是都背过... 其实背过正态分布的概率密度 标准正态的那些也就带进去0 1 就行了

对称性和标准化常考：

 ps ： 不会真有人查看图片都不会看吧