神经网络与深度学习（三）：循环神经网络网络

给神经网络增加记忆能力

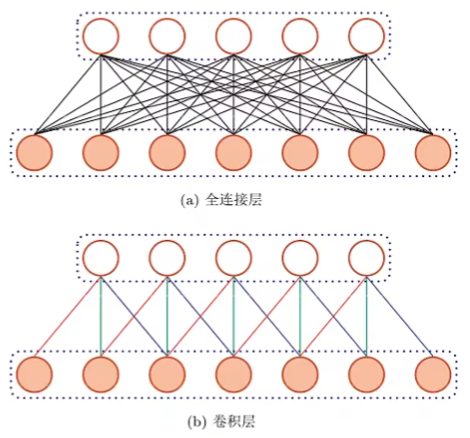
前馈神经网络：

  • 相邻两层之间存在单向连接，层内无连接
  • 有向无环图
  • 输入和输出的维数都是固定的，不能任意改变
  • （全连接前馈网络)无法处理变长的序列数据

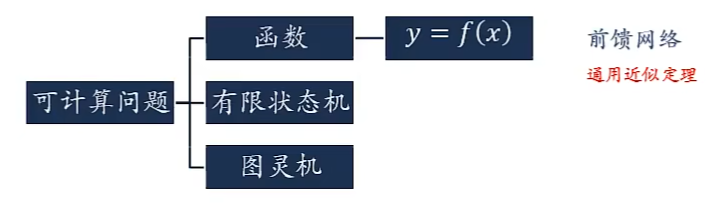
可计算问题：

image-20221108172055490

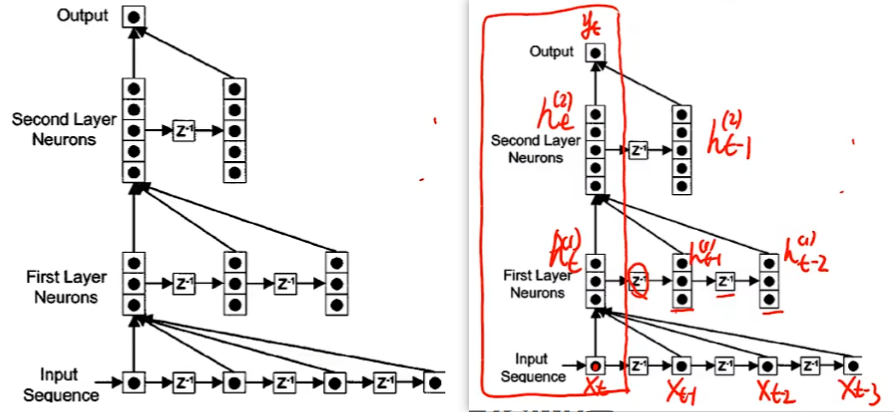
时延神经网络：

时延神经网络(Time Delay Neural Network,TDNN)

建立一个额外的延时单元，用来存储网络的历史信息（可以包括输入、输出、隐状态等)

\[\boldsymbol{h}_{t}^{(l)}=f\left(\boldsymbol{h}_{t}^{(l-1)}, \boldsymbol{h}_{t-1}^{(l-1)}, \cdots, \boldsymbol{h}_{t-K}^{(l-1)}\right) \]

这样，前馈网络就具有了短期记忆的能力。

image-20221108173940126

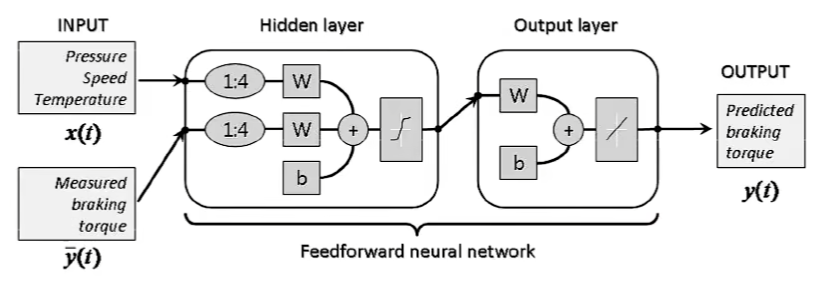
自回归模型（Autoregressive Model,AR）

一类时间序列模型，用变量y的历史信息来预测自己

\[\boldsymbol{y}_{t}=w_{0}+\sum_{k=1}^{K} w_{k} \boldsymbol{y}_{t-k}+\epsilon_{t} \]

\(\epsilon_{t} \sim N\left(0, \sigma^{2}\right)\)为第t个时刻的噪声

有外部输入的非线性自回归模型(Nonlinear Autoregressive with Exogenous Inputs Model,NARX)

\[\boldsymbol{y}_{t}=f\left(\boldsymbol{x}_{t}, \boldsymbol{x}_{t-1}, \cdots, \boldsymbol{x}_{t-K_{x}}, \boldsymbol{y}_{t-1}, \boldsymbol{y}_{t-2}, \cdots, \boldsymbol{y}_{t-K_{y}}\right) \]

其中f(·)表示非线性函数，可以是一个前馈网络.

\(K_x\)和\(K_y\)为超参数.

非线性自回归模型

image-20221108175122528

循环神经网络

循环神经网络通过使用带自反馈的神经元，能够处理任意长度的时序数据。

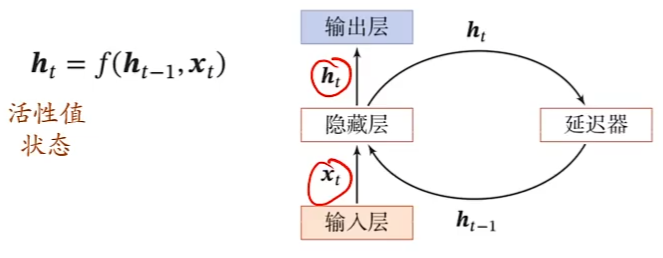
循环神经网络比前馈神经网络更加符合生物神经网络的结构。
循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。

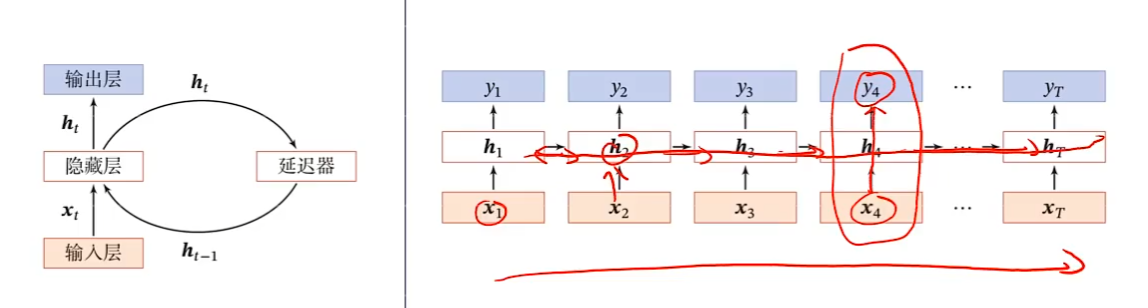
image-20221108180010743

图灵完备(Turing Completeness)是指一种数据操作规则，比如一种计算机编程语言，可以实现图灵机的所有功能，解决所有的可计算问题。

一个完全连接的循环神经网络可以近似解决所有的可计算问题。

作用

  • 输入-输出映射
    • 机器学习模型（本节主要关注这种情况）
  • 存储器
    • 联想记忆模型
  • 参考蒲公英书第8.6节

应用到机器学习

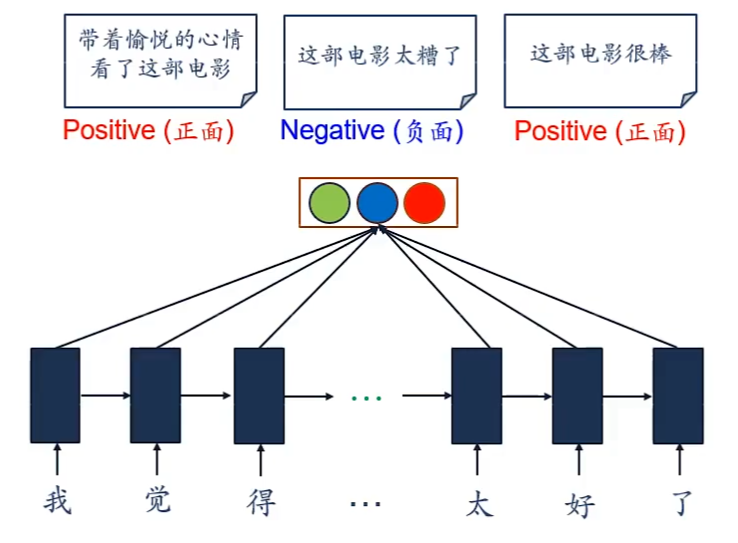
序列到类别

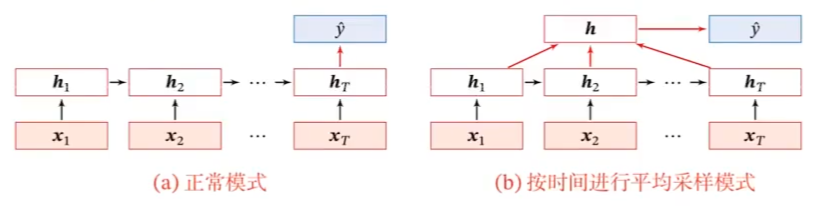
image-20221108180959201

真实情况：b

e.g.情感分类

image-20221108181442753

同步的序列到序列

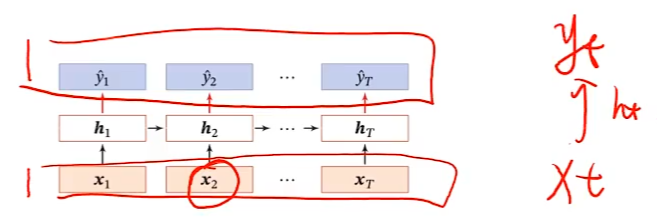
image-20221108181946026

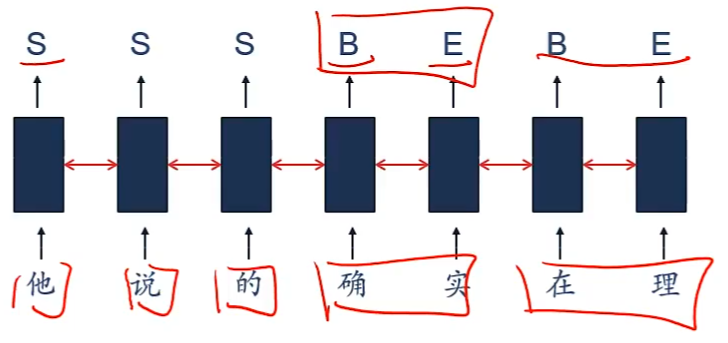
e.g.中文分词

image-20221108182056380

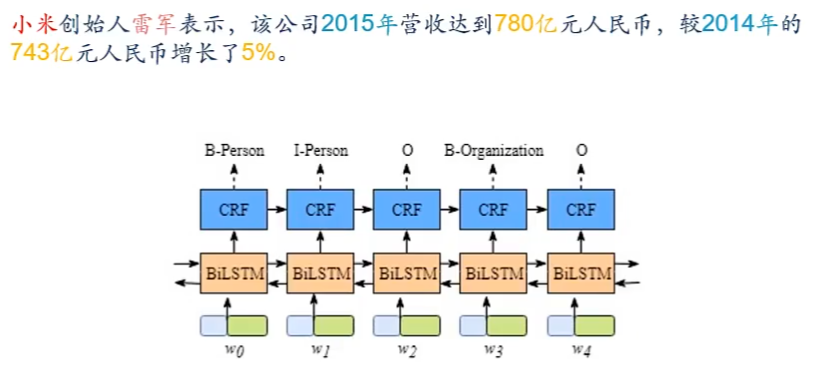
e.g.信息抽取

从无结构的文本中抽取结构化的信息，形成知识

image-20221108212720499

e.g.语音识别

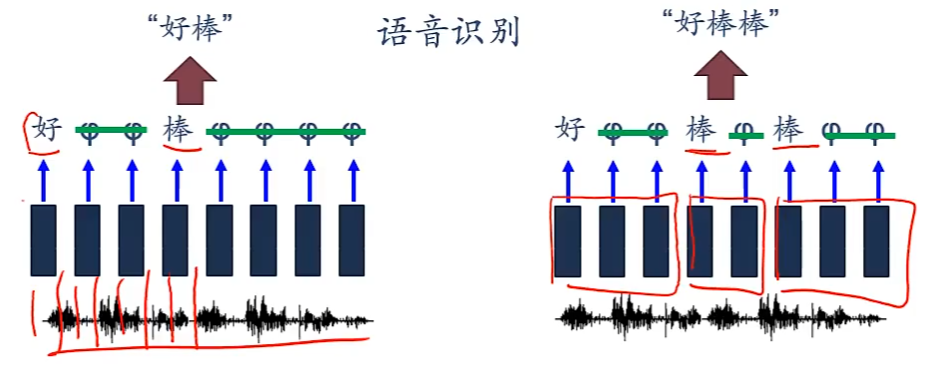
image-20221108213040367

异步的序列到序列

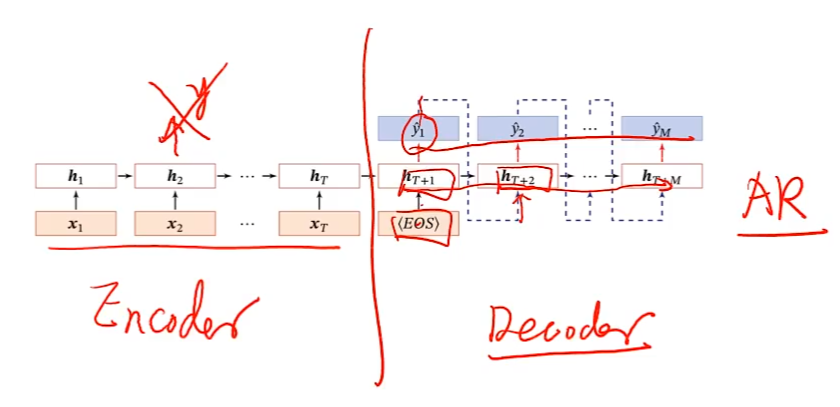
image-20221108213254199

e.g.机器翻译

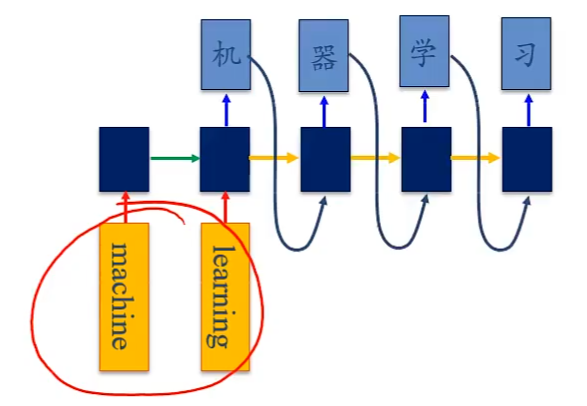
image-20221108213454708

参数学习与长程依赖问题

参数学习

机器学习

给定一个训练样本(x,y),其中
长度为T的输入序列\(\boldsymbol{x}=\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{T}\)
长度为T的标签序列\(\boldsymbol{y}=\boldsymbol{y}_{1}, \cdots, \boldsymbol{y}_{T}\)

时刻t的瞬时损失函数为

\[\mathcal{L}_{t}=\mathcal{L}\left(y_{t}, g\left(\boldsymbol{h}_{t}\right)\right) \]

总损失函数

\[\mathcal{L}=\sum_{t=1}^{T} \mathcal{L}_{t} \]

计算梯度

\[\begin{aligned} \boldsymbol{z}_{t} &=\boldsymbol{U} \boldsymbol{h}_{t-1}+\boldsymbol{W} \boldsymbol{x}_{t}+\boldsymbol{b} \\ \boldsymbol{h}_{t} &=f\left(\boldsymbol{z}_{t}\right) \end{aligned} \]

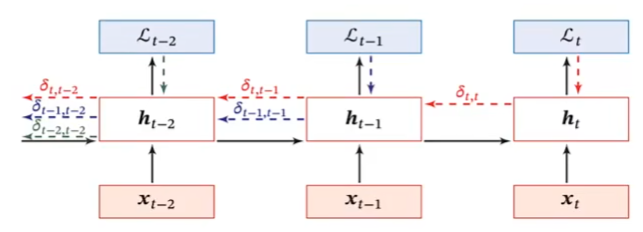image-20221108215431549 $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial \boldsymbol{U}} &=\sum_{t=1}^{T} \frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{U}} \\ \frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{U}} &=\sum_{k=1}^{t} \frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{z}_{k}} \boldsymbol{h}_{k-1}^{\top} \\ &=\sum_{k=1}^{t} \delta_{t, k} \boldsymbol{h}_{k-1}^{\top} \end{aligned} $$

\[\begin{aligned} \delta_{t, k} &=\frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{z}_{k}} \\ &=\frac{\partial \boldsymbol{h}_{k}}{\partial \boldsymbol{z}_{k}} \frac{\partial \boldsymbol{z}_{k+1}}{\partial \boldsymbol{h}_{k}} \frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{z}_{k+1}} \\ &=\operatorname{diag}\left(f^{\prime}\left(\boldsymbol{z}_{k}\right)\right) \boldsymbol{U}^{\top} \delta_{t, k+1} \end{aligned} \]

随时间反向传播算法(BackPropagation Through Time,BPTT)

\[\begin{aligned} \frac{\partial \mathcal{L}_{t}}{\partial \boldsymbol{U}} &=\sum_{k=1}^{t} \delta_{t, k} \boldsymbol{h}_{k-1}^{\top} \\ \delta_{t, k} &=\operatorname{diag}\left(f^{\prime}\left(\boldsymbol{z}_{k}\right)\right) \boldsymbol{U}^{\top} \delta_{t, k+1} \\ &=\prod_{\tau=k}^{t-1}\left(\operatorname{diag}\left(f^{\prime}\left(\boldsymbol{z}_{\tau}\right)\right) \boldsymbol{U}^{\top}\right) \delta_{t, t} \end{aligned} \]

长程依赖问题(Long-Term Dependencies Problem)

由于梯度爆炸或消失问题，实际上只能学习到短周期的依赖关系。

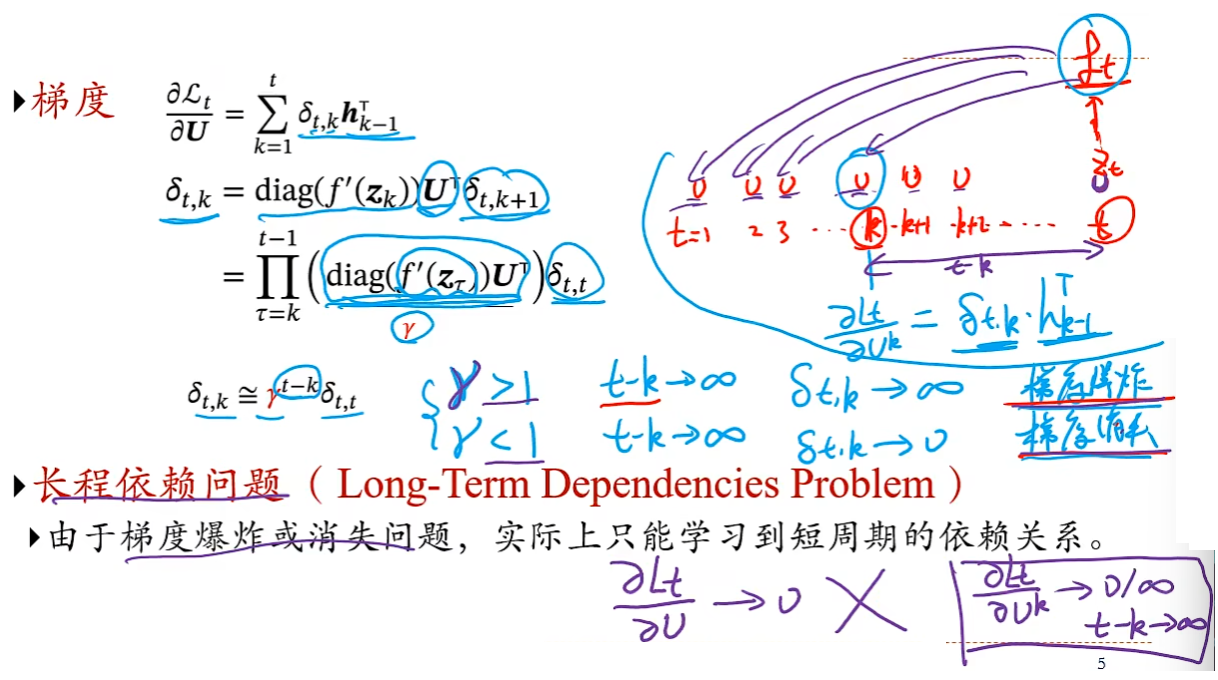
image-20221109091246038

如何解决长程依赖问题？

  • 循环神经网络在时间维度上非常深！
    • ​ 梯度消失或梯度爆炸
  • 如何改进？
    • ​ 梯度爆炸问题
      • ​ 权重衰减
      • ​ 梯度截断
    • 梯度消失问题
      • 改进模型
image-20221109100302438

残差网络？

门控机制

控制信息的累积速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息。

基于门控的循环神经网络(Gated RNN)

  • 门控循环单元GRU
  • 长短期记忆网络LSTM

GRU

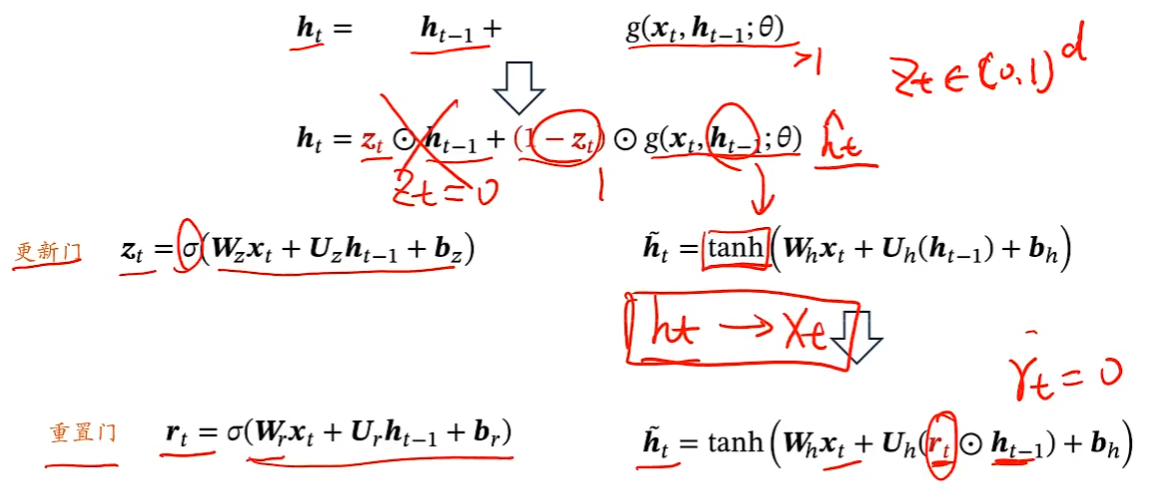
image-20221109101720914

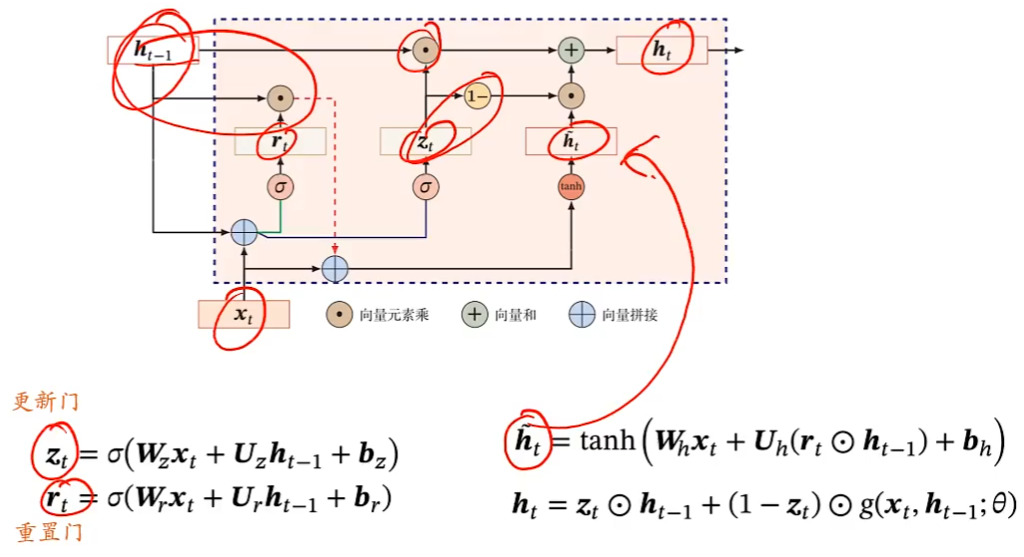
门控循环单元(Gated Recurrent Unit,GRU)

image-20221109102251090

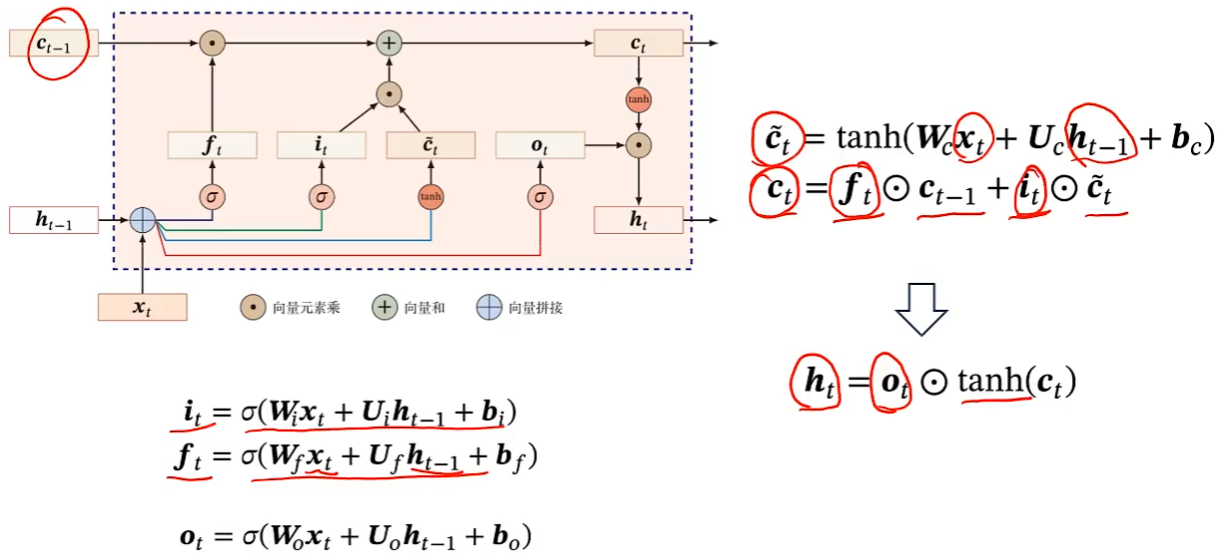
长短期记忆神经网络(Long Short-Term Memory,LSTM)

image-20221109102559113

LSTM的各种变体

image-20221109102738685

深层循环神经网络

堆叠循环神经网络（Stacked）

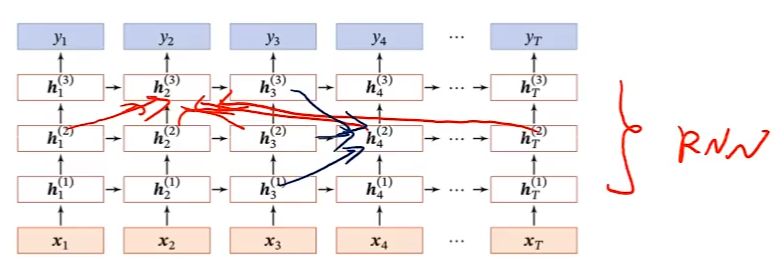
image-20221109103407969

双向循环神经网络

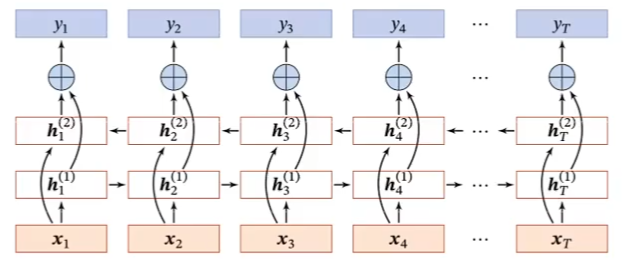
image-20221109103529477

循环神经网络小结

  • 优点：

    • 引入（短期)记忆

    • 图灵完备

  • 缺点：

    • 长程依赖问题

    • 记忆容量问题

    • 并行能力

循环网络应用

语言模型

自然语言理解：一个句子的可能性/合理性

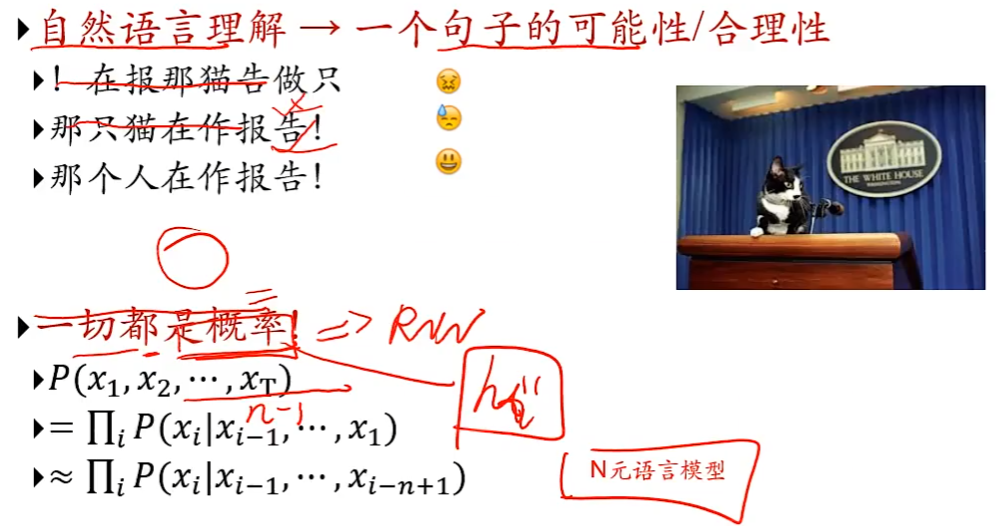
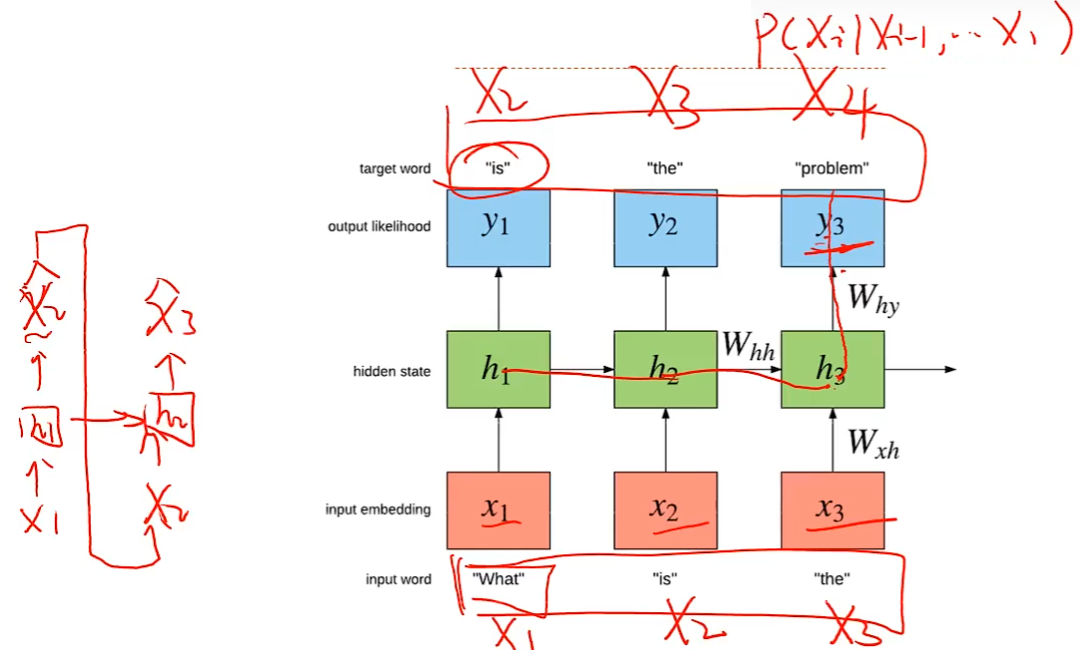
image-20221109104353819 image-20221109104556768

基于序列到序列的机器翻译:一个RNN用来编码,另一个RNN用来解码

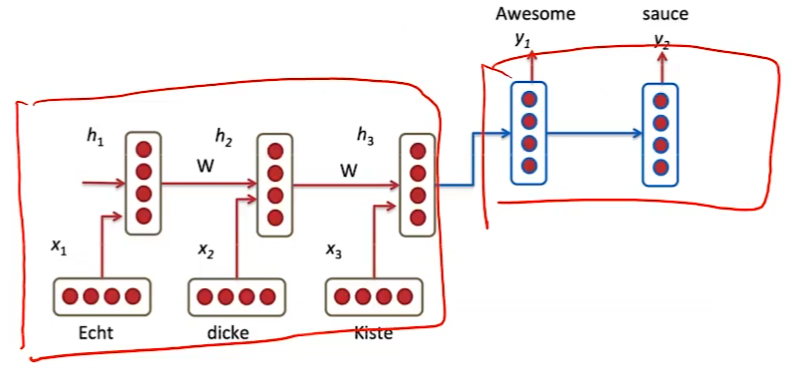
image-20221109105137411

写字、签名、对话系统...

扩展到图结构

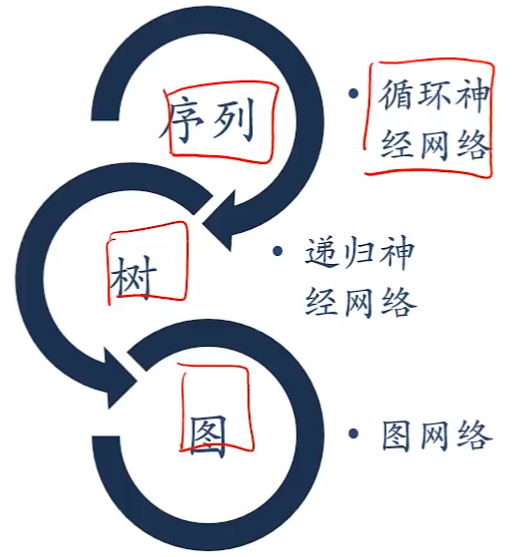
image-20221109105507262

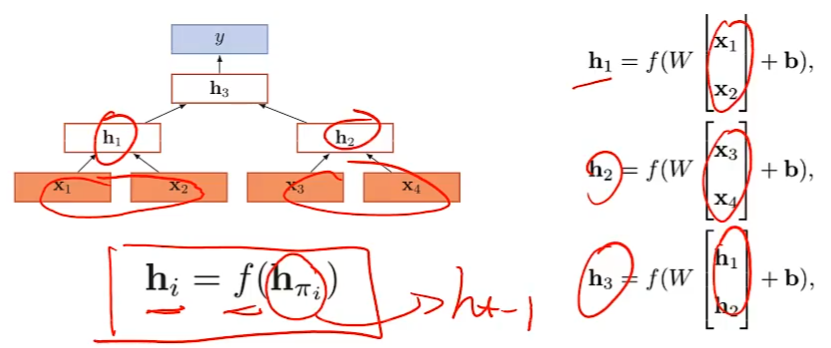
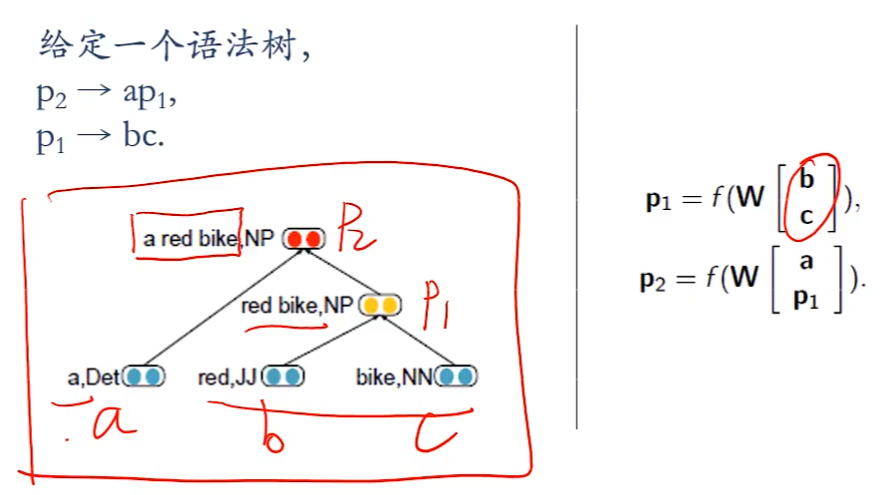
递归神经网络(Recursive Neural Network)

递归神经网络实在一个有向图无循环图上共享一个组合函数

image-20221109110030281

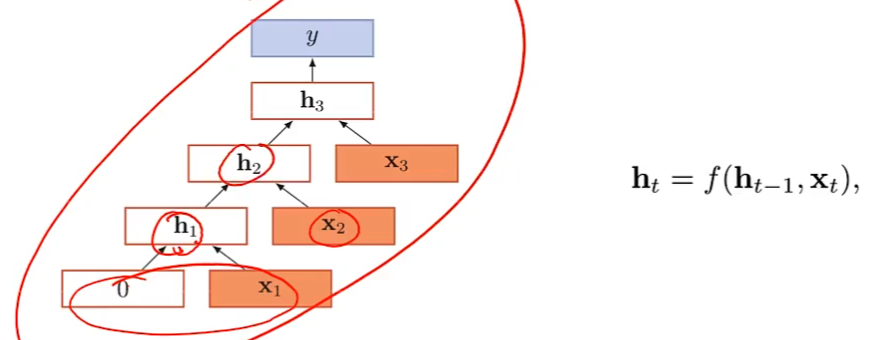
退化为循环神经网络

image-20221109110322373 image-20221109110403072

图数据

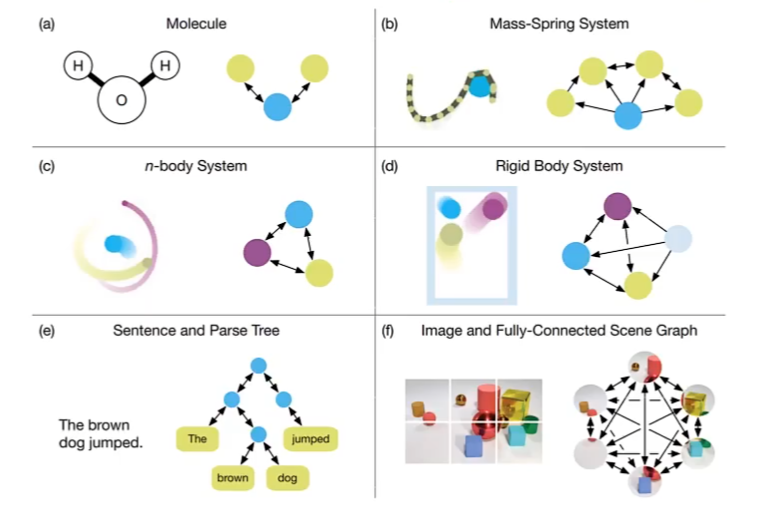
image-20221109111345657

图网络

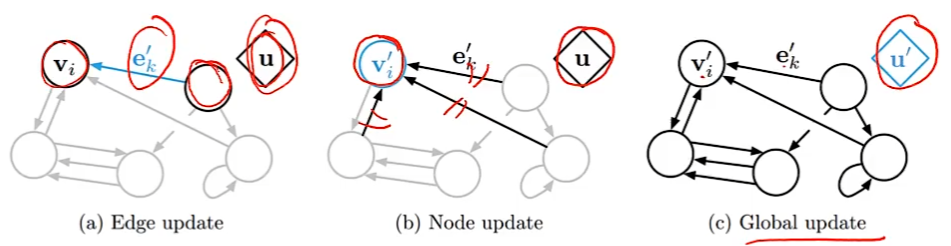
image-20221109111452923

对于一个任意的图结构G（V,E)

更新函数

\[\begin{aligned} \mathbf{m}_{t}^{(v)} &=\sum_{u \in N(v)} f\left(\mathbf{h}_{t-1}^{(v)}, \mathbf{h}_{t-1}^{(u)}, \mathbf{e}^{(u, v)}\right) \\ \mathbf{h}_{t}^{(v)} &=g\left(\mathbf{h}_{t-1}^{(v)}, \mathbf{m}_{t}^{(v)}\right) \end{aligned} \]

读出函数

\[\mathbf{y}_{t}=g\left(\left\{\mathbf{h}_{T}^{(v)} \mid v \in \mathcal{V}\right\}\right) \]

原创作者:孤飞-博客园
原文链接：https://www.cnblogs.com/ranxi169/p/16873036.html

posted @ 2022-11-09 11:24  孤飞  阅读(305)  评论(0)    收藏  举报