Atcoder Beginner Contest 257 problem F 题解

题目链接：点我

题目大意

有\(N\)个城镇，编号为\(1,2,……,N\)。

有\(M\)条路，第\(i\)条路连接城镇\(U_i\)和城镇\(V_i\)。每条路是双向的。一个人经过一条路从一边走到另一边需要\(1\)分钟。但对于某些道路，如果其\(U_i=0\)，则代表这条路的一边连接着\(V_i\)，但另一边不确定。

对于每一个\(i=1,2,……,N\)，回答以下问题：

如果所有的有不确定城镇的道路都连接到城镇\(i\)，那么一个人需要多少分钟才能从城镇\(1\)走到城镇\(N\)？输出这个时间。如果无法走到，则输出\(-1\)。

样例输入1

3 2
0 2
1 2

样例输出1

-1 -1 2

样例解释1

如果所有的未确定道路都连接到城镇\(1\)，则道路\(1\)和道路\(2\)都连接了城镇\(1\)和\(2\)。是不可能从城镇\(1\)走到城镇\(3\)的。

如果所有的未确定道路都连接到城镇\(2\)，则道路\(1\)连接了\(2\)号城镇自己，道路\(2\)连接了城镇\(1\)和\(2\)，也是不可能从城镇\(1\)走到城镇\(3\)的。

如果所有的未确定道路都连接到城镇\(3\)，则道路\(1\)连接了城镇\(2\)和\(3\)，道路\(2\)连接了城镇\(1\)和\(2\)，于是可以从用\(2\)分钟城镇\(1\)走到城镇\(3\)：

• 走道路\(2\)，用\(1\)分钟从城镇\(1\)走到城镇\(2\)。
• 走道路\(1\)，用\(1\)分钟从城镇\(2\)走到城镇\(3\)。

因此输出为 \(-1 \quad -1 \quad 2\)。

请注意，确定了不确定的道路连接到的城镇，可能有一条道路连接城镇和城镇本身，也可能有多条道路连接同一对城镇。

样例输入2

5 5
1 2
1 3
3 4
4 5
0 2

样例输出2

3 3 3 3 2

数据范围

• \(2 \leq N \leq 3 \times 10^5\)
• \(1 \leq M \leq 3 \times 10^5\)
• \(0 \leq U_i < V_i \leq N\)
• 如果\(i \neq j\)，则\((U_i,V_i) \neq (U_j,V_j)\)
• 所有的输入都为整型数。

---

解析

一道美丽的图论题。

构造一个图，并且构造一个城镇\(0\)。如果一条道路的一端连到了不确定的端点\(0\)，那么就直接连上城镇\(0\)。当我们确定这个不确定的城镇\(i\)时，那么就相当于在城镇\(0\)与城镇\(i\)之间连接了一条长度为\(0\)的虚拟边。

定义\(dis_{i,j}\)为城镇\(i\)道城镇\(j\)之间需要的时间。如果\(dis_{i,j}= +\infty\)，则代表\(i\)与\(j\)之间不能到达。

当回答第\(i\)个询问时，如果不需要经过城镇\(0\)就可以从城镇\(1\)走到城镇\(N\)的话，那么一个备选答案就是\(dis_{1,N}\)。

否则，需要经过城镇\(0\)的话，那么答案就为\(dis_{1,0}+dis_{i,N}\)或者是\(dis_{1,i}+dis_{n,0}\)。三者当中选最小值。

可以用下图作为参考。

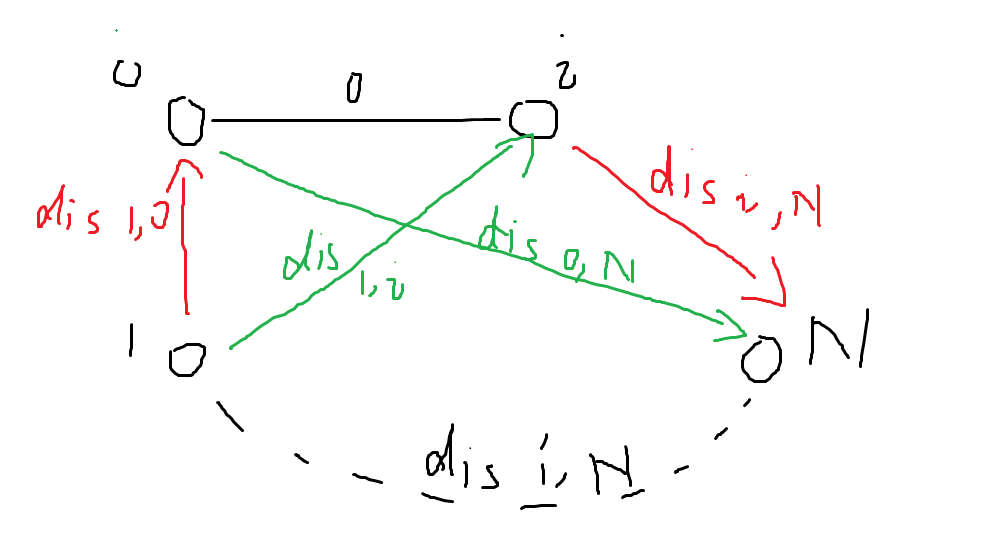
由于我们在实现过程中，只会用到以\(1\)和\(N\)为起点的\(dis\)值，因此我们可以跑两次bfs来计算出城镇\(1\)和\(N\)的\(dis\)值。

---

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5,INF=0x3f3f3f3f; //INF表示正无穷，即两边不可到达
int n,m;
int he[N],ne[N<<1],go[N<<1],val[N<<1],tot; //前向星
int vis[N],dis1[N],disn[N]; //vis为标记数组，dis1和disn分别表示从1和n开始的dis值
inline void add(int a,int b,int c){
	ne[++tot]=he[a];he[a]=tot;go[tot]=b;val[tot]=c;
} //加边
inline void bfs(int s,int *dis){
	memset(vis,0,sizeof vis);
	dis[s]=0; 
	queue<int>q;
	q.push(s);
	vis[s]=1;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=he[u];i;i=ne[i]){
			int v=go[i];
			if(!vis[v]){
				q.push(v);vis[v]=1;
				dis[v]=dis[u]+val[i]; //计算dis
			}
		}
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v,1);add(v,u,1);
	}
	memset(dis1,INF,sizeof dis1);
	memset(disn,INF,sizeof disn); //开始时全不可达
	bfs(1,dis1);
	bfs(n,disn); //bfs找到dis值
	for(int i=1;i<=n;i++){
		int ans=min(dis1[n],min(dis1[0]+disn[i],dis1[i]+disn[0])); //具体见图
		if(ans==INF) cout<<-1<<" "; //如果不可达
		else cout<<ans<<" ";
	}
	return 0;
}

完结撒花~