剑指 Offer 62. 圆圈中最后剩下的数字

目录

• 剑指 Offer 62. 圆圈中最后剩下的数字
  • 题目
  • 题解-链表
  • 题解-数学

剑指 Offer 62. 圆圈中最后剩下的数字

题目

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

限制：

1 <= n <= 10^5
1 <= m <= 10^6

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解-链表

这道题需要关注的是删除之后，在圈中的编号变了。后面应该往前移动，这里可以使用ArrayList不需要我们手动移动元素，我们还是通过索引来删除的元素。

这题不能用linkedList当成环形链表，因为链表靠索引找数字需要遍历会超时。

class Solution {
    public int lastRemaining(int n, int m) {
        ArrayList<Integer> list = new ArrayList();

        for(int i=0;i<n;i++){
            list.add(i);
        }
        int pos = 0;
        int tmp;
        while(n!=1){
            tmp = (pos+m-1)%list.size(); //使用取余来循环操作链表
            list.remove(tmp);
            pos = tmp;
            n--;
        }
        return list.get(0);
    }
}

这种暴力解法很容易超时。

题解-数学

只关心最终活着那个人的序号变化

每一轮删除了一个数字之后，又重新编号 下一个数字为0，重新找m个元素，所以我们需要在编号不断变化时找到原始的编号。

假设n个数字，删除第m个数字，最后安全的编号是f(n,m)

每一轮删除的元素 k = (m-1)%n
k+1 就是新一轮开头的0，我们需要找到新旧编号之间的联系

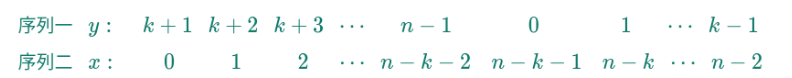
y代表原来的编号，代表新的编号
y-x = k+1 -> y = k+1+x
注意这里带入之后发现应该还要取余x与y都是大于0的，y = (k+1+x)%n

f(n,m)
= [k+1+f(n-1,m)]%n
= [(m-1)%n+1+f(n-1,m)]%n

最后一个肯定是0，那么我们用来倒推。

class Solution {
    public int lastRemaining(int n, int m) {
        int f = 0;
        for(int i=2;i<=n;i++){
            f= ((m-1)%i+1+f)%i;
        }
        return f;
    }
}

另一种推导思路
https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/tai-jiao-bi-ye-ye-neng-dong-dong-tai-gui-zmwj/