23.合并K个升序链表
23.合并K个升序链表
题目
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-k-sorted-lists
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解-两两合并
之前合并过2个链表,K个升序链表可以转换成 2个升序链表合并成一个有序链表
合并两个链表,参数是两个链表的头指针,返回合并后的头指针
ListNode merge2Lists(ListNode l1,ListNode l2){
ListNode dummy = new ListNode();//采用尾插法
ListNode tail = dummy; //记录结尾节点
ListNode tmp; //临时节点
while(l1 != null && l2 != null){
if(l1.val <= l2.val){
tmp = l1;
l1 = l1.next;
} else{
tmp = l2;
l2 = l2.next;
}
tail.next = tmp;
tail = tail.next; //指向末尾
}
//出循环说明有一个为空了,l1为空就连接上l2,否则就连接上l1
tail.next = l1==null?l2:l1;
return dummy.next;
}
//递归写法
ListNode merge2Lists(ListNode l1,ListNode l2){
if(l1==null) return l2;
if(l2==null) return l1;
if(l1.val<=l2.val){
l1.next = merge2Lists(l1.next , l2);
teturn l1;
}
l2.next = erge2Lists(l2.next , l1);
teturn l2;
}
接下来就是处理两两合并的问题了
int len = lists.length;
if(len == 0) return null;
ListNode tmp = lists[0];
for(int i=1;i<len;i++){
tmp = merge2Lists(tmp,lists[i]);
}
return tmp;
时间复杂度:O(NK) K为链表的长度,N为所有节点数
题解-归并合并
介绍
归并排序,当我们需要排序一个数组时,先将数组分成一半,然后想办法把左边的数组给排序,右边的数组给排序,之后再将它们归并起来。那现在对数组的排序就变成了对左边数组的排序和右边数组的排序。
当然了当我们对左边的数组和右边的素组进行排序的时候,再分别将左边的数组和右边的数组分成一半,然后对每一个部分先排序,再归并。如图:
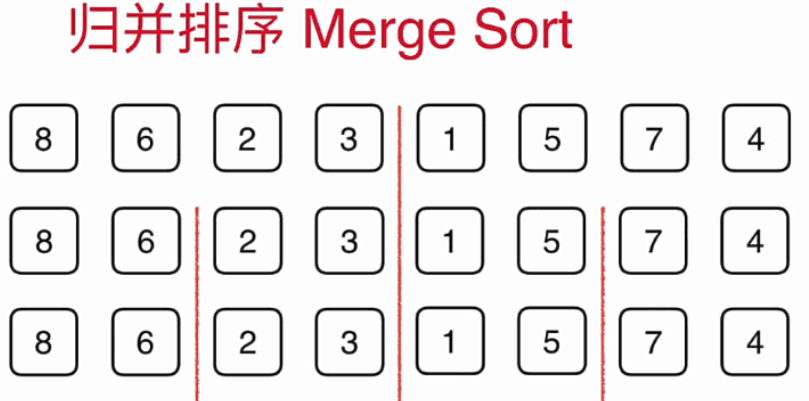
什么时候停止递归,只有一个元素时已经有序了,就不用再排序了,直接归并就好了。
这个思路不就是递归的思路吗!归并的过程就是在递归。
归并算法的实际复杂度 O(nlogn),递归的深度是logn 合并的的时间复杂度是n
题解
那么使用递归三部曲
递归的参数和返回值是什么
我们需要的是排好序合并之后的链表,那么返回值应该是排好序的数组元素ListNode。
需要将数组划分成一半,然后左边数组右边数组分别排序,那么参数首先需要有原始数组Lists,左指针left和右指针right来划分区间。
private ListNode merge(ListNode lists,int left,int right){}
递归终止条件
当数组里面只有一个元素时,就可以终止了,返回这个元素
if(right == left){
return lists[left];
}
本层递归逻辑
每层递归需要做什么事情?或者说本层递归需要做什么事情?
需要对左边已经排好序合并的链表和右边已经排好序合并的链表进行排序合并
mid = (left+right)/2
左边排好序合并的链表 merge(lists,left,mid)
右边排好序合并的链表 merge(lists,mid,right)
private ListNode merge(ListNode lists,int left,int right){
if(right == left) return lists[left];
int mid = (left+right)/2 ;//一分为二
ListNode l1 = merge(lists,left,mid);
ListNode l2 = merge(lists,mid+1,right);
return merge2Lists(l1,l2);
}
整体的代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
int len = lists.length;
if(len == 0) return null;
if(len == 1)return lists[0];
return merge(lists,0,len-1);
}
//归并排序
private ListNode merge(ListNode [] lists,int left,int right){
if(right == left) return lists[left];
int mid = (left+right)/2 ;//一分为二
ListNode l1 = merge(lists,left,mid);
ListNode l2 = merge(lists,mid+1,right);
return merge2Lists(l1,l2);
}
//合并两个
ListNode merge2Lists(ListNode l1,ListNode l2){
ListNode dummy = new ListNode();
ListNode tail = dummy;
ListNode tmp;
while(l1 != null && l2 != null){
if(l1.val <= l2.val){
tmp = l1;
l1 = l1.next;
} else{
tmp = l2;
l2 = l2.next;
}
tail.next = tmp;
tail = tail.next;
}
tail.next = l1==null?l2:l1;
return dummy.next;
}
}
K 条链表的总结点数是 N,平均每条链表有 N/K 个节点,因此合并两条链表的时间复杂度是 O(N/K)。归并算法的时间复杂度O(nlogn),因此 K 条链表会被合并 K * logK,因此总共的时间复杂度是 KlogKN/K 即 O(NlogK)。
归并算法的实际复杂度 O(nlogk) k是数组的长度,n是所有链表中元素的总和
题解-优先队列
实现优先队列的过程中进一步完成堆的其他操作
普通队列是“先进先出”
优先队列/优先级队列:每次出队列的元素都是优先级最高的元素
进行入队列的时候,就把元素插到数组末尾,然后进行向上调整
进行出队列的时候,删除堆顶元素,然后向下调整
优先队列内部的采用堆排序
利用小根堆的特点:父节点的值小于或等于子节点的值
把数据全部放进堆里,堆会根据节点的val自动排好序
父节点的值小于或等于子节点的值那么堆顶(根节点)一定是最小的值,我们把堆顶(根节点)输出之后,堆会重新排序产生新的堆顶(根节点)
使用优先队列,我们首先需要指明如何排序
//创建一个堆,并设置元素的排序方式
PriorityQueue<ListNode> queue = new PriorityQueue(
new Comparator<ListNode>() {
public int compare(ListNode o1, ListNode o2) {
return (o1.val - o2.val); //从小到大
}
});
//Lambad表达式
PriorityQueue<ListNode> queue = new PriorityQueue((o1,o2) -> o1.val-o2.val);
然后把链表的所有元素放进优先队里,依次取出队头元素
//遍历链表数组,然后将每个链表的每个节点都放入堆中
for(int i=0;i<lists.length;i++) {
while(lists[i] != null) {
queue.add(lists[i]);
lists[i] = lists[i].next;
}
}
//从链表中取出元素,采用尾插法
ListNode dummy = new ListNode(0);
ListNode tail = dummy;
while(!queue.isEmpty()){
tail.next = queue.poll();
tail = tail.next;
}
tail.next = null; //避免成环 ,因为进入队列的是节点,原来链表该节点后面是接着其他节点的
return dummy.next;
空间优化
这里我们是把所有的节点先全部放入优先队列中,那么每放入一个元素都会执行堆排序。
将原先的O(N)的空间复杂度优化到O(k) N是所有链表的节点总数,K是链表的条数。
最重要的是其实单个链表都是有序,我们可以利用这点,先比较开头位置的四个节点,找出最小的那他一定是最小的,然后再把他后面的节点放进去再找最小的节点。
先依次把所有链表的头节点放入堆
PriorityQueue<ListNode> queue = new PriorityQueue(
new Comparator<ListNode>() {
public int compare(ListNode o1, ListNode o2) {
return (o1.val - o2.val); //从小到大
}
});
int len = lists.length;
for(int i=0;i<len;i++){
ListNode tmp = lists[i];
if(tmp!=null)queue.add(tmp); //把每个链表的头节点放进去
}
然后从优先队列中取出队头元素,然后队头元素进队列
ListNode dummy = new ListNode(0);
ListNode tail = dummy;
while(queue.size()>0){
ListNode tmp = queue.poll();
tail.next = tmp;
tail =tail.next;
if(tmp.next!=null) queue.add(tmp.next);
}
tail.next = null; //与原来的状态断链
return dummy.next;
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
// PriorityQueue<ListNode> queue = new PriorityQueue(
// new Comparator<ListNode>() {
// public int compare(ListNode o1, ListNode o2) {
// return (o1.val - o2.val); //从小到大
// }
// });
//上述代码可以使用Lambda表达式
PriorityQueue<ListNode> queue = new PriorityQueue<>((o1,o2) -> o1.val - o2.val);
for(int i=0;i<lists.length;i++){
ListNode tmp = lists[i];
if(tmp!=null)queue.add(tmp); //把每个链表的头节点放进去
}
ListNode dummy = new ListNode(0);
ListNode tail = dummy;
while(queue.size()>0){
ListNode tmp = queue.poll();
tail.next = tmp;
tail =tail.next;
if(tmp.next!=null) queue.add(tmp.next);
}
tail.next = null; //与原来的状态断链
return dummy.next;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号