452.用最少数量的箭引爆气球

目录

• 452.用最少数量的箭引爆气球
  • 题目
  • 题解
    • 解法1
    • 解法2
    • 解法3

452.用最少数量的箭引爆气球

题目

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2

示例 4：

输入：points = [[1,2]]
输出：1

示例 5：

输入：points = [[2,3],[2,3]]
输出：1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

合并区间类的题目套路，采用贪心思想, 先排序, 然后遍历检查是否满足合并区间的条件

这里判断是否有交叉区间, 所以其实是计算已知区间的交集数量。

当气球的坐标有重叠部分的时候，就会被一箭射穿。有重叠部分的气球个数越多，需要的箭数越少。这里判断是否有交叉区间, 所以其实是计算已知区间的交集数量。

按照套路我们先排序，这道题有每个气球有两个维度，开始位置与结束位置，那我们选择哪个进行排序?

1.选择开始位置从小到大排序，可以看出，只要射击点的位置在交集区间内，那么都可以尽可能的射击多的气球。交集区间是随着气球的个数增加而变化的，交集区间的左右端点都不确定的，需要去维护交集区间。

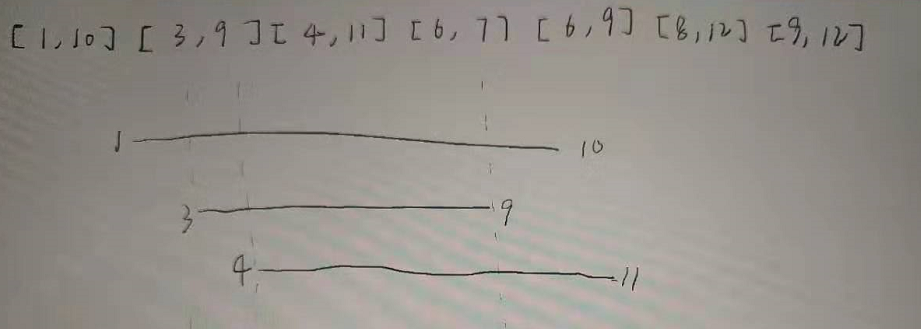
2.选择结束位置从小到大排序，可以看出，结束位置最小的在最前面，那么交集区间的右端点是确定的，只要气球的开始位置小于交集区间的右端点那么一定右重合部分。把射击点选在交际区间的右端点，就不需要去维护整个区间，只需要去维护端点就行了。

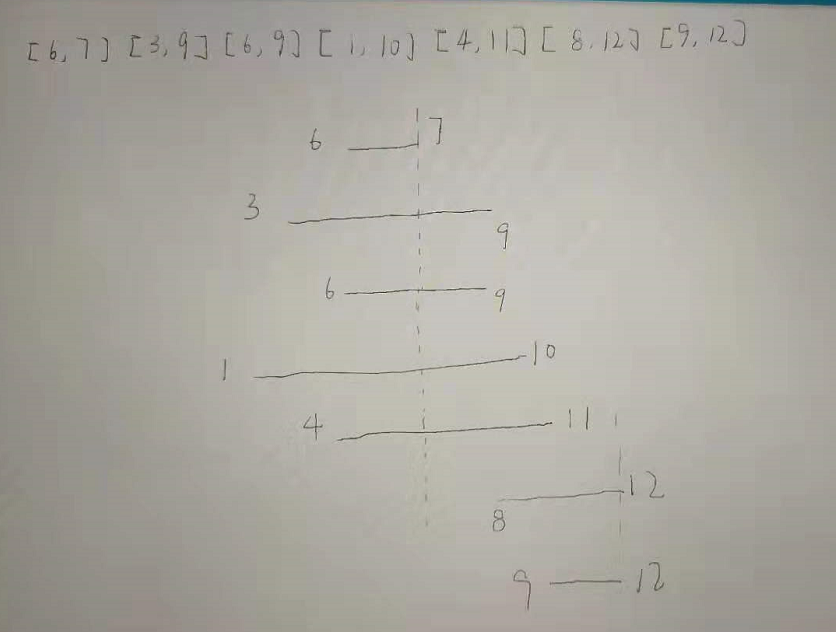
3.按照2的想法，那么是不是可以开始位置从大到小排序？这样交集区间的左端点是确定的。只要气球的结束位置大于左端点就行了。

下面分别对上述思路进行代码实现

解法1

1.选择开始位置从小到大排序，可以看出，只要射击点的位置在交集区间内，那么都可以尽可能的射击多的气球。交集区间是随着气球的个数增加而变化的，交集区间的左右端点都不确定的，需要去维护交集区间。

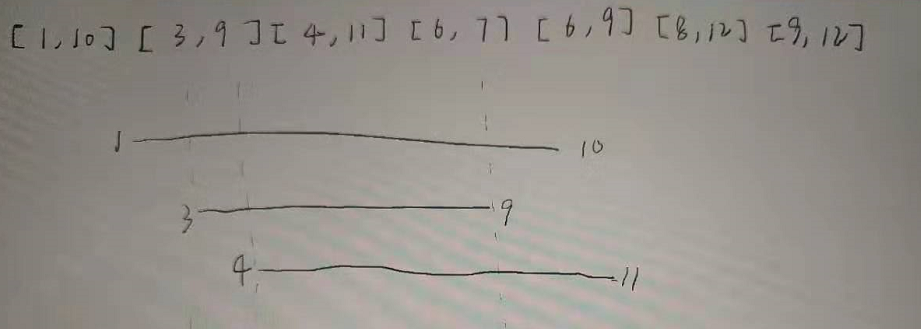
class Solution {
    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if(len==1) return 1;
        Arrays.sort(points,(o1, o2) -> Integer.compare(o1[0], o2[0])); 
        int count = 1;
        int [] range = new int []{points[0][0],points[0][1]}; //交集区间
        for(int i=1;i<len;i++){
            if(range[1]>=points[i][0]) //说明有交集，更新交集区间
            {
                    range[0] = points[i][0]; //排序之后后面的左端点肯定大于前面的
                    range[1] = Math.min(points[i][1],range[1]);
            }else{
                count++;
                range[0] = points[i][0];
                 range[1] = points[i][1];
            }

        }
        return count;
    }
}

注意

Arrays.sort(points,(o1, o2) -> o1[1]-o2[1]);

测试用例:[[-2147483646,-2147483645],[2147483646,2147483647]]
上面的排序就有问题了，这是因为差值过大而产生溢出。
sort的时候不要用a-b来比较，要用Integer.compare(a, b)!!!

解法2

选择结束位置从小到大排序，可以看出，结束位置最小的在最前面，那么交集区间的右端点是确定的，只要气球的开始位置小于交集区间的右端点那么一定右重合部分。把射击点选在交际区间的右端点，就不需要去维护整个区间，只需要去维护端点就行了。

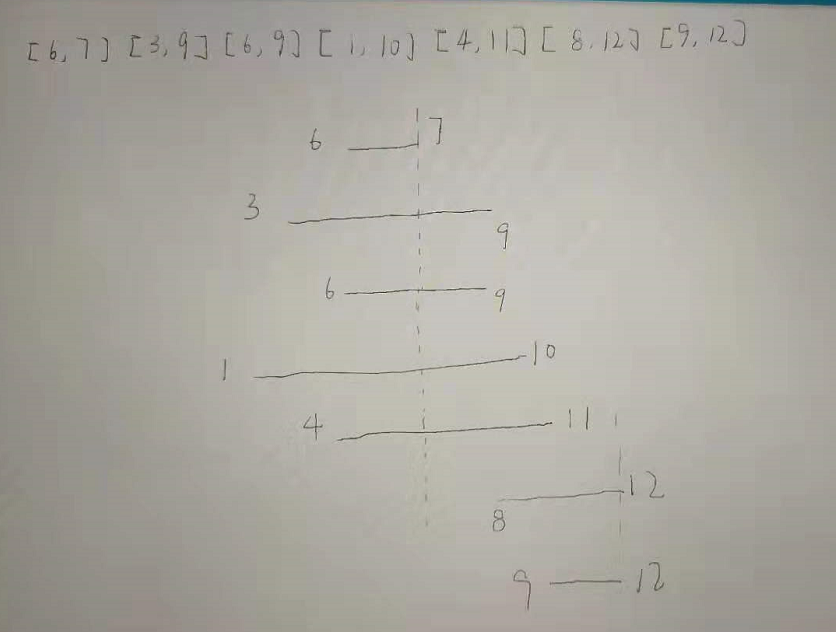
class Solution {
    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if(len==1) return 1;
        Arrays.sort(points,(o1, o2) -> Integer.compare(o1[1], o2[1])); 
        int count = 1;
        int point = points[0][1];
        for(int i=1;i<len;i++){
            if(point<points[i][0]) //没有重叠部分的气球就需要再用一个弓箭
            {
                    count++;
                    point=points[i][1];
            }
        }
        return count;
    }
}

解法3

解法3和解法2的思路其实是同一种，都是确定了交集区间的一个端点。

class Solution {
    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if(len==1) return 1;
        Arrays.sort(points,(o1, o2) -> Integer.compare(o2[0], o1[0])); 
        int count = 1;
        int point = points[0][0];
        for(int i=1;i<len;i++){
            if(point>points[i][1])
            {
                    count++;
                    point=points[i][0];
            }
        }
        return count;
    }
}