平面向量（1）

定义

顾名思义，平面向量是一个好东西

定义：向量：一个既有大小，又有方向的量。

注意：在平面向量中，一个向量可以任意平移，都是同一个向量，即向量可以平移。

有向线段的三要素：起点，方向，长度。

零向量：长度为 \(0\) 的向量，用 \(\vec{0}\) 表示。

单位向量：长度为一个单位的向量 \(\lvert \vec{a} \rvert =1\)。

相等向量：长度相等且方向相同的向量。

平行向量（共线向量）：方向相同或相反的非零向量。

注意：\(\vec{0}\) 平行于任意向量。

向量表示：

1. 几何表示（有向线段）
2. 小写字母（ \(\vec{a}\)）
3. 坐标 （ \(\vec{a}=(x,y)\)）

向量的线性运算

向量加法

向量加法有图中的三角运算： \(\vec{a}+\vec{b}\) 即将其首尾相接，从首连至尾的向量。

如图中 \(\vec{AB}+\vec{BC}=\vec{AC}\)

平行四边形运算，即三角运算但首相接，做平四，如图。

向量减法 和 向量数乘

注意：向量数乘是一个数 \(\lambda\) 乘上一个向量 \(\vec{a}\)。

向量减法是首重合，尾部相连，方向指向被减向量。

看图可知 \(\vec{a}=2\vec{b}\) 的意义（掌握）。

一些定理

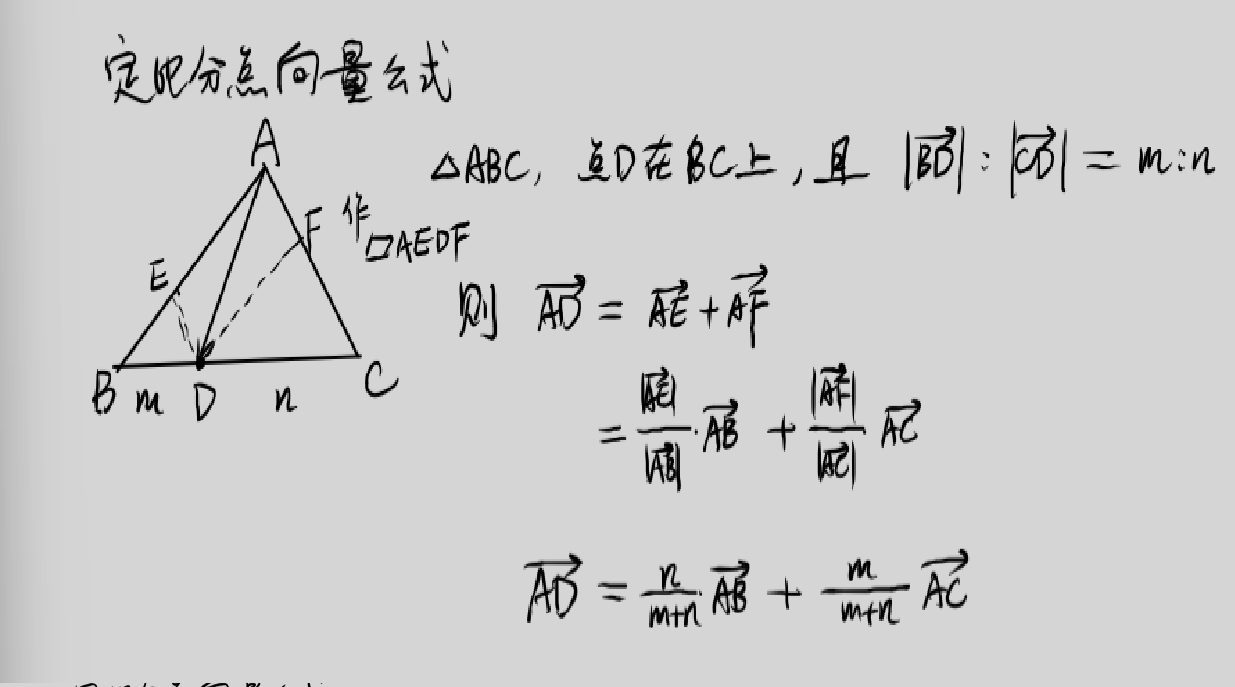
定比分点向量公式

重要程度：5⭐。

在一个三角形 \(ABC\) 中，\(D\) 是 \(BC\) 上一点，已知 \(\lvert \vec{BD} \rvert=m\)，\(\lvert \vec{DC} \rvert=n\)，可以用 \(\vec{AB}\) 和 \(\vec{AC}\) 来表示 \(\vec{AD}\)。

式子为： \(\vec{AD}=\vec{AB}\times \frac{n}{n+m}+\vec{AC}\times \frac{m}{n+m}\)。

十分有用，证明是做平行四边形，如图：

向量共线定理

\(\vec{a}(\vec{a}\neq \vec{0})与 \vec{b}共线\Leftrightarrow 唯一一个 \lambda ，使 \vec{b}=\lambda \vec{a}\)。

十分重要的推论：

\(A,B,C三点共线 \Leftrightarrow \vec{AB}，\vec{AC}共线\)；

重要：向量 \(\vec{PA},\vec{PB},\vec{PC}\) 三终点 \(A,B,C\) 三点共线 \(\Leftrightarrow\) 存在实数 \(\alpha ,\beta ,使得 \vec{PA}=\alpha \vec{PB} +\beta \vec{PC},且 \alpha +\beta =1\)。

浅浅证明了一下推论 \(2\)。

基底

不用讲啊，直接如图：

这张图是整个的图片，有一些例题可以在里面看，仅供参考：https://img2024.cnblogs.com/blog/3453453/202411/3453453-20241130215707507-2070136359.png 。