进制转换

一、二进制、八进制、十六进制转为十进制

对于一个N进制的数，整数部分从右往左第i位的位权为N^i-1，对于小数部分则要从左往右看，第j位的权值位N^-j。

例如将八进制12.36转换为十进制：

12.36=1*81+2*80+3*8-1+6*8-2=10.46875(十进制)

二、将十进制转换为二进制、八进制、十六进制

十进制转N进制时，小数部分和整数部分的操作方式不同：

1.整数部分采用"除N取余，逆序排列"的方法

• 将 N 作为除数，用十进制整数除以 N，可以得到一个商和余数；
• 之后用商继续除以N，保留每次得到的余数，直到商为0时停止；
• 逆序输出得到的余数，就能得到对应的

下图展示如何将十进制42转换为二进制数：

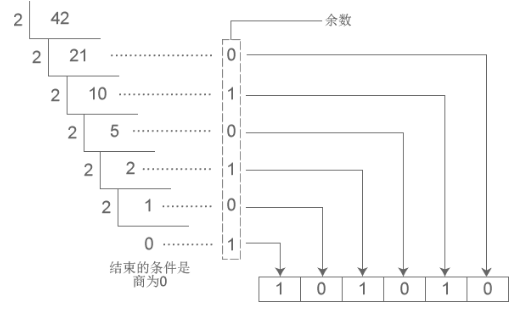
2.小数部分采用"乘N取整，顺序排列"的方法

• 用小数部分乘N，得到一个积，包含整数部分和小数部分；
• 取整数部分，然后用N再乘小数部分，保留每次得到的整数部分，直到小数为0或到达要求的精度
• 顺序排列得到的整数部分，得到小数对应的N进制数

下图展示如何将十进制小数0.6875转化为二进制小数的过程：

 注意，十进制小数转换成其他进制小数时，结果有可能是一个无限位的小数：

• 十进制 0.51 对应的二进制为 0.100000101000111101011100001010001111010111...，是一个循环小数；
• 十进制 0.72 对应的二进制为 0.1011100001010001111010111000010100011110...，是一个循环小数；
• 十进制 0.625 对应的二进制为 0.101，是一个有限小数。

三、二进制、八进制、十六进制之间的转换

这三种进制之间的转换可以采用更简单的方式

1.二进制和八进制之间的转换

一位八进制数可以使用三位的二进制数来表示，例如八进制的12，换算为二进制应该是001 002。

对于二进制转换为八进制也是同样的方法，每三位二进制数变为一位八进制数，高位不足就补0，例如二进制1011011，先化为001 011 011，对应的八进制位133。

2.二进制和十六进制之间的转换（和八进制类似）

一位十六进制数可以使用四位的二进制数来表示，例如十六进制的3C，换算为二进制应该是0011 1100。

对于二进制转换为十六进制每四位二进制数变为一位十六进制数，高位不足就补0，例如二进制1110110111，先化为0011 1011 0111，对应的十六进制数位3B8。

3.八进制和十六进制之间的转换可以使用二进制作为中间件进行转换