2020HDU多校第六场By Rynar 6827-6837

1005.Fragrant numbers

思路：区间dp，数据量只有5000，也可以打表

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
const int N=5000+20;
const int mod=998244353;
int dp[20][20][N];
int ans[N];
signed main(){
    string s="011451419191145141919";
    for (int i=1;i<13;i++){
        int tmp=0;
        for (int j=i;j<=15;j++){
            tmp=tmp*10+s[j]-'0';
            if (tmp>5000)break;
            dp[i][j][tmp]=1;
        }
    }
    for (int len=1;len<13;len++){//长度
        for (int i=1;i<13-len;i++){//左边界
            for (int j=i;j<i+len;j++){//中间点
                for (int l=1;l<=5000;l++){
                    if (!dp[i][j][l])continue;
                    for (int r=1;r<=5000;r++){
                        if (!dp[j+1][i+len][r])continue;
                        if (l+r<=5000)dp[i][i+len][l+r]=1;
                        if (l*r<=5000)dp[i][i+len][l*r]=1;
                    }
                }
            }
        }
    }
    for (int i=1;i<=13;i++){
        for (int j=1;j<=5000;j++){
            if (dp[1][i][j]&&!ans[j])ans[j]=i;
        }
    }
    int T,n;
    scanf("%d",&T);
    while (T--){
        scanf("%d",&n);
        printf("%d\n",ans[n]?ans[n]:-1);
    }
    return 0;
}

1007.A Very Easy Math Problem

思路：
莫比乌斯反演


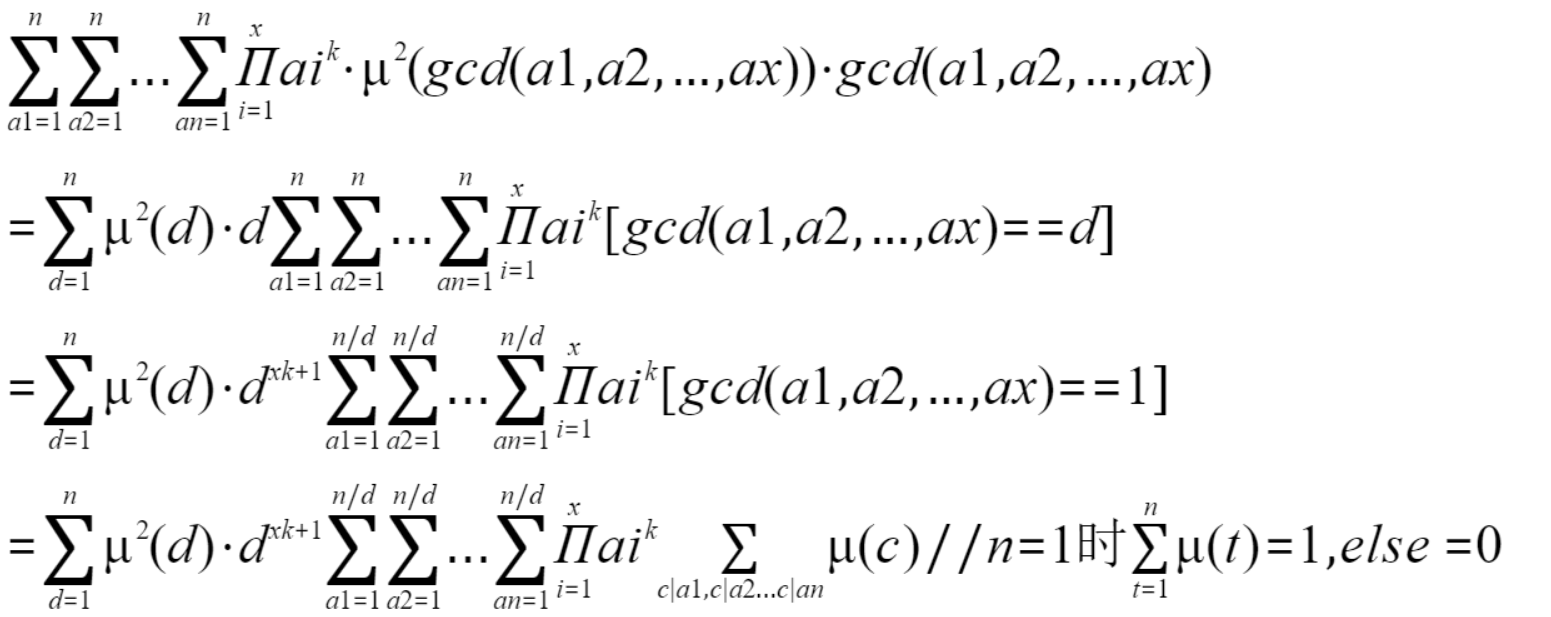
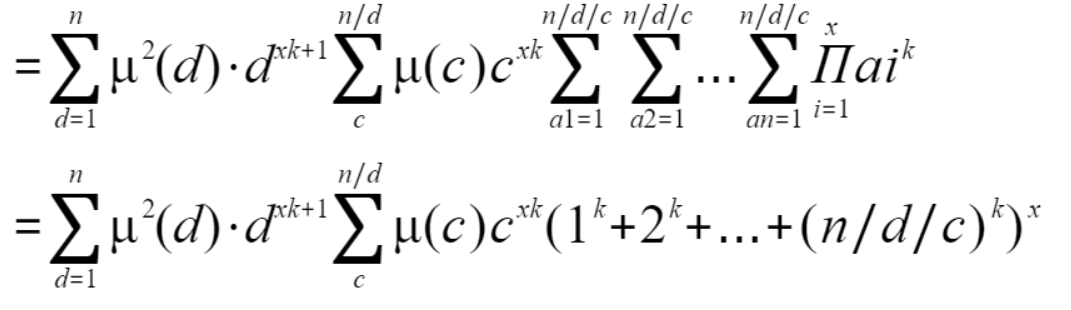
数论分块+数论分块 该做法O(nlogn+T*n^3/4)
也可继续化简 令T=cd

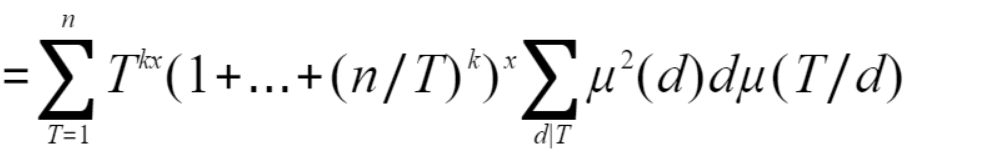
后面部分为积性函数，可由线性筛筛出
O(nlogn+Tn^1/2)

//O(nlogn+T*n\^3/4)
typedef long long ll;
const int N=2e5+10;
const int mod=1e9+7;
#define int ll
int n,m,k,x;
int dp[N];
int s[N],sc[N],sd[N];
int mu[N],vis[N],prim[N];
int qpow(int x,int y){
    int ans=1;
    while (y){
        if (y&1)ans=ans*x%mod;
        y>>=1;x=x*x%mod;
    }
    return ans;
}
void get_mu(int n){
    int cnt=0; 
    mu[1]=1;
    for(int i=2;i<=n;i++){
        if(!vis[i]){prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++){
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
}
int calc(int n){
    if(dp[n]!=-1)return dp[n];
    int ans=0;
    for(int l=1,r;l<=n;l=r+1){
        r=min(n,n/(n/l));
        (ans+=(sc[r]-sc[l-1])*s[n/l])%=mod;
    }
    return dp[n]=(ans+mod)%mod;
}
int calc2(int n){
    int ans=0;
    for(int l=1,r;l<=n;l=r+1){
        r=min(n,n/(n/l));
        (ans+=(sd[r]-sd[l-1])*calc(n/l))%=mod;
    }
    return (ans+mod)%mod;
}
signed main(){
    int T;
    memset(dp,-1,sizeof dp);
    scanf("%lld%lld%lld",&T,&k,&x);
    get_mu(N-1);
    for (int i=1;i<N;i++)(s[i]=s[i-1]+qpow(i,k))%=mod;
    for (int i=1;i<N;i++)s[i]=qpow(s[i],x);
    for (int i=1;i<N;i++)(sc[i]=sc[i-1]+mu[i]*qpow(i,k*x%(mod-1)))%=mod;
    for (int i=1;i<N;i++)(sd[i]=sd[i-1]+qpow(i,(x*k+1)%(mod-1))*mu[i]*mu[i])%=mod;
    while (T--){
        scanf("%lld",&n);
        printf("%lld\n",calc2(n));
    }
    return 0;
}

//O(nlogn+Tn\^1/2)
typedef long long ll;
const int N=2e5+10;
const int mod=1e9+7;
#define int ll
int n,m,k,x;
int f[N],s[N];
bitset<N>vis;
int prim[N];
int qpow(int x,int y){
    ll ans=1;
    while (y){
        if (y&1)ans=ans*x%mod;
        y>>=1;x=1ll*x*x%mod;
    }
    return ans;
}
void get_mu(int n){
    int cnt=0;
    f[1]=1;
    for(int i=2;i<=n;i++){
        if(!vis[i]){prim[++cnt]=i;f[i]=i-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++){
            vis[prim[j]*i]=1;
            if(i%prim[j]==0){
                if(i/prim[j]%prim[j]!=0){
                    f[i*prim[j]]=-prim[j]*f[i/prim[j]]%mod;
                }
                break;
            }
            else f[i*prim[j]]=f[i]*f[prim[j]]%mod;
        }
    }
    int sum=0;
    for (int i=1;i<N;i++){
        sum=(sum+qpow(i,k))%mod;
        s[i]=qpow(sum,x);
        f[i]=f[i]*qpow(i,k*x)%mod;
    }
    for (int i=1;i<N;i++){
        f[i]=(f[i]+f[i-1])%mod;
    }
}
signed main(){
    int T;
    scanf("%lld%lld%lld",&T,&k,&x);
    get_mu(N-1);
    while (T--){
        scanf("%lld",&n);
        int ans=0;
        for (int l=1,r;l<=n;l=r+1){
            r=n/(n/l);
            (ans+=(f[r]-f[l-1])*s[n/l]%mod)%=mod;
        }
        printf("%lld\n",(ans+mod)%mod);
    }
    return 0;
}

1010.Expectation

思路：把边拆成30个bit位，对每个bit位存在的边组成的图进行求图生成树个数*bit位的权值，再除以整个图的生成树个数

typedef long long ll;
const int N=100+10;
const int mod=998244353;
#define int ll
int n,m;
int K[N][N];
int x[N*N],y[N*N],z[N*N];
int gauss(int n){//高斯消元求图的生成树个数
    int res=1;
    for(int i=1;i<=n-1;i++){//枚举主对角线上第i个元素
        for(int j=i+1;j<=n-1;j++){//枚举剩下的行
            while(K[j][i]){//辗转相除
                int t=K[i][i]/K[j][i];
                for(int k=i;k<=n-1;k++)//转为倒三角
                    K[i][k]=(K[i][k]-t*K[j][k]+mod)%mod;
                swap(K[i],K[j]);//交换i、j两行
                res=-res;//取负
            }
        }
        res=(res*K[i][i])%mod;
    }
    return (res+mod)%mod;
}
int build(int p){
    for (int i=1;i<=n;i++){
        for (int j=1;j<=n;j++){
            K[i][j]=0;
        }
    }
    for (int i=1;i<=m;i++){//度数矩阵-边矩阵
        if (z[i]&p){
            K[x[i]][x[i]]++;
            K[y[i]][y[i]]++;
            K[x[i]][y[i]]--;
            K[y[i]][x[i]]--;
        }
    }
    return gauss(n)*p%mod;
}
int bu(){
    for (int i=1;i<=n;i++){
        for (int j=1;j<=n;j++){
            K[i][j]=0;
        }
    }
    for (int i=1;i<=m;i++){
        K[x[i]][x[i]]++;
        K[y[i]][y[i]]++;
        K[x[i]][y[i]]--;
        K[y[i]][x[i]]--;
    }
    return gauss(n);
}
int qpow(int x,int y){
    int ans=1;
    while (y){
        if (y&1)ans=ans*x%mod;
        y>>=1;x=x*x%mod;
    }
    return ans;
}
signed main(){
    int T;
    scanf("%lld",&T);
    while (T--){
        scanf("%lld%lld",&n,&m);
        for (int i=1;i<=m;i++){
            scanf("%lld%lld%lld",&x[i],&y[i],&z[i]);
        }
        int ans=0;
        for (int i=0;i<=29;i++){
            ans=(ans+build(1<<i))%mod;
        }
        ans=ans*qpow(bu(),mod-2)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}