2020HDU多校第一场By Rynar 6751-6762

1001.Avian Darts

1002.Boring Task

1003.Cookies

1004.Distinct Sub-palindromes

签到题

int n,m,k;
void solve(){
    cin>>n;
    if (n==1)cout<<26<<endl;
    else if (n==2)cout<<676<<endl;
    else if (n==3)cout<<17576<<endl;
    else cout<<24*25*26<<endl;
}
int main(){
    int T;
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

1005.Fibonacci Sum

题意：斐波那契数列，T<=200,读入N<=1e18,C<=1e18,K<=1e5,求F(0)^K+F(C)^K+F(2C)^K+...+F(NC)^K,mod=1e9+9
思路：先利用二次剩余的模板求出sqrt(5)%mod的值,处理出a=(1+sqrt(5))/2,b=(1-sqrt(5))/2的模值

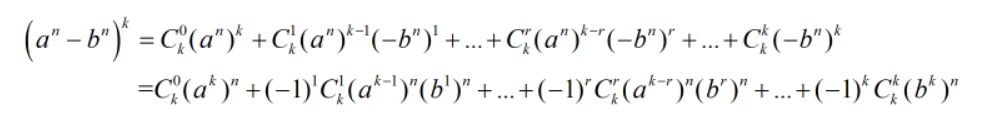
利用0,c,2c...nc等比公式算出每项公式

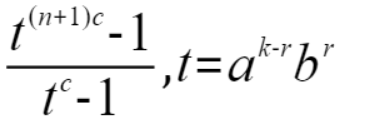
n为nc，r是变化量
构造t的上下的递推式进行累加

const int C=276601605;//1/sqrt(5)
const int A=691504013;//(1+sqrt(5))/2
const int AA=691504012;//A^-1
const int B=308495997;//(1-sqrt(5))/2
const int N=5e5+10;
const int mod=1e9+9;
int f[N],g[N],inv[N];
void init() {
    f[0]=g[0]=inv[0]=f[1]=g[1]=inv[1]=1;
    for (int i=2;i<N;i++){
        f[i]=(ll)f[i-1]*i%mod;//阶乘
        inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;//逆元
        g[i]=(ll)g[i-1]*inv[i]%mod;//阶乘的逆元
    }
}
inline int qpow(ll x,ll y){
    ll ans=1;
    while (y){
        if (y&1)ans=ans*x%mod;
        y>>=1;x=x*x%mod;
    }
    return ans;
}
inline int nCm(int n,int m){
    if (m<0||m>n)return 0;
    return (ll)f[n]*g[m]%mod*g[n-m]%mod;
}
inline void add(int &u,int v){
    u+=v;
    if (u>=mod)u-=mod;
}
void solve(){
    ll n,c;
    int k;
    scanf("%lld%lld%d",&n,&c,&k);
    int DD=(ll)qpow((ll)AA*B%mod,c)%mod;//(B/A)^c
    int q=qpow(qpow(A,c),k);//A^(ck)
    int n1=(n+1)%mod;
    int n2=(n+1)%(mod-1);//欧拉降幂
    int Q=qpow(q,n2);//A^(ck(n+1))
    int D=qpow(DD,n2);//(B/A)^(c(n+1))
    int ans=0;
    for (int i=0;i<=k;i++){
        int t=nCm(k,i);
        if (i&1)t=mod-t;
        if (q==1)add(ans,(ll)t*n1%mod);//不能直接/q-1,直接*(n+1)
        else add(ans,(ll)t*(Q+mod-1)%mod*qpow(q-1,mod-2)%mod);
        q=(ll)q*DD%mod;//A^(ck)->A^c(k-1)*B^c->...->B^(ck)
        Q=(ll)Q*D%mod;//A^(ck(n+1))->A^(c(k-1)(n+1))*B^(c(n+1))->...->B^(ck(n+1))
    }
    printf("%lld\n",(ll)ans*qpow(C,k)%mod);
}
int main(){
    int T;
    init();
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

1006.Finding a MEX

1007.Hunting Monsters

1008.Integral Calculus

1009.Leading Robots

题意：已知n个人的起始位置和加速度，问有多少个人可能过达到第一名，并列第一不算
思路：先按照位置排序，位置相同按加速度排序，去除位置和加速度相同的保留一个并用map记录，去除位置较后但是加速度较慢的，再利用s1+a1*t1^2=s2+a2*t1^2与s1+a1*t2^2=s3+a3*t2^2 比较t1和t2,用栈，每次新一个位置和加速度，都和前两个进行比较t1和t2,若后一个人会比前一个人较早赶上前前一个人，则去除前一个人，i--继续往前和前两个人比较

const int N=5e5+10;
int n,m,k;
struct node{
    ll s,a;
}b[N],c[N];
bool cmp(node a,node b){
    if (a.s==b.s)return a.a>b.a;
    return a.s>b.s;
}
stack<pair<ll,ll> >q;
ll a[N],s[N];
map<pair<ll,ll>,bool>mp;
void solve(){
    int x,y,z;
    mp.clear();
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%lld%lld",&b[i].s,&b[i].a);
    sort(b+1,b+1+n,cmp);
    int cnt=0;
    ll p1=b[1].a,p2=b[1].s,ss=1;
    for (int i=2;i<=n;i++){
        if (b[i].a==p1&&b[i].s==p2)ss++;
        else{
            if (ss==1){
                c[++cnt].a=p1,c[cnt].s=p2;
                p1=b[i].a,p2=b[i].s;
            }
            else{
                c[++cnt].a=p1,c[cnt].s=p2;
                mp[{p1,p2}]=1;
                p1=b[i].a,p2=b[i].s;
                ss=1;
            }
        }
    }
    if (ss==1)c[++cnt].a=p1,c[cnt].s=p2;
    else{
        c[++cnt].a=p1,c[cnt].s=p2;
        mp[{p1,p2}]=1;
    }
    for (int i=1;i<=cnt;i++)b[i]=c[i];
    ll g=b[1].a;
    n=cnt;
    cnt=1;
    a[cnt]=b[1].a,s[cnt]=b[1].s;
    for (int i=2;i<=n;i++){
        if (b[i].a>g){
            a[++cnt]=b[i].a,s[cnt]=b[i].s;
            g=b[i].a;
        }
    }
    n=cnt;
    if (n)q.push({a[1],s[1]});
    if (n>1)q.push({a[2],s[2]});
    for (int i=3;i<=n;i++){
        if (q.size()<2){
            q.push({a[i],s[i]});
            continue;
        }
        ll a1,a2,s1,s2,a3,s3;
        a2=q.top().first,s2=q.top().second;
        q.pop();
        a1=q.top().first,s1=q.top().second;
        a3=a[i],s3=s[i];
        if ((s1-s2)*(a3-a1)>=(a2-a1)*(s1-s3))i--;
        else q.push({a2,s2}),q.push({a3,s3});
    }
    int t=q.size();
    while (!q.empty()){
        if (mp[{q.top().first,q.top().second}])t--;
        q.pop();
    }
    printf("%d\n",t);
}
int main(){
    int T=1;
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

1010.Math is Simple

1011.Minimum Index

题意：给定一个字符串s(sum of s<=2e7),求1-n的前缀每个前缀的最小字典序后缀的位置k*1112^(i-1)，例k=1时,contest的后缀为contest
思路：SAM会被卡，要使用lyndon分解。

const int N=1e6+10;
const int mod=1e9+7;
char s[N];
int p[N];//记录每个点的所属lyndon串的左端点
int main(){
    int T;
    cin>>T;
    while (T--){
        scanf("%s",s+1);
        int n=strlen(s+1);
        for (int i=1;i<=n;i++)p[i]=0;
        int i=1,j,k;
        while (i<=n){
            p[i]=i;
            for (j=i,k=i+1;k<=n&&s[k]>=s[j];k++){
                if (s[k]>s[j])j=i,p[k]=i;
                else p[k]=p[j]+k-j,j++;
            }
            while(i<=j)i+=k-j;
        }
        ll t=1,ans=0;
        for (int i=1;i<=n;i++){
            ans=(ans+t*p[i]%mod)%mod;
            t=t*1112%mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

1012.Mow