2020牛客多校第三场By Rynar

A.Clam and Fish

思路：贪心，没啥好说

int n,m,k;
string s;
void solve(){
    cin>>n;
    cin>>s;
    int f=0,c=0;
    for (int i=0;i<n;i++){
        if (s[i]=='0'){
            if (c)c--,f++;
        }
        else if (s[i]=='1')c++;
        else f++;
    }
    f+=c/2;
    cout<<f<<endl;
}
int main(){
    int T=1;
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

B.Classical String Problem

思路：记录头指针

int n,m,k,p;
string s;
void solve(){
    char c;
    int x;
    getchar();
    scanf("%c %d",&c,&x);
    if (c=='M'){
        p=(p+x+k)%k;
    }
    else{
        printf("%c\n",s[(p+x-1)%k]);
    }
}
int main(){
    int T=1;
    cin>>s;
    k=s.size();
    p=0;
    cin>>T;
    while (T--){
    	solve();
    }
    return 0;
}

C.Operation Love

题意：

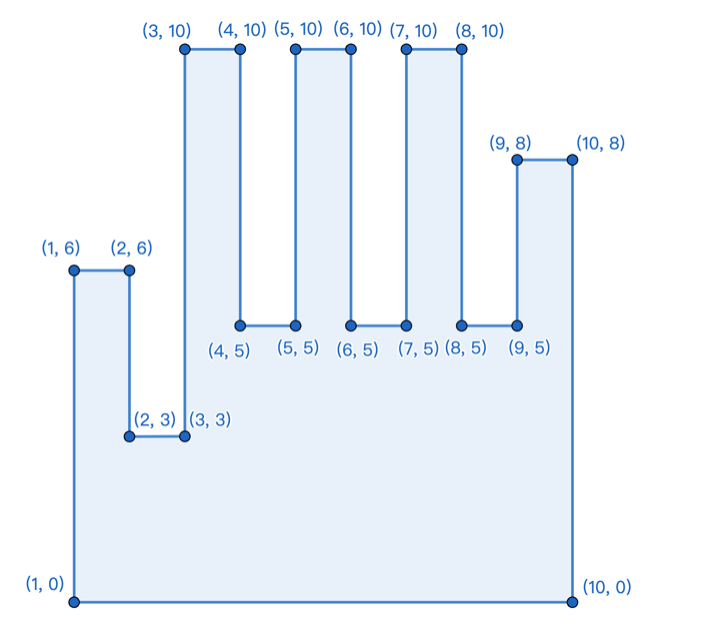
将这只任意翻转旋转过的手的20个坐标顺时针或逆时针给你，问是左手还是右手
思路：先用叉积判断出给出顺逆时针，再通过边长的关系得出左手还是右手

#define sqr(a) (a)*(a)
const double eps=0.1;
string s;
double x[21],y[21];
void solve(){
    for (int i=0;i<20;i++)scanf("%lf%lf",&x[i],&y[i]);
    double ans=0;
    for (int i=0;i<20;i++)ans+=x[i]*y[(i+1)%20]-x[(i+1)%20]*y[i];//鞋带公式 
    ans/=2;//面积,<0顺时针,>0逆时针
    int a,b;
    for (int i=0;i<20;i++){
        double t=sqrt(sqr(x[i]-x[(i+1)%20])+sqr(y[i]-y[(i+1)%20])); 
        if (t<=9+eps&&t>=9-eps)a=i;
        if (t<=8+eps&&t>=8-eps)b=i;
    }
    if ((a<b&&!(a==0&&b==19))||(a==19&&b==0)){
        if (ans>0) puts("right");
        else puts("left");
    }
    else{
        if (ans>0) puts("left");
        else puts("right");
    }
}
int main(){
    int T=1;
    cin>>T;
    while (T--){
    	solve();
    }
    return 0;
}

D.Points Construction Problem

题意：给定n,m,n代表n个黑点,m代表黑点和周围空白区域构成的黑白点对个数，问满足n和m图形能否构成
思路：分析得,一个凸的黑点构成的图形形成的点对为其外长方形的周长，也易知,m为奇数，该图形无法构成。
不妨令所有点外围为同一个长方形
最少点构成最大图形

最多点构成图形为长方形整体
中间部分的点可以如图补充，左边同右边

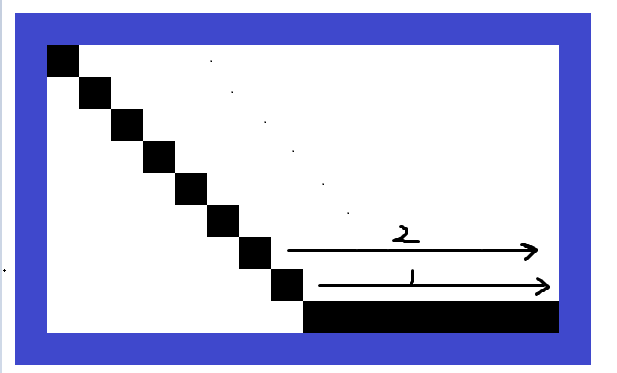
可以枚举1-m/2,长宽为a,b,当点在max(a,b)<=n<=a*b时满足

int n,m,k;
void solve(){
    cin>>n>>m;
    if (m&1){cout<<"No"<<endl;return;}
    bool f=0;
    int a,b;
    for (int i=1;i<=m/2/2;i++){//枚举长宽的宽 
        a=i,b=m/2-i;
        if (n>=b&&n<=a*b){f=1;break;}
    }
    if (f==0){cout<<"No"<<endl;return;}
    cout<<"Yes"<<endl;
    n-=b;
    for (int i=1;i<=a;i++)printf("%d %d\n",i,i);
    for (int i=a+1;i<=b;i++)printf("%d %d\n",a,i);
    for (int i=a-1;i>=1;i--){
        if (n==0)break;
        for (int j=i+1;j<=b;j++){
            printf("%d %d\n",i,j);
            n--;
            if (n==0)break;
        }
    }
    for (int i=2;i<=a;i++){
        if (n==0)break;
        for (int j=i-1;j>=1;j--){
            printf("%d %d\n",i,j);
            n--;
            if (n==0)break;
        }
    }
}
int main(){
    int T=1;
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

E.Two Matchings

题意：原序列为a,长度为n,n为偶数,寻找两个置换序列p,q,满足a[p[i]]!=i,a[p[p[i]]]=i,问的最小值
思路：只要满足4个点及以上一组就必定能形成2个置换序列,值为组中的(max-min)*2,先排序,再利用动态规划即可求出最小值

int n,m,k;
int a[N],dp[N];
void solve(){
    cin>>n;
    for (int i=1;i<=n;i++)scanf("%d",&a[i]);
    sort(a+1,a+1+n);
    for (int i=1;i<=n;i++)dp[i]=inf;
    dp[0]=0;
    for (int i=4;i<=n;i++){
        dp[i]=min(dp[i],dp[i-4]+a[i]-a[i-3]);
        dp[i]=min(dp[i],dp[i-2]+a[i]-a[i-2]);
    }
    cout<<dp[n]*2<<endl;
}
int main(){
    int T=1;
    cin>>T;
    while (T--){
        solve();
    }
    return 0;
}

F.Fraction Construction Problem

题意:

输入a,b,输出c,d,e,f
思路：1.gcd(a,b)!=1可直接输出答案,a/g+1,b/g,1,b/g
2.质因数种数只有1个或0个,输出-1,-1,-1,-1
3.否则利用exgcd来找正整数解，若无输出-1,-1,-1,-1

const int N=2e6+10;
int n,m,k,p;
int pre[N],vis[N],prim[N];	
void euler(int n){
    int num=0;
    pre[1]=1;
    for (int i=2;i<=n;i++){
        if (vis[i]==0){
            prim[++num]=i;
            pre[i]=i;
        }
        for (int j=1;j<=num&&prim[j]*i<=n;j++){
            vis[i*prim[j]]=1; 
            pre[i*prim[j]]=prim[j];
            if (i%prim[j]==0){
                break;
            }
        }
    }
}
int exgcd(int a,int b,ll &x,ll &y){    
    if(b==0){        
        x=1;y=0;return a;  
    }    
    int r=exgcd(b,a%b,x,y);
    int temp=y;y=x-(a/b)*y;x=temp;    
    return r;  
}
int gcd(int x,int y){
	return x%y?gcd(y,x%y):y;
}
void solve(){
    int a,b;
    cin>>a>>b;
    int g=gcd(a,b);
    if (g!=1){
    	printf("%d %d %d %d\n",a/g+1,b/g,1,b/g);
    	return;
    }
    n=b;
    ll s1=1,s2=1,f=pre[n];
    while(pre[n]!=n){
        if (pre[n]==f)s1*=pre[n];
        else s2*=pre[n];
        n/=pre[n];
    }
    if (n==f)s1*=n;
    else s2*=n;
    if (s1>s2)swap(s1,s2);
    if (s1==1||s2==1){
        printf("-1 -1 -1 -1\n");
    }
    else{
        ll x,y;
        exgcd(s2,-s1,x,y);
        if (y<=0){
            ll t=(y/s2+1);
            y+=t*s2;
            x+=t*s1;
        }
        if (x<=0){
            ll t=(x/s1+1);
            x+=t*s1;
            y+=t*s2;
        }
        if (x*s2<y*s1){
            swap(x,y);swap(s1,s2);
        }
        x*=a;y*=a;
        if (x<=0||y<=0)printf("-1 -1 -1 -1\n");
        else printf("%lld %lld %lld %lld\n",x,s1,y,s2);
    }
}
int main(){
    int T=1;
    euler(2e6);
    cin>>T;
    while (T--){
    	solve();
    }
    return 0;
}

G.Operating on a Graph

H.Sort the Strings Revision

I.Sorting the Array

J.Operating on the Tree

K.Eleven Game

L.Problem L is the Only Lovely Problem

超级签到题