2020牛客多校第二场By Rynar

A. All with Pairs

题意：n个字符串，两两之间的前后缀的最长相同值的平方和

#define Base 233
#define K 5
int n,m,k;
char s[M];
int cnt[M];
vector<int>nx[N];
ull Pow[M];
vector<ull>hs[N];
unordered_map<ull,int> mp;
void getnext(int id,char *p){
    int len=strlen(p);
    nx[id][0]=-1;
    int k=-1,j=0;
    while (j<len){
        if (k==-1||p[j]==p[k]){//p[k]表示前缀，p[j]表示后缀
	    nx[id][++j]=++k;
        }
        else k=nx[id][k];
    }
}
void handle(int id){
    int len=strlen(s);
    nx[id].resize(len+1);
    hs[id].resize(len+1);
    getnext(id,s);
    for (int i=1;i<=len;i++)
        hs[id][i]=hs[id][i-1]*Base+s[i-1]-'a'+K;
    for (int i=0;i<len;i++){
        ull t=hs[id][len]-hs[id][i]*Pow[len-i];//记录后缀的hash
        mp[t]++;
    }
}
int main(){
    Pow[0]=1;
    rep(i,1,M-1)Pow[i]=Pow[i-1]*Base;
    scanf("%d",&n);
    rep(i,1,n){
    	scanf("%s",&s);
    	handle(i);
    }
    int ans=0;
    rep(i,1,n){
        int len=int(hs[i].size())-1;
        rep(j,1,len){
            cnt[j]=mp[hs[i][j]];
            cnt[nx[i][j]]-=cnt[j];
        }
        rep(j,1,len)ans=(1ll*cnt[j]*j%mod*j+ans)%mod;
    }
    printf("%d\n", ans);
    return 0;
}

B. Boundary

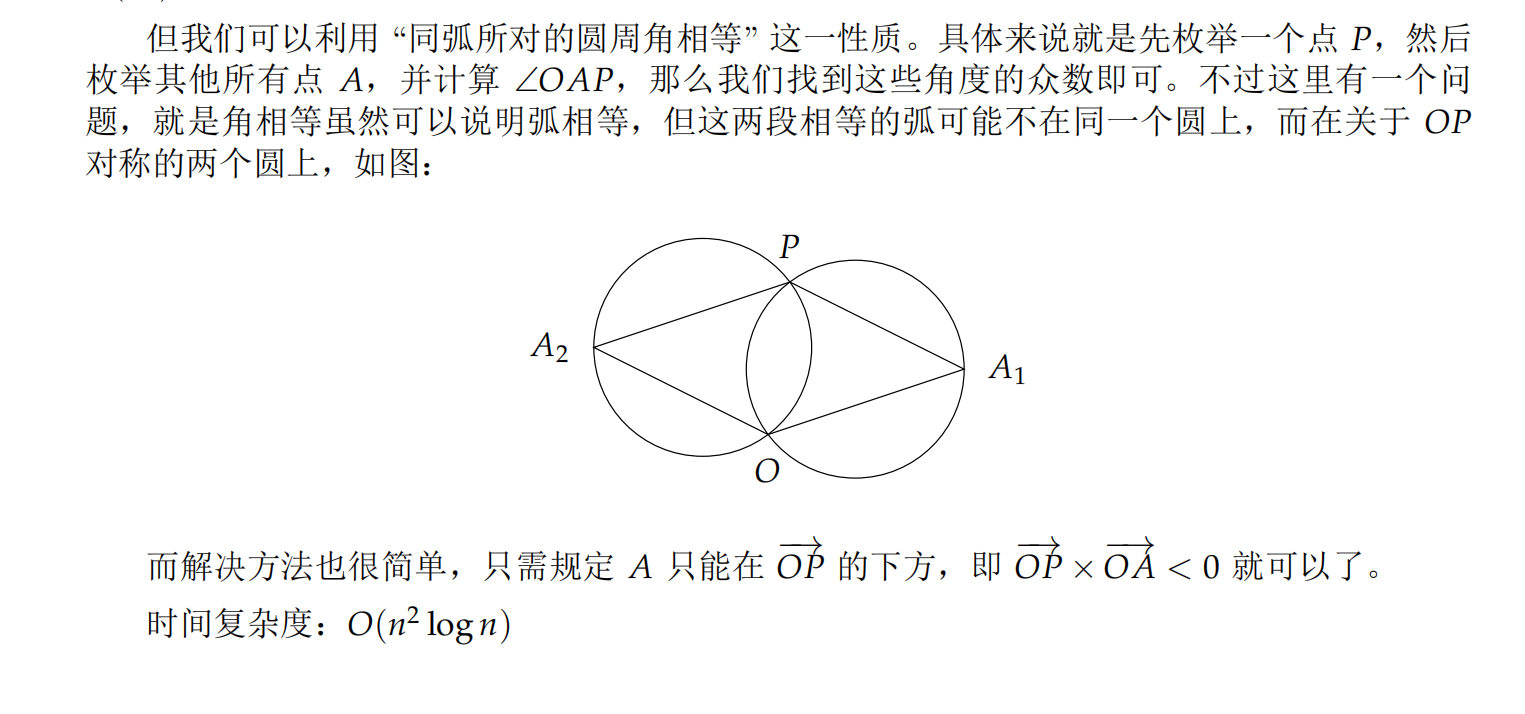
题意：给n个点，求过原点的圆，最多交多少个点

const int N=2e3+10;
const double eps=1e-11;
int n,m,k;
int x[N],y[N];
vector<double> p;
int main(){
    cin>>n;
    rep(i,1,n){
        cin>>x[i]>>y[i];
    }
    int ans=0;
    rep(i,1,n){
        p.clear();
        rep(j,1,n){
            if(i==j||x[i]*y[j]-x[j]*y[i]>=0) continue;
            double a=x[j]*x[j]+y[j]*y[j];
            double b=(x[j]-x[i])*(x[j]-x[i])+(y[j]-y[i])*(y[j]-y[i]);
            double c=x[i]*x[i]+y[i]*y[i];
            double d=(a+b-c)*abs(a+b-c)/(4.0*a*b);//cos^2
            p.pb(d);
        }
        sort(p.begin(),p.end());
        if(p.size())ans=max(1,ans);
        else continue;
        int s=0;
        rep(j,1,p.size()-1){
            if(fabs(p[j]-p[j-1])<eps)s++;
            else s=0;
            ans=max(ans,s+1);
        }
    }
    cout<<ans+1<<endl;
    return 0;
}

C. Cover the Tree

题意：给一棵树，问最少要多少链覆盖树的每一条边，输出条数和链的双端
我的思路：n>2时,找一度>1的点为根，dfs序依次记录度为1的点，把该序列平分成左右2区间，左右区间的从左到右依次相连，若有中点，连接根

const int N=2e5+10;
ll n,m,k;
vector<int>v[N],p;
int d[N];
struct node{
    int id,w;
}a[N];
bool cmp(node a,node b){
    return a.w<b.w;
}
void dfs(int x,int fa){
    if (d[x]==1)p.pb(x);
    for (int i:v[x]){
        if (i==fa)continue;
        dfs(i,x);
    }
}
int main(){
    int x,y,rt;
    cin>>n;
    rep(i,1,n-1){
        int x,y;
        cin>>x>>y;
        d[x]++;d[y]++;
        v[x].pb(y);v[y].pb(x);
    }
    if (n==1){
        cout<<0<<endl;
        return 0;
    }
    if (n==2){
        cout<<1<<endl;
        cout<<1<<" "<<2<<endl;
        return 0;
    }
    rep(i,1,n){
        if (d[i]!=1){
            rt=i;
            break;
        }
    }
    dfs(rt,-1);
    int s=p.size();
    cout<<(s+1)/2<<endl;
    rep(i,1,s/2){
        cout<<p[i-1]<<" "<<p[i+(s+1)/2-1]<<endl;
    }
    if (s&1){
        cout<<1<<" "<<p[s/2]<<endl;
    }
    return 0;
}

D. Duration

 超级签到题。

E. Exclusive OR

F. Fake Maxpooling

题意：n,m,k,求n*m上所有k*k区间中的最大的lcm(i,j)的和

const int N=5e3+10;
int n,m,k;
int b[N][N],l[N][N];//如果要求内存更少的话，b和l能共用 
deque<int>q;
int main(){
    cin>>n>>m>>k;
    rep(i,1,n){//O(nm)处理lcm
        rep(j,1,m){
            if (!l[i][j]){
                for (int k=1;k*i<=n&&k*j<=m;k++){
                    l[k*i][k*j]=i*j*k;//g[k*i][k*j]=k; 
                }
            }
        }
    }
    ll ans=0;
    rep(i,1,n){//单调队列,先处理行在处理列 
        while (!q.empty())q.pop_back();
        rep(j,1,k-1){
            while(!q.empty()&&l[i][q.back()]<=l[i][j])q.pop_back();
            q.push_back(j);
        }
        rep(j,k,m){
            if(!q.empty()&&q.front()<=j-k)q.pop_front();
            while(!q.empty()&&l[i][q.back()]<=l[i][j])q.pop_back();
            q.push_back(j);
            b[i][j]=l[i][q.front()];
        }
    }
    rep(j,k,m){
        while(!q.empty())q.pop_back();
        q.push_back(0);
        rep(i,1,k-1){
            while(!q.empty()&&b[q.back()][j]<=b[i][j])q.pop_back();
            q.push_back(i);
        }
        rep(i,k,n){
            if(!q.empty()&&q.front()<=i-k) q.pop_front();
            while(!q.empty()&&b[q.back()][j]<=b[i][j])q.pop_back();
            q.push_back(i);
            ans+=b[q.front()][j];
        }
    }
    cout<<ans<<endl;
    return 0;
}

G. Greater and Greater

题意：长n的序列A，长m的序列B，找出A的m长连续子序列S满足Si>=Bi

const int N=2e5+10;
bitset<N>f,g;
int n,m,k;
pii a[N],b[N];
bool cmp(pii a,pii b){
    return a.first>b.first;
}
int main(){
    cin>>n>>m;
    rep(i,1,n)sf(a[i].first),a[i].second=i;
    rep(i,1,m)sf(b[i].first),b[i].second=i;
    sort(a+1,a+1+n,cmp);
    sort(b+1,b+1+m,cmp);
    f.set();g.reset();
    int i=1,j=1;
    while (i<=m){
        while (j<=n&&a[j].first>=b[i].first)g.set(a[j++].second);
        f&=g>>b[i].second;//bitset使产生组合 
        i++;
    }
    cout<<f.count()<<endl;
    return 0;
}

H. Happy Triangle

I. Interval

思路：

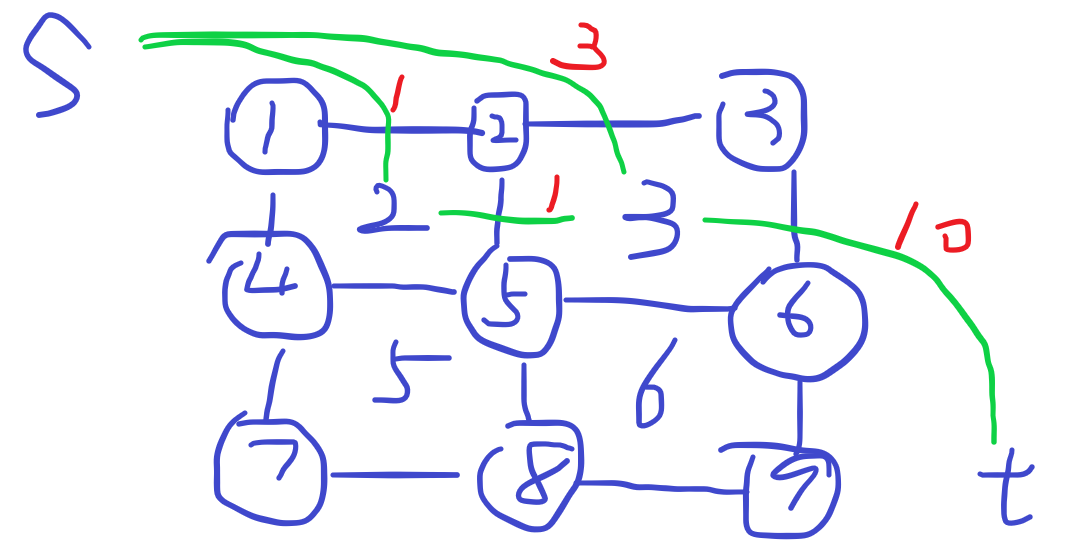
所求的即是右上角到左下角的最大流，可由对偶图的性质转换为求最短路，最短路为最小割，可以以右上角的点标号作为区块的标号，如图样例1。

typedef long long ll;
typedef pair<ll,ll>P;
const int N=500+10;
const int M=N*N;
const ll inf=1e16;
int n,m;
ll c[M];
vector<P>v[M];
void dijkstra(int x){
    priority_queue< P , vector<P> , greater<P> > q;
    fill(c,c+n*n+1,inf);
    c[x]=0;
    q.push({0,x});
    while(!q.empty()){
        P r=q.top();
        q.pop();
        int u=r.second;
        if (c[u]<r.first)continue;
        for (auto i:v[u]){
            int to=i.first,d=i.second;
            if(c[u]+d<c[to]){
                c[to]=c[u]+d;
                q.push({c[to],to});
            }
        }
    }
}
void add(int x,int y,int z){
    v[x].push_back({y,z});v[y].push_back({x,z});
}
int main(){
    scanf("%d%d",&n,&m);
    int cnt=0;
    int s=0,t=n*n;
    while (m--){
        int x,y,z;char c;
        scanf("%d %d %c %d",&x,&y,&c,&z);
        int xx=(x-1)*n+y;//作为对偶图的右上角
        if (c=='L'){
            if (y==n)add(xx,t,z);
            else if (y==1)add(xx+1,s,z);
            else add(xx,xx+1,z);
        }
        else{
            if (x==1)add(s,xx,z);
            else if (x==n)add(xx-n,t,z);
            else add(xx,xx-n,z);
        }
    }
    dijkstra(s);
    if (c[t]==inf)puts("-1");
    else printf("%lld\n",c[t]);
    return 0;
}

J. Just Shuffle

题意：已知长为n的序列{1,2,...,n}，置换次数，置换后的序列，求置换规则
我的思路：产生的序列是k次置换产生的结果，对该序列按k次置换的规则置换一次产生2k次置换的序列，进行一次置换循环节和产生的序列循环节一样设为s，那么对原序列按照k次置换序列的规则进行1/k(%s)次置换会变为1次置换的结果，也就是置换规则序列，只需对每个循环节都进行这种操作即可

const int N=2e5+10;
int n,m,k;
int a[N];
int vis[N],b[N];
void ex_gcd(int a,int b,int &x,int &y){
    if (!b){x=1,y=0;return;}
    ex_gcd(b,a%b,x,y);
    int t=x;x=y;y=t-(a/b)*y;
}
int inv(int a,int p) {
    int inv_a,y;ex_gcd(a,p,inv_a,y);return (inv_a%p+p)%p;
}
int main(){
    scanf("%d%d",&n,&k);
    bool f=0;
    rep(i,1,n)scanf("%d",&a[i]);
    rep(i,1,n){
        if (!vis[i]){
            vector<int>v;
            int p=i;
            while (!vis[p])vis[p]=1,v.pb(p),p=a[p];
            int s=v.size(),t=k%s;
            t=inv(t,s);
            rep(i,0,s-1)b[v[i]]=v[(i+t)%s];
        }
    }
    rep(i,1,n)printf("%d",b[i]);
    puts("");
    return 0;
}

K. Keyboard Free

题意：有同心圆3个，半径为r1,r2,r3,三圆上各有一点，求三点组成的三角形面积的期望值

const int N=1e5+10;
const int K=1000;
const double pi=acos(-1.0);
int n,m,k;
int main(){
    int r1,r2,r3,T;
    cin>>T;
    while (T--){
        int x,y,z;
        cin>>x>>y>>z;
        r3=max(x,max(y,z));
        r1=min(x,min(y,z));
        r2=x+y+z-r1-r3;
        double x1=r1,y1=0.0,ans=0.0;
        for (int i=0;i<K;i++){
            double theta=2*pi*i/K;
            double x2=r2*cos(theta),y2=r2*sin(theta);
            double a=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
            if (a<=0.00000001)continue;
            double d=r1*y2/a;
            double alp=asin(d/r3);
            ans+=0.5*a*(2.0*d*alp+2.0*r3*cos(alp))/pi;
        }
        ans/=K;
        printf("%.1lf\n",ans);
    }
	return 0;
}