关于Manacher

Manacher算法

应用：在O（n）的时间复杂度内快速求出一个字符串中每个位置的最长回文串长度。
原理：我们先考虑暴力如何解决这个问题，直接枚举每个字符然后以此为中心向两边扩散，直到找到第一个不一样的字符再将中心字符向后枚举，在全A串时可以卡到最差复杂度O（n^2）。我们考虑通过是否可以通过已知信息的特殊性质来推出接下来的信息。
我们考虑现在枚举s到的回文中心位置为c，最长回文半径为R[i],那么根据回文串的性质s[c - R[i] + 1] = s[c + R[i] - 1]，考虑将这个性质进行拓展，那么我们假设c右边k个长度后有一个长度为|v|的回文串v，那么根据回文串的性质，c左边也一定有一个长度为|v|的回文串rev（v），我们再考虑如果此时v右边距离c+R[i]-1长度已经小于rev（v）的半径，肯定是先取c + R[i] - 1 - i + 1为v半径（i为v的中心字符串）。
如下图：

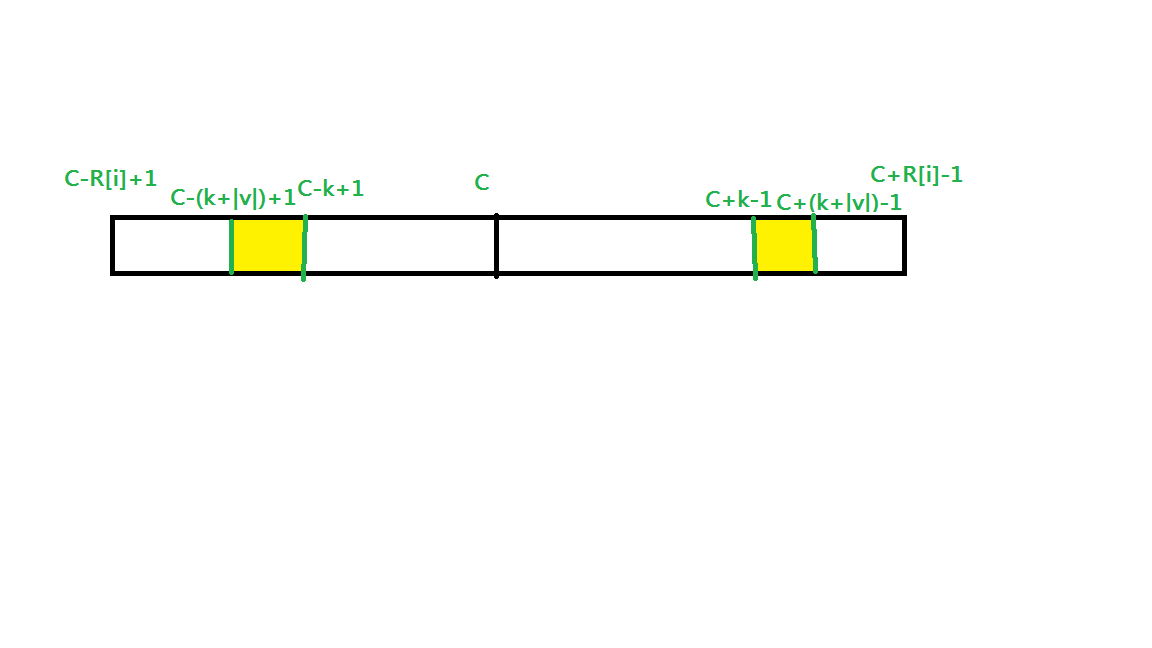
实现的话我们考虑现将字符串通过填充将回文中心都用一个字符来表示，然后每一次枚举下标时，判断现在的下标是否大于枚举到的最右的r，大于就更新R[i] = 1,否则将R[i]根据以上结论更新为min(r - i + 1,R[2*c - i])。

代码实现如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int const maxn = 2.2e7+10;
int R[maxn];
string s,t;
int ans;
signed main(){
	cin >> s;
	s = "@" + s;
	int n = s.size()-1;
	t+="!@";
	for(int i = 1;i <= n;i ++){
	    t+=s[i];
	    t+="@";
	}
	t+="#";
	n = t.size() - 1;
	for(int i = 1,r = 0,c = 0;i < n;i ++){
		if(i < r){
			R[i] = min(r- i + 1,R[2*c - i]);
		}else {
			R[i] = 1;
	    }
		while(t[i + R[i]]==t[i-R[i]]){
			R[i]++;
		}
		ans = max(ans,R[i]-1);
		if(i + R[i] - 1 > r){
			r = i + R[i] - 1;
			c = i;
		}
	}
	cout << ans;
	return 0;
}

另外Manacher所获取的这个最长回文长度还可以有其他的作用，如最长双回文字符串中我们可以通过求最长回文长度时，更新r的过程中维护以某个字符结尾，或以某个字符开头的最长回文串长度。