关于KMP算法

KMP（Knuth–Morris–Pratt）算法

该算法用于在O（n）的时间内找到多个串内搜索一个目标子串的位置

思路：我们先考虑如何暴力找一个串内所有目标子串的位置，很显然，我们只需要遍历每个串的每个字符，然后暴力check这个字符作为起始所形成的目标长度的串是不是目标串即可。
考虑优化，我们这样暴力查找之所以使时间很大是因为对于一个起始位置，我明明已经遍历过后面的串的信息了，却还重复遍历已获得过的信息，那我们可以考虑能不能将从遍历过的信息中获取有效信息使得我们在算后面的位置时可以利用这些信息来减少无效遍历，或是我们并不重复遍历这个大串，而是将小串与大串比的位置进行改变。因为我们发现每一次遍历失配后，我们就从头开始遍历小串跟大串一起比，若是能将小串位置不直接提前到开头，而是一个相对较近的位置，那我们是不是就能省下来很多无效次数。这时候我们考虑用一个方式来存储小串位置可以转移到的前面的位置。
我们考虑小串假如在k位置与大串不相同，那小串前面的串都应该和大串对应相同，那么我们能否把k转移到前面的位置时，同时保证转移到的位置前面的串和现在位置前面的串最大位置相等。
我们考虑用一个函数来表达这个转移。
对于一个字符串s[0_{n]，设π（i）表示s[0}i]这个字符串真前缀与真后缀相等的最长的长度（真的意思就是不包括全集），例如对于ababbab
π（0） = 0
π（1） = 0
π（2） = 1，“a”
π（3） = 0
π（4） = 0
π（5） = 2,“ab”
π（6） = 0
这个函数就能实现我们所需要的目标，若我们已经求出这个函数，那么考虑每一次遇到失配的字符，我们直接转移，之后再暴力匹配即可。
分析时间复杂度等会介绍完π（i）后做
考虑对于一个π函数，假设我们已经算出来了π（i），算π（i+1）时若没有失配，则直接更新π（i+1） = π（i） + 1
否则我们考虑将i转移到前面的使s[0~j]与s[i-j ~ i]相同的j
我们可以通过如下的图来分析性质

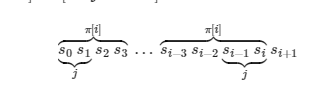
容易得到这样一个等式
s[0~j-1] = s[i-j+1 ~ i] = s[j~2 * j - 1] = s[π（i）-j ~ π（i）-1]
也就是说j实际上是s[0~π(i)-1]的函数值
即j = π(π(i) - 1)
由此我们可以很快的处理出来π（i）的值
现在我们来分析复杂度
对于匹配串，我们有三种情况：
1.匹配，则直接两个串向前继续遍历
2.小串位于第一个字符且不匹配，那么大串向前遍历
3.小串向后退，最多不退n次
所以时间复杂度为O（n）
对于求π情况与上类似，时间复杂度为O(m)
总复杂度为O（n+m）
代码实现：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int const maxn = 1e6+10;
int pi[maxn];
string s1,s2;
int ans[maxn],cnt;
signed main(){
	cin >> s1 >> s2;
	s1 = "@" + s1;
	s2 = "@" + s2;
	int j = 0;
	for(int i = 2;i <= s2.size()-1;i ++){
		while(j > 0&&s2[i]!=s2[j+1])j = pi[j];
		if(s2[i]==s2[j+1])j++;
		pi[i] = j; 
	}
	j = 0;
	for(int i = 1;i <= s1.size()-1;i ++){
		while(j > 0&&s1[i]!=s2[j+1])j = pi[j];
		if(s1[i]==s2[j+1])j++;
		if(j==s2.size()-1){
			cout <<  i - j + 1<<'\n';
			j = pi[j];
		}
	}
	for(int i = 1;i <= s2.size()-1;i ++){
		cout << pi[i]<<' ';
	}
	return 0;
}

关于这个π（i）函数，名字叫做前缀函数，并且这个函数还有其他强力的作用如下

求字符串周期

对于一个串s,若存在0<r<|s|是的s的长度为r的前缀和后缀相同，称s的长度为r的前缀是s的border，由此便可推出|s| - r是|s|的周期（画一下图划分一下区域就能理解）,π（|s|-1）是s最长border的长度。
我们可以在O（n）时间内求出S的所有周期长度

求某串的所有前缀在某个串分别出现的次数

根据前缀函数定义，我们可以对于每个π（i），其必定在i为右端点时出现一次，并且对于π(i-1)，也一定在π(i)的答案中出现了，并且每个前缀一开始都出现一次。那么我们先将所有的π（i）的答案进行统计，然后倒序枚举n，将π(i)的答案加到π(i-1)中，最后再把每个前缀的出现次数都加一即可