Solution -「GLR-R3」春分 & Talk - 题解中的“动机”

  （大致是从某次讲课的 beamer 改过来的，所以可能存在一些神秘的分段。）

题意

  Link. (难以概括的.)

分享目的 & 提示

分享目的

  这是一道我和 @Reanap 合作完成的奇幻构造题, 受到 @ix35, @Alex_Wei 等人的好评.

  用出题人视角让你相信: 构造题是可做且好玩儿的.

 

提示

  先试试构造 \(m\approx 2n\)? 再试试 \(m\approx\frac{3}{2}n\)?

  你是否感受到已有方案缺点? 试着描述缺点, 思考如何避免它们.

  注意样例 \(n=2\) 的精妙构造, 虽然不能直接扩展, 但也有一定启发意义.

  (做题人才有的提示: 猜测数据范围中 \(m\) 和 \(n\) 的数量关系.)

目标分析

  或许你得到了 \(m\approx\frac{3}{2}n=\frac{1}{2}n+n\) 的构造:

  → Solution to Subtask #3 \(m=\frac{3}{2}n+\mathcal O(1)\):

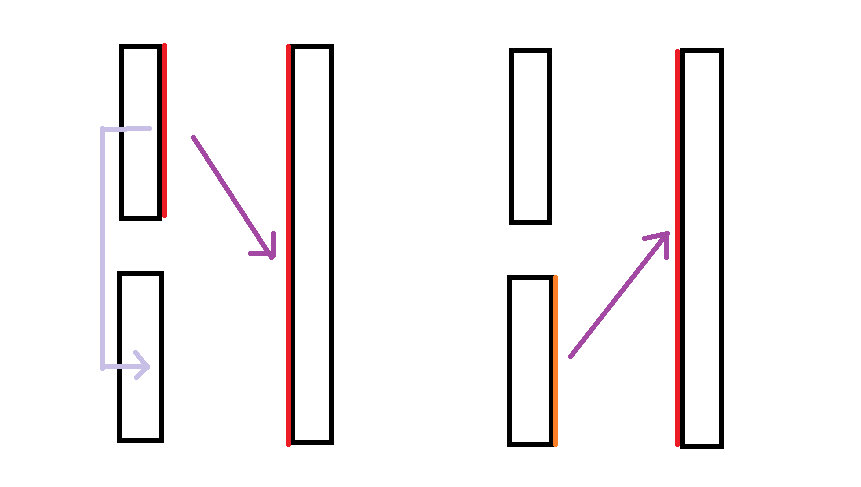
  它有一个很明显的问题: 橙色 \(\times\) 红色中, 橙色面是脏的 (沾染了其他溶液) 而红色面是干净的, 这样我们白白浪费了 \(n\) 个干净的面!

  Reanap 的官方题解中提到了相同的动机: "最劣的地方是, 我们用板的脏面去触碰了板的干净面, 这种行为我们认为是极其不优秀的, 我们带着这种想法去构造更优方案."

  例如, 可以尝试让右侧红色面也经历一些翻转, 有效利用它们的干净面. 再例如, 如何保护干净面不受污染呢? 看看样例?

初步优化

  或许你又得到了 \(m\approx\frac{4}{3}n=\frac{1}{3}n+n\) 的构造:

  → Solution to Subtask #4 \(m=\frac{4}{3}n+\mathcal O(1)\):

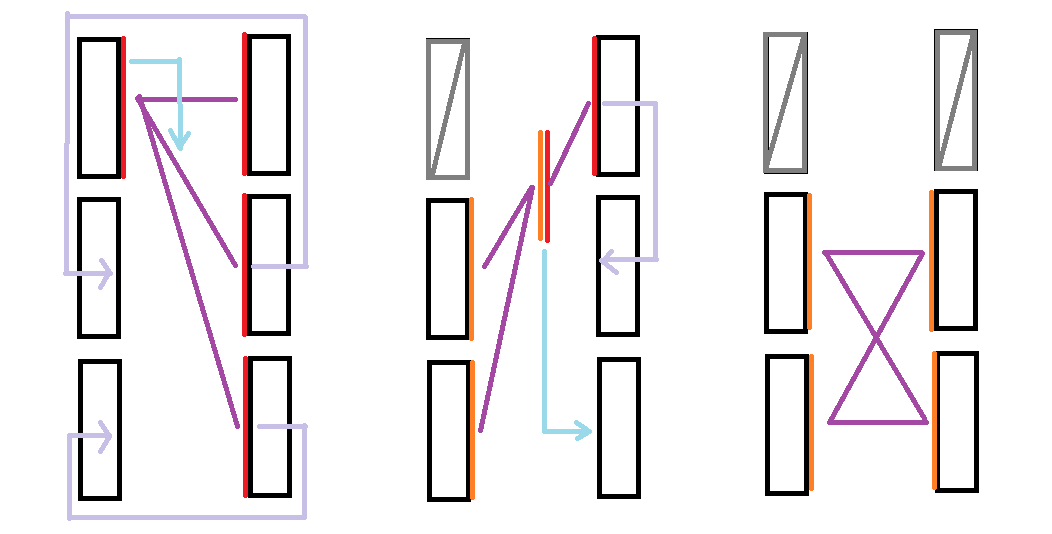
  这个构造又有什么缺点?

  ——的确, 没有哪个干净面因为直接和脏面接触而浪费. 但是第二步中, 被放在中间的橙色面本来是 "不太脏" 的: 虽然沾染了溶液, 但只沾染了特定的一种溶液. 第二步之后, 它们却沾染了多种溶液, 不可能再发挥作用了.

  那么, 放在中间 \(\frac{1}{3}n\) 块板都是有必要的吗?

神奇的板

  中间用一个板做保护就够了!

  另外, 还可以通过已有方案的形式找找规律. 我们先后得到了 \(n+n\), \(\frac{1}{2}n+n\), \(\frac{1}{3}n+n\), 那么 \(\frac{1}{4}n+n\) 会是一个不错的尝试.

  → Solution to Subtask #5 \(m=\frac{5}{4}n\pm\mathcal O(1)\) by Reanap:

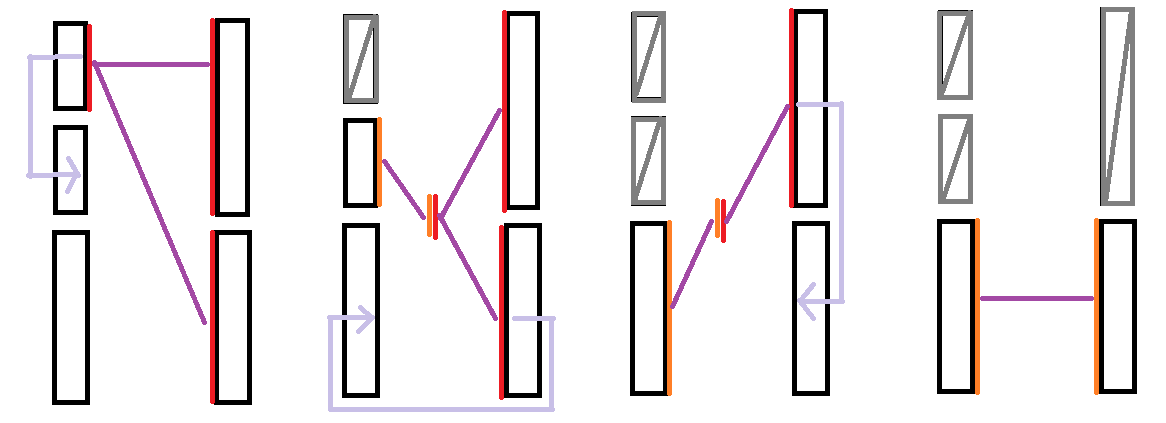
小插曲

  \(\frac{5}{4}n\pm\mathcal O(1)\) 一度被我们当做最优解. 不过现在, 我们至少有三种方法通向目前的最优解:

• a. 人类智慧 \(\to\) 我获得标算的方式;
• b. 数据范围观察和猜测 \(\to\) 对做题者最容易的方式;
• c. 数理分析与推理 \(\to\) 高三摸鱼科研成果.

  从出题人的视角来说, (a) 没法分享, (b) 不可实施, 我们来讲讲 (c).

抽象与转化

符号化描述

  问题的基本对象是板, 我们的首要任务是描述板的状态. 利用刚才的经验, 板的某一面有以下三种可能的状态:

• \(\text{C(lean)}\): 未沾染过溶液;
• \(\text{O}_x\text{(ccupied)}\): 只沾染过溶液 \(x\), 相当于被它占用;
• \(\text{M(essy)}\): 沾染过至少两种溶液, 纯纯的废物.

  一个板的状态可以用它两面的状态描述. 例如, \(\frac{5}{4}n\) 方案中的 "神奇的板" 在足够多次使用后, 会变为 \(\text M/\text C\) 的状态: 一面沾染了各种脏东西, 另一面保持干净, 而 \(\text C\) 面就起到了保护其他 \(\text C\) 面的作用.

  板的基本行为是接触. 接触后, 面状态的转换关系如下:

\[ \begin{array}{c|cccc} & \text C & \text O_x & \text O_y & \text M \\ \hline \text C & \text C & \text O_x & \text O_y & \text M^* \\ \text O_x & \text O_x & \text O_x & \text M & \text M \\ \text O_y & \text O_y & \text M & \text O_y & \text M \\ \text M & \text M^* & \text M & \text M & \text M \end{array} \]

如果默认使用一个 \(\text C/\text M\) 作保护, 那么在两个 \(\text M^*\) 处, 两个面接触前后的状态实际上不改变.

 

性质挖掘

性质 A

  匹配 (一次实验) 中, 没有必要在两个板间夹一个 \(\text C/\text C\).

  → Proof. 需要一点分讨.

• \(\star/\text C\sim\text C/\text C\sim\text C/\star\), 中间这个板可以省略.
• \(\star/\text C\sim\text C/\text C\sim\text M/\star\), 不如用 \(\text C/\text M\).
• \(\star/\text C\sim\text C/\text C\sim\text O_x/\star\), 这样做的目的只能是保护 \(\text O_x\). 但是不如直接用 \(\text C/\text C\) 代替右侧这个板. 直观上说, \(\text C\) 的价值是高于 \(\text O_x\) 的, 这样不值得.
• 其他情况类似, 略过.

性质 B

  如果给溶液 \(x\) 分配了初始的板 \(\text O_x/\text C\), 则一旦这个板从紧贴 \(x\) 的状态移开 (即不再以 \(x\sim\text O_x/C\) 的形式参与匹配), 它等效于立即变为 \(\text M/\text O_y\).

  → Proof. 首先, 它的 \(\text O_x\) 面一定会变为 \(\text M\), 这是因为 \(\text O\) 与 \(\text C\) 贴不优, 那么在排除 \(x\sim\text O_x/C\) 的情况下 \(\text O_x\) 必然被 \(\text O_z\) 或者 \(\text M\) 污染. 其次, \(\text C\) 面一定会立即被某溶液 \(y\) 占用, 不然没有必要献祭 \(\text O_x\) 来参与这次匹配.

推论 C

  在初始的板分配完成后, 场上只有三类板: 一个辅助板 \(\text C/\text M\), 一些在初始分配位置的板 \(\text O_x/\text C\), 一些转移过位置的板 \(\text O_y/\text M\).

 

问题转化

  根据推论 C, 发现一个重要的性质: 我们根本不需要知道 \(\text O_x\) 状态中的 \(x\) 是谁. 再根据面状态的转换关系, 所有有必要的接触其实都不会改变 (除辅助板之外的) 任何面的状态!

  因此, 原问题不强于:

转化问题

  左右两侧各有 \(n\) 个盒子, 初始时你可以在每个盒子中放上至多一个小球, 每个小球可以由一个盒子移动向另一个空盒子, 但同一个小球至多移动一次. 构造方案, 使得在移动过程中, 对于任意左侧盒子 \(x\) 和右侧盒子 \(y\), 都存在一个时刻, 它们中都有小球.

数学推导

  当操作的自由度足够低, 我们可以逐步引入数学模型来描述.

猜想

  存在一种最优方案, 其中所有小球都在同侧移动. 即不会有左侧 (右侧) 盒子里的小球移动到右侧 (左侧).

  猜想由来: 这符合我们目前得到的最优解; 而允许异侧移动时, 我没能够进行足够好的定量描述, 也没法给出下界.

  接下来, 我们推证同侧移动限制下, 转化问题的理论最优解. 考虑初始状态中一对左右小球的贡献:

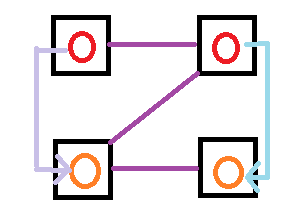
  一对小球至多贡献三次匹配.

  假设左右两侧初始有 \(pn\) 和 \(qn\) 个球, 忽略常数, 我们可以把 \(n\) 当做 \(1\) 而用比例 \(p\) 和 \(q\) 来描述球数和匹配数. 根据已有要求, 我们可以写下一些限制:

\[p\ge\frac{1}{2},\quad q\ge\frac{1}{2},\quad 3pq\ge 1. \]

  不过, 一些冗余的贡献是无法忽略的. 例如对于左侧:

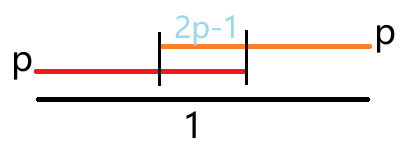
  红色表示初始小球, 橙色表示移动后小球, 可见红橙间必然产生占比为 \(2p-1\) 的重叠. 红球进入重叠位置的时刻 (即初始时刻) 和橙球进入重叠位置的时刻, 对应了右侧小球的两组位置状态. 不管这两个状态长什么样子, 同样也至少有 \(2q-1\) 的重复! 这样, 就至少会产生 \((2p-1)\times(2q-1)\) 的冗余贡献.

  现在的任务是:

\[ \begin{array}{rl} \text{minimize} & p+q,\\ \text{s.t.} & \begin{cases} p\ge 1, \\ q\ge 1, \\ 3pq-(2p-1)(2q-1)\ge 1. \end{cases} \end{array} \]

  这是纯数学问题了. 极值 \(p=q\) 处的结果不如边界; 边界上 \(p=\frac{1}{2}\) 解得 \(q=\frac{2}{3}\), 得到 \((p+q)_{\min}=\frac{7}{6}\). 我们只需要构造一个 \(m=\frac{1}{2}n+\frac{2}{3}n\pm\mathcal O(1)\) 的解就行了.

最终构造

  → Solution to Subtask #7 \(m=\frac{7}{6}n\pm\mathcal O(1)\) by Rainybunny:

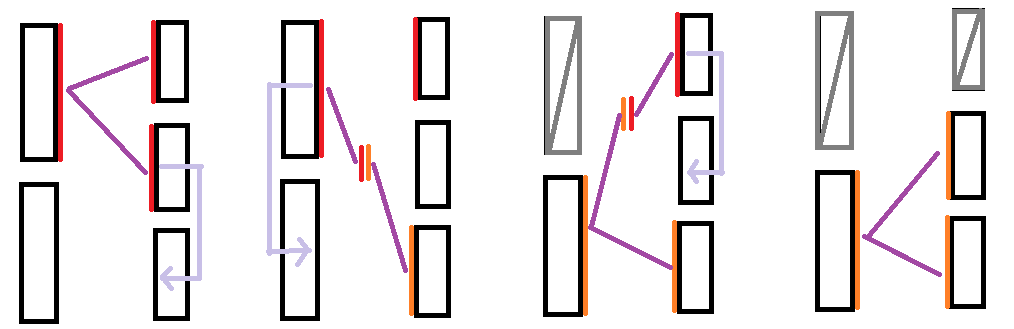
题解之外：题解中的“动机”

  这段是无聊的论述，所以改用中文标点。你或许觉得很奇怪，嗯呐我也觉得（雾）。

  其实所谓“题解”只需要最后这张图，但是你的确需要像出题人一样知道它是如何一步步推出来的。构造题恐惧症解药推荐：https://www.cnblogs.com/rainybunny/p/15398779.html。你可以见到更多和这里同样细致的构造题解析和思维探讨。

  遗憾的是，作为一道题目，它一定存在数据范围，也一定存在对应数据范围下的正确答案。大部分做题者是没有办法和出题者一样体验钻研 open problem 的感受的。更遗憾的是，对于一道构造题，“想出答案”或许很难，“看懂答案”几乎总是小菜一碟：仅仅花半分钟欣赏上面这张图就能获得一个 Accepted——同时永远失去一个“未被知识污染”的大脑。

  所以，或许只是作为一个倡议，我希望在题解中看到每个“注意到”背后的动机。尝试感知、复现并记录自己“想出思路”的元思考过程，并把它毫无保留地展现给没能独立做出题目的人，让他们看完题解后感叹“原来这种题可以朝这个方向思考”而不是惊呼“这是人类能想到的吗？”。说到底“题解”也不是论文，也并不是在展现 sota，它的目的就是让人看懂而不是让人知道“这道题的解法存在”，那何必把思考的脚手架拆掉，然后假装自己是注意力仙人呢？

  这些观点或许值得展开聊聊，但我要品尝 malloc lab，就先这样了√