数学分析（2022暑假特辑）

“如果你也在迷茫的话，不妨从现在开始，滴水穿石，积少成多”

<新知识>

欧氏空间：设 \(V\) 是实数域 \(\mathbb R\) 上的线性空间，在 \(V\) 上任意两向量 \(x,y\) 按某一确定法则对应于唯一确定的实数，称为内积，记为 \((x,y)\)，满足以下性质：
1)对称性 \((x,y)=(y,x)\)
2)可加性 \((x+y,z)=(x,z)+(y,z)\)
3)齐次性 \((kx,y)=k(x,y)\)，\(k\) 为任意实数
4)非负性 \((x,x)\geq0\)，当且仅当 \(x=0\) 时有 \((x,x)=0.\)
定义了内积的实线性空间 \(V\)，叫实内积空间即欧氏空间。

酉空间：设 \(V\) 是复数域 \(\mathbb C\) 上的线性空间，在 \(V\) 上任意两向量 \(x,y\) 按某一确定法则对应于唯一确定的复数，称为内积，记为 \((x,y)\)，满足以下性质：
1)共轭对称性 \((x,y)=\overline{(y,x)}\)
2)可加性 \((x+y,z)=(x,z)+(y,z)\)
3)齐次性 \((kx,y)=k(x,y)\)，\(k\) 为任意复数
4)非负性 \((x,x)\geq0\)，当且仅当 \(x=0\) 时有 \((x,x)=0.\)
定义了内积的复线性空间 \(V\)，叫复内积空间即酉空间。
例：酉空间中向量 \(\alpha=(a_1,\cdots,a_n),\beta=(b_1,\cdots,b_n)\)，内积为

\[(\alpha,\beta)=a_1\overline{b_1}+\cdots+a_n\overline{b_n} \]

Hermite 矩阵：自共轭矩阵，第 \(i\) 行第 \(j\) 列的元素都与第 \(j\) 行第 \(i\) 列的元素的共轭相等，主对角线上的元素都是实数，特征值也是实数。

Gram 矩阵：内积矩阵，向量两两内积组成的矩阵。它是半正定 Hermite 矩阵，若向量组线性无关则为正定 Hermite 阵。
例：基 \(\{\beta_1,\cdots,\beta_n\}\) 的 Gram 矩阵为

\[\left[\begin{matrix} (\beta_1,\beta_1)&\cdots&(\beta_1,\beta_n)\\ \vdots&\ddots&\vdots\\ (\beta_n,\beta_1)&\cdots&(\beta_n,\beta_n) \end{matrix}\right] \]

\(1.\quad\) 设 \(\alpha_1,\alpha_2,\cdots,\alpha_n\) 是 \(V\) 的一组标准正交基，证明：\(\forall x\in V\)，成立 \(x=(x,\alpha_1)\alpha_1+\cdots+(x,\alpha_n)\alpha_n.\)

设 \(x=k_1\alpha_1+\cdots+k_n\alpha_n\)，将 \(x\) 与 \(\alpha_i\) 作内积 \((x,\alpha_i)=k_i(\alpha_i,\alpha_i)=k_i\)，因此得证。

\(2.\quad\) 设 \(\{e_1,\cdots,e_n\},\{f_1,\cdots,f_n\}\) 是 \(V\) 的两组基，\(C\) 是从 \(\{e_1,\cdots,e_n\}\) 到 \(\{f_1,\cdots,f_n\}\) 的过渡矩阵，基 \(\{e_1,\cdots,e_n\}\) 的 Gram 矩阵为 \(G\)，证明基 \(\{f_1,\cdots,f_n\}\) 的 Gram 矩阵为 \(H=C'G\overline{C}.\)

由过渡矩阵的定义，\((e_1,\cdots,e_n)C=(f_1,\cdots,f_n)\)，因此 \(f_j=\displaystyle{\sum_{i=1}^nc_{ij}e_i}\)，于是

\[\begin{aligned} H(i;j)=&(f_i,f_j)\\ =&(\displaystyle{\sum_{k=1}^nc_{ki}e_k},\displaystyle{\sum_{l=1}^nc_{lj}e_l})\\ =&\sum_{k=1}^n \sum_{l=1}^n c_{ki}\overline{c}_{lj}(e_k,e_l)\\ =&\sum_{k=1}^n c_{ki} \sum_{l=1}^n g_{kl}\overline{c}_{lj}\\ =&\sum_{k=1}^n C'(i;k)\cdot(G\overline C)(k;j)\\ =&C'G\overline C(i;j) \end{aligned} \]

因此

\[H=C'G\overline{C} \]

\(3.\quad\) 设 \(H\) 是一个 \(n\) 阶正定 Hermite 矩阵，证明必存在 \(V\) 的一组基 \(\{f_1,\cdots,f_n\}\) 使得它的 Gram 矩阵就是 \(H.\)

取一组基 \(\{e_1,\cdots,e_n\}\)，其 Gram 矩阵为 \(G\)，它也是正定 Hermite 阵，那么 \(G\) 与 \(H\) 相合：

\[H=C'G\overline C \]

由上一题的结论，令 \((f_1,\cdots,f_n)=(e_1,\cdots,e_n)C\) 即可。

\(4.\quad\) \(\displaystyle{\int \frac{1+\ln(\sqrt{x+1}+\sqrt{x-1})}{\sqrt{x^2-1}(\sqrt{x+1}-\sqrt{x-1})}\text dx}\)

采用双元法。\(p=\sqrt{x+1},q=\sqrt{x-1}\)

\[\begin{aligned} &\int \frac{1+\ln(\sqrt{x+1}+\sqrt{x-1})}{\sqrt{x^2-1}(\sqrt{x+1}-\sqrt{x-1})}\text dx\\ =&2\int\frac{1+\ln(p+q)}{q(p-q)}\text dp\\ =&2\int\frac{1}{p-q}\frac{\text dp}{q}+2\int\frac{\ln(p+q)}{p-q}\frac{\text dp}{q}\\ =&-2\int\frac{1}{p-q}\frac{\text d(p-q)}{p-q}+2\int\frac{\ln(p+q)}{p-q}\frac{\text d(p+q)}{p+q}\\ =&\frac{2}{p-q}+(p+q)\ln(p+q)-(p+q) \end{aligned} \]

\(5.\quad\) 证明 Frullani 定理：若 \(f\in C[0,+\infty)\)，且 \(\displaystyle{\lim_{x\rightarrow +\infty}f(x)=0},a,b>0\)，则

\[\int_0^{+\infty} \frac{f(ax)-f(bx)}{x} \text dx=f(0)\ln\frac{b}{a} \]

\[\begin{aligned} \int_M^{N} \frac{f(ax)-f(bx)}{x} \text dx=&\int_M^{N} \frac{f(ax)}{x} \text dx-\int_M^{N} \frac{f(bx)}{x} \text dx\\ =&\int_{aM}^{aN}\frac{f(x)}{x}\text dx-\int_{bM}^{bN}\frac{f(x)}{x}\text dx\\ =&\int_{aM}^{bM}\frac{f(x)}{x}\text dx-\int_{aN}^{bN}\frac{f(x)}{x}\text dx\\ =&f(\xi)\int_{aM}^{bM}\frac{1}{x}\text dx-f(\eta)\int_{aN}^{bN}\frac{1}{x}\text dx\\ =&(f(\xi)-f(\eta))\ln\frac{b}{a} \end{aligned} \]

令 \(M\rightarrow0,N\rightarrow+\infty\)，则 \(f(\xi)\rightarrow f(0),f(\eta)\rightarrow 0\)，因此

\[\int_0^{+\infty} \frac{f(ax)-f(bx)}{x} \text dx=f(0)\ln\frac{b}{a} \]

\(6.\quad\) 计算 Fejér 积分：

\[\int_0^\frac{\pi}{2} \frac{\sin^2 nx}{\sin^2x}\text dx \]

设 \(\displaystyle{a_n=\int_0^\frac{\pi}{2} \frac{\sin^2 nx}{\sin^2x}\text dx}\)，则 \(\displaystyle{a_{n-1}=\int_0^\frac{\pi}{2} \frac{\sin^2 (n-1)x}{\sin^2x}\text dx}\)

\[\begin{aligned} a_n-a_{n-1}=&\int_0^\frac\pi2 \frac{(\sin nx+\sin(n-1)x)(\sin nx-\sin(n-1)x)}{\sin^2x}\text dx\\ =&\int_0^\frac\pi2 \frac{2\sin\frac{2n-1}{2}x\cos\frac{x}2\cdot2\cos\frac{2n-1}{2}x\sin\frac{x}2}{\sin^2x}\text dx\\ =&\int_0^\frac\pi2 \frac{\sin(2n-1)x}{\sin x}\text dx \end{aligned} \]

我们熟知

\[\frac{\sin(2n-1)x}{\sin x}=2\sum_{k=0}^{n-1}\cos(2kx)+1 \]

因此

\[\begin{aligned} a_n-a_{n-1}&=\frac{\pi}{2}\\ a_n&=\frac{n\pi}{2} \end{aligned} \]

<新知识>

Kronecker delta 符号：

\[\delta_{ij}=\begin{cases} 1,i=j\\ 0,i\ne j \end{cases} \]

Levi-Civita 符号：

\[\varepsilon_{ijk}=\begin{cases} 0,\quad\text{if any two labels are the same}\\ 1,\quad\text{even permutation}\\ -1,\quad\text{odd permutation} \end{cases} \]

例：

\[\varepsilon_{ijk}\varepsilon_{mnl}=\left|\begin{matrix} \delta_{im}&\delta_{in}&\delta_{il}\\ \delta_{jm}&\delta_{jn}&\delta_{jl}\\ \delta_{km}&\delta_{kn}&\delta_{kl} \end{matrix}\right| \]

\(7.\quad\) 证明 \(\boldsymbol u\times(\boldsymbol v\times \boldsymbol w)=\boldsymbol v(\boldsymbol u\cdot \boldsymbol w)-\boldsymbol w(\boldsymbol u\cdot \boldsymbol v)\)

\[\begin{aligned} \boldsymbol u\times(\boldsymbol v\times \boldsymbol w)=&\varepsilon_{ijk} u_i\varepsilon_{mnj}v_mw_n\boldsymbol e_k\\ =&(\delta_{in}\delta_{km}-\delta_{im}\delta_{kn})u_iv_mw_n\boldsymbol e_k\\ =&u_iv_kw_i\boldsymbol e_k-u_iv_iw_k\boldsymbol e_k\\ =&\boldsymbol v(\boldsymbol u\cdot \boldsymbol w)-\boldsymbol w(\boldsymbol u\cdot \boldsymbol v) \end{aligned} \]

\(8.\quad\) 证明 \((\boldsymbol v\cdot\nabla)\boldsymbol v=(\nabla\times\boldsymbol v)\times \boldsymbol v+\dfrac12\nabla(\boldsymbol v^2)\)

\[\begin{aligned} (\nabla\times\boldsymbol v)\times \boldsymbol v=&\varepsilon_{klm}\varepsilon_{ijk}\partial_i \mathop{v_j}\limits^{\downarrow}v_l\boldsymbol e_m\\ =&(\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl})\partial_i \mathop{v_j}\limits^{\downarrow}v_l\boldsymbol e_m\\ =&\partial_i \mathop{v_j}\limits^{\downarrow}v_i\boldsymbol e_j-\partial_i \mathop{v_j}\limits^{\downarrow}v_j\boldsymbol e_i\\ =&(\boldsymbol v\cdot\nabla)\boldsymbol v-\frac12\partial_iv_j^2\boldsymbol e_i\\ =&(\boldsymbol v\cdot\nabla)\boldsymbol v-\frac12\nabla(\boldsymbol v^2) \end{aligned} \]

\(9.\quad\) 证明 \(\nabla\times(\boldsymbol u\times\boldsymbol v)=\boldsymbol u(\nabla\cdot\boldsymbol v)-\boldsymbol v(\nabla\cdot\boldsymbol u)+(\boldsymbol v\cdot \nabla)\boldsymbol u-(\boldsymbol u\cdot \nabla)\boldsymbol v\)

\[\begin{aligned} \nabla\times(\boldsymbol u\times\boldsymbol v)=&\varepsilon_{ijk}\partial_i\varepsilon_{mnj}\mathop{u_m}\limits^{\downarrow}\mathop{v_n}\limits^{\downarrow}\boldsymbol e_k\\ =&(\delta_{in}\delta_{km}-\delta_{im}\delta_{kn})\partial_i\mathop{u_m}\limits^{\downarrow}\mathop{v_n}\limits^{\downarrow}\boldsymbol e_k\\ =&\partial_i\mathop{u_k}\limits^{\downarrow}\mathop{v_i}\limits^{\downarrow}\boldsymbol e_k-\partial_i\mathop{u_i}\limits^{\downarrow}\mathop{v_k}\limits^{\downarrow}\boldsymbol e_k\\ =&u_k\partial_i\mathop{v_i}\limits^{\downarrow}\boldsymbol e_k+v_i\partial_i\mathop{u_k}\limits^{\downarrow}\boldsymbol e_k-u_i\partial_i\mathop{v_k}\limits^{\downarrow}\boldsymbol e_k-v_k\partial_i\mathop{u_i}\limits^{\downarrow}\boldsymbol e_k\\ =&\boldsymbol u(\nabla\cdot\boldsymbol v)+(\boldsymbol v\cdot \nabla)\boldsymbol u-(\boldsymbol u\cdot \nabla)\boldsymbol v-\boldsymbol v(\nabla\cdot\boldsymbol u) \end{aligned} \]

\(10.\quad\) 证明 \(\nabla(\boldsymbol u\cdot\boldsymbol v)=(\boldsymbol u\cdot\nabla)\boldsymbol v+(\boldsymbol v\cdot\nabla)\boldsymbol u+\boldsymbol u\times(\nabla\times\boldsymbol v)+\boldsymbol v\times(\nabla\times \boldsymbol u)\)

\[\begin{aligned} \mathbf{RHS}=&u_i\partial_i\mathop{v_j}\limits^{\downarrow}\boldsymbol e_j+v_i\partial_i\mathop{u_j}\limits^{\downarrow}\boldsymbol e_j+\varepsilon_{ijk}u_i\varepsilon_{mnj}\partial_m\mathop{v_n}\limits^{\downarrow}\boldsymbol e_k+\varepsilon_{ijk}v_i\varepsilon_{mnj}\partial_m\mathop{u_n}\limits^{\downarrow}\boldsymbol e_k\\ =&u_i\partial_i\mathop{v_j}\limits^{\downarrow}\boldsymbol e_j+v_i\partial_i\mathop{u_j}\limits^{\downarrow}\boldsymbol e_j+(\delta_{in}\delta_{km}-\delta_{im}\delta_{kn})u_i\partial_m\mathop{v_n}\limits^{\downarrow}\boldsymbol e_k\\ &+(\delta_{in}\delta_{km}-\delta_{im}\delta_{kn})v_i\partial_m\mathop{u_n}\limits^{\downarrow}\boldsymbol e_k\\ =&u_i\partial_i\mathop{v_j}\limits^{\downarrow}\boldsymbol e_j+v_i\partial_i\mathop{u_j}\limits^{\downarrow}\boldsymbol e_j+u_i\partial_k\mathop{v_i}\limits^{\downarrow}\boldsymbol e_k-u_i\partial_i\mathop{v_k}\limits^{\downarrow}\boldsymbol e_k\\&+v_i\partial_k\mathop{u_i}\limits^{\downarrow}\boldsymbol e_k-v_i\partial_i\mathop{u_k}\limits^{\downarrow}\boldsymbol e_k\\ =&u_i\partial_k\mathop{v_i}\limits^{\downarrow}\boldsymbol e_k+v_i\partial_k\mathop{u_i}\limits^{\downarrow}\boldsymbol e_k\\ =&\partial_k\mathop{u_i}\limits^{\downarrow}\mathop{v_i}\limits^{\downarrow}\boldsymbol e_k\\ =&\nabla(\boldsymbol u\cdot\boldsymbol v) \end{aligned} \]

\(11.\quad\) 证明 \(\nabla\times(\nabla\times\boldsymbol u)=\nabla(\nabla\cdot\boldsymbol u)-\nabla^2\boldsymbol u\)

\[\begin{aligned} \nabla\times(\nabla\times\boldsymbol u)=&\varepsilon_{ijk}\partial_i\varepsilon_{mnj}\partial_m\mathop{u_n}\limits^{\downarrow\downarrow}\boldsymbol e_k\\ =&(\delta_{in}\delta_{km}-\delta_{im}\delta_{kn})\partial_i\partial_m\mathop{u_n}\limits^{\downarrow\downarrow}\boldsymbol e_k\\ =&\partial_k\partial_i\mathop{u_i}\limits^{\downarrow\downarrow}\boldsymbol e_k-\partial_i\partial_i\mathop{u_k}\limits^{\downarrow\downarrow}\boldsymbol e_k\\ =&\nabla(\nabla\cdot\boldsymbol u)-\nabla^2\boldsymbol u \end{aligned} \]

\(12.\quad\) 计算三重积分 \(\displaystyle{\mathop{\iiint}\limits_V z\ \text dV,V=\Big\{(x,y,z)|x^2+y^2+\dfrac{z^2}{4}\leq1,z\geq0\Big\}}\)

耻辱题。大一下期末考试在这个题上白给了。
考虑椭球坐标变换

\[\begin{cases} x=\rho\sin\varphi\cos\theta\\ y=\rho\sin\varphi\sin\theta\\ z=2\rho\cos\varphi \end{cases} \]

雅可比行列式

\[|J|=\frac{\partial(x,y,z)}{\partial(\rho,\varphi,\theta)}=2\rho^2\sin\varphi \]

那么

\[\begin{aligned} \mathop{\iiint}\limits_V z\ \text dV=&\int_0^{2\pi}\text d\theta\int_0^\frac{\pi}{2}\text d\varphi\int_0^1 4\rho^3\sin\varphi\cos\varphi\text d\rho\\ =&2\pi\int_0^\frac{\pi}{2}\sin\varphi\cos\varphi\text d\varphi\\ =&\pi \end{aligned} \]

\(13.\quad\) 设 \(v_1,\cdots,v_m\) 是欧氏空间 \(V\) 的 \(m\) 个向量，\(G\) 是 Gram 矩阵，证明：
1）\(G\) 是半正定实对称矩阵；
2）\(v_1,\cdots,v_m\) 线性无关当且仅当 \(G\) 是正定阵，当且仅当 \(G\) 是可逆阵。

1）由欧氏空间内积的对称性可知 \(G\) 为实对称阵，任取 \(\alpha=(a_1,\cdots,a_m)'\in\mathbb R^m\)，令 \(v=a_1v_1+\cdots+a_mv_m\)，那么

\[\begin{aligned} \alpha'G\alpha=&\sum_{p=1}^m (\alpha'G)(1;p)\alpha_{p1}\\ =&\sum_{p=1}^m\sum_{q=1}^m \alpha'_{1q}g_{qp}\alpha_{p1}\\ =&\sum_{p=1}^m\sum_{q=1}^m a_pa_q(v_p,v_q)\\ =&(v,v)\\ \geq&0 \end{aligned} \]

2）由于 \(G\) 半正定，因此 \(G\) 正定当且仅当 \(G\) 可逆，只需证明一个。
充分性：设 \(G\) 正定，\(v=k_1v_1+\cdots+k_mv_m=0,\alpha=(k_1,\cdots,k_m)'\)，则
\(\alpha'G\alpha=(v,v)=0\)，由正定性的定义 \(\alpha=(k_1,\cdots,k_m)'=0\)，因此 \(v_1,\cdots,v_m\) 线性无关。
必要性：设 \(v_1,\cdots,v_m\) 线性无关，则 \(\forall \alpha=(\alpha_1,\cdots,a_m)'\ne 0,v\ne 0,\alpha'G\alpha=(v,v)>0\)，因此 \(G\) 正定。

\(14.\quad\) 设 \(V\) 是 \(n\) 维欧氏空间，\(\{e_1,\cdots,e_n\}\) 是一组基，\(c_1,\cdots,c_n\) 是 \(n\) 个实数，证明存在唯一 \(\alpha\in V\)，使得对任意 \(i\) 成立 \((\alpha,e_i)=c_i\)

设 \(\alpha=k_1e_1+\cdots+k_ne_n\)，则 \((\alpha,e_i)=k_1(e_1,e_i)+\cdots+k_n(e_n,e_i)\)，待证式等价于线性方程组

\[\begin{cases} (e_1,e_1)k_1+\cdots+(e_1,e_n)k_n=c_1\\ \cdots\\ (e_n,e_1)k_1+\cdots+(e_n,e_n)k_n=c_n \end{cases} \]

有唯一解。
考虑到系数矩阵是 Gram 阵，行列式大于 \(0\)，由 Cramer 法则知方程组有唯一解。

\(15.\quad\) 设 \(A\in M_n(\mathbb R)\) 是半正定实对称阵，证明 \(\forall x,y\in\mathbb R^n\)，成立

\[|x'Ay|^2\leq|x'Ax|\cdot|y'Ay| \]

由于 \(A\) 是半正定矩阵，所以存在实矩阵 \(C,A=C'C\)，由 Schwarz 不等式

\[|x'Ay|^2=|x'C'Cy|^2=|(Cx,Cy)|^2\leq||Cx||^2\cdot||Cy||^2=|x'Ax|\cdot|y'Ay| \]

\(16.\quad\) 证明 \(\displaystyle{\lim_{n\rightarrow\infty}\frac1n\int_0^\frac{\pi}{4}\arctan\left(\frac1x\right)\frac{\sin^2nx}{\sin^2x}\text dx=\frac{\pi^2}{4}}\)

考虑分段积分：

\[\int_0^\frac{\pi}{4}=\int_0^\frac{1}{\sqrt n}+\int_{\frac1{\sqrt n}}^{\frac{\pi}{4}} \]

\[\begin{aligned} \frac1n\int_0^\frac{1}{\sqrt n}\arctan\left(\frac1x\right)\frac{\sin^2nx}{\sin^2x}\text dx=&\arctan\left(\frac{1}{\xi}\right)\frac{\xi^2}{\sin^2\xi}\frac1n\int_0^\frac{1}{\sqrt n}\frac{\sin^2nx}{x^2}\text dx\\ \rightarrow&\frac{\pi}{2}\int_0^\infty \frac{\sin^2x}{x^2}\text dx\\ =&\frac{\pi^2}{4} \end{aligned} \]

其中注意 \(\xi\) 不一定和 \(\dfrac{1}{\sqrt n}\) 等价. 当然也可以用分点 \(\varepsilon\) 代替 \(\dfrac{1}{\sqrt n}\).

\[\begin{aligned} 0\leq&\frac1n\int_\frac{1}{\sqrt n}^\frac{\pi}{4}\arctan\left(\frac1x\right)\frac{\sin^2nx}{\sin^2x}\text dx\leq\frac1n\int_\frac{1}{\sqrt n}^\frac{\pi}{4}\frac\pi2\frac{1}{(\frac2\pi x)^2}\text dx\\ =&\frac{\pi^3}{8n}(-\frac{4}{\pi}+\sqrt n)\rightarrow0 \end{aligned} \]

因此

\[\lim_{n\rightarrow\infty}\frac1n\int_0^\frac{\pi}{4}\arctan\left(\frac1x\right)\frac{\sin^2nx}{\sin^2x}\text dx=\frac{\pi^2}{4} \]

另证：
由勒贝格控制收敛定理

\[\begin{aligned} &\lim_{n\rightarrow\infty}\frac1n\int_0^\frac{\pi}{4}\arctan\left(\frac1x\right)\frac{\sin^2nx}{\sin^2x}\text dx\\ =&\lim_{n\rightarrow\infty}\int_0^\frac{n\pi}{4}\frac{1}{n^2}\arctan\left(\frac{n}{x}\right)\frac{\sin^2x}{\sin^2\frac{x}{n}}\text dx\\ =&\int_0^\frac{n\pi}{4}\lim_{n\rightarrow\infty}\frac{1}{n^2}\arctan\left(\frac{n}{x}\right)\frac{\sin^2x}{\sin^2\frac{x}{n}}\text dx\\ =&\frac{\pi}{2}\int_0^\infty \frac{\sin^2x}{x^2}\text dx\\ =&\frac{\pi^2}{4} \end{aligned} \]

\(17.\quad\) \(f(x)\) 在 \([0,1]\) 连续，\(\displaystyle{\int_0^1 f(x)\text dx=0}\)，证明存在 \(\displaystyle{c\in(0,1),c^2f(c)=\int_0^c(x^2+x)f(x)\text dx}.\)

若 \(f(x)\equiv0\)，则命题显然成立。下证 \(f(x)\) 不恒为 \(0\) 的情况：
记

\[\begin{aligned} &f(c_1)=\mathop{\text{max}}\limits_{[0,1]}f(x)>0,f(c_2)=\mathop{\text{min}}\limits_{[0,1]}f(x)<0\ \ (c_1<c_2)\\&F(t)=t^2f(t)-\int_0^t (x^2+x)f(x)\text dx \end{aligned} \]

那么

\[\begin{aligned} F(c_1)\geq&c_1^2f(c_1)-f(c_1)\int_0^{c_1}(x^2+x)\text dx\\ =&(\frac{1}{2}c_1^2-\frac{1}{3}c_1^3)f(c_1)\\ > &0 \end{aligned} \]

同理 \(F(c_2)<0\)
由介值定理知存在 \(c\in(c_1,c_2),F(c)=0\)

\(18.\quad\) 设 \(f(x,y)\) 是 \(\mathbb R^2\) 上的连续可微函数，记 \(u(x,y)=-yf_x+xf_y\)，\(\displaystyle{I(\alpha)=\iint\limits_{D_\alpha}u(x,y)\text dx\text dy}\)，其中 \(D_\alpha:(x-2\cos\alpha)^2+(y-2\sin\alpha)^2\leq1\)，证明：\(I(\alpha)\) 必存在零点。

采用极坐标。
\(f_\varphi=-yf_x+xf_y=u(x,y)\)

\[\begin{aligned} \iint\limits_{D_\alpha}u(x,y)\text dx\text dy=&\iint\limits_{D_\alpha}f_\varphi\text dx\text dy\\ =&\int_1^3 \rho\text d\rho\int_{\alpha-\theta(\rho)}^{\alpha+\theta(\rho)}f_\varphi\text d\varphi\\ =&\int_1^3 \rho(f(\alpha+\theta(\rho))-f(\alpha-\theta(\rho)))\text d\rho \end{aligned} \]

接下来关于 \(\alpha\) 于 \([0,2\pi]\) 上积分：

\[\begin{aligned} \int_0^{2\pi} I(\alpha)\text d\alpha=&\int_0^{2\pi}\int_1^3 \rho(f(\alpha+\theta(\rho))-f(\alpha-\theta(\rho)))\text d\rho\text d\alpha\\ =&\int_1^3\rho\text d\rho\int_0^{2\pi}(f(\alpha+\theta(\rho))-f(\alpha-\theta(\rho)))\text d\alpha \end{aligned} \]

注意到

\[\int_0^{2\pi}(f(\alpha+\theta(\rho))-f(\alpha-\theta(\rho)))\text d\alpha=0 \]

因此

\[\int_0^{2\pi} I(\alpha)\text d\alpha=0 \]

亦即 \(I(\alpha)\) 存在零点。

\(19.\quad\) 证明：

1）\(\displaystyle{\lim_{n\rightarrow\infty}\sqrt[n]{n+1}=1}\)
2）设 \(\displaystyle{\lim_{n\rightarrow\infty}x_n=A,\lim_{n\rightarrow\infty}\frac{x_1+\cdots+x_n}{n}=A}\)

1）要证 \(|\sqrt[n]{n+1}-1|<\varepsilon\)，设 \(a=\sqrt[n]{n+1}-1\)，那么

\[1+n=(1+a)^n=1+na+\frac{n(n-1)}{2}a^2+\cdots\geq\frac{n(n-1)}{2}a^2 \]

\[0<a<\sqrt{\frac{2(n+1)}{n(n-1)}}\leq\frac{2}{\sqrt{n-1}}<\varepsilon \]

\[n>\frac4{\varepsilon^2}+1 \]

因此取 \(N=\dfrac4{\varepsilon^2}+1\) 即可。

2）分步法：

\[\left|\frac{(x_1-A)+\cdots+(x_n-A)}{n}\right|=\left|\frac{(x_1-A)+\cdots+(x_{N_1}-A)}{n}\right|+\left|\frac{(x_{N_1+1}-A)+\cdots+(x_n-A)}{n}\right| \]

其中 \(n>N_1\) 时 \(|x_n-A|<\dfrac{\varepsilon}{2}\)，\(n>N_2\) 时 \(\displaystyle{\left|\frac{(x_1-A)+\cdots+(x_{N_1}-A)}{n}\right|<\frac{\varepsilon}{2}}\)
取 \(N=\text{max}\{N_1,N_2\}\)，则上述两项分别小于 \(\dfrac{\varepsilon}{2}\)，因此

\[\left|\frac{(x_1-A)+\cdots+(x_n-A)}{n}\right|<\varepsilon \]

这告诉我们一个数列收敛，则前 \(n\) 项算术平均值也收敛于同一值。

\(20.\quad\) 证明：若 \(p_k>0\) 且

\[\lim_{n\rightarrow\infty}\frac{p_n}{p_1+\cdots+p_n}=0,\lim_{n\rightarrow\infty}a_n=a \]

则 \(\displaystyle{\lim_{n\rightarrow \infty}\frac{p_1a_n+\cdots+p_na_1}{p_1+\cdots+p_n}=a}\)

仍然采用分步法。

\[\begin{aligned} &\left| \frac{p_1a_n+\cdots+p_na_1}{p_1+\cdots+p_n}-a \right|\\\leq& \frac{1}{p_1+\cdots+p_n}(p_1|a_n-a|+\cdots+p_{n-N_1}|a_{N_1+1}-a|\\&+p_{n-N_1+1}M+\cdots+p_nM) \end{aligned} \]

存在 \(N_1\) 使得 \(n>N_1\) 时 \(\displaystyle{|a_n-a|<\frac{\varepsilon}{2}}\)
存在 \(N_2\) 使得 \(n>N_2\) 时 \(\displaystyle{\frac{p_n}{p_1+\cdots+p_n}<\frac{\varepsilon}{2MN_1}}\)
那么取 \(N=N_1+N_2\)，\(n>N\) 时

\[\begin{aligned} &\displaystyle{\frac{1}{p_1+\cdots+p_n}(p_1|a_n-a|+\cdots+p_{n-N_1}|a_{N_1+1}-a|)<\frac{\varepsilon}{2}}\\ &\displaystyle{\frac{1}{p_1+\cdots+p_n}(p_{n-N_1+1}M+\cdots+p_nM)<\frac{\varepsilon}{2}} \end{aligned} \]

因此

\[\lim_{n\rightarrow \infty}\frac{p_1a_n+\cdots+p_na_1}{p_1+\cdots+p_n}=a \]

\(21.\quad\) 证明：\(\displaystyle{\lim_{x\rightarrow1}\sqrt{\frac{7}{16x^2-9}}=1}\)

\[\begin{aligned} \left|\sqrt{\frac{7}{16x^2-9}}-1\right|=&\left|\frac{\dfrac{7}{16x^2-9}-1}{\sqrt{\dfrac{7}{16x^2-9}}+1}\right|\\ \leq&\left|\frac{7}{16x^2-9}-1\right|\\ =&\frac{16|1+x||1-x|}{|(4x+3)(4x-3)|}\\ \leq&32|x-1|,\ \ x\in U(1,\frac18)\\ \end{aligned} \]

取 \(\displaystyle{\delta=\text{min}\{\frac{\varepsilon}{32},\frac18\}}\) 即可。

\(22.\quad\) 设 \(x\rightarrow0\) 时，\(\displaystyle{f(x)\sim x,x_n=\sum_{i=1}^n f\left(\frac{2i-1}{n^2}a\right)}\)
证明：\(\displaystyle{\lim_{n\rightarrow\infty}x_n=a\ (a>0)}.\)

我们只需证明

\[\sum_{i=1}^n\left|f\left(\frac{2i-1}{n^2}a\right)-\frac{2i-1}{n^2}a\right|<\varepsilon \]

即

\[\left|f\left(\frac{2i-1}{n^2}a\right)-\frac{2i-1}{n^2}a\right|<\frac{2i-1}{n^2}\varepsilon \]

\[\left|\frac{f\left(\dfrac{2i-1}{n^2}a\right)}{\dfrac{2i-1}{n^2}a}-1\right|<\frac{\varepsilon}{a} \]

事实上由于 \(f(x)\sim x\ (x\rightarrow 0)\)

\[\left|\frac{f(x)}{x}-1\right|<\frac{\varepsilon}{a} \]

特别地，如果将 \(f(x)=\sin x\) 代入

\[\lim_{n\rightarrow\infty}\sum_{i=1}^n \sin\left(\frac{2i-1}{n^2}a\right)=a \]

这个题的本质是

\[\sum_{i=1}^n \frac{2i-1}{n^2}=1 \]

\(23.\quad\) 证明：
1）\(\displaystyle{\lim_{n\rightarrow\infty}\prod_{i=1}^n \left(1+\frac{2i-1}{n^2}a^2\right)=\text e^{a^2}}\)
2）\(\displaystyle{\lim_{n\rightarrow\infty}\prod_{i=1}^{n+1} \cos\left(\frac{\sqrt{2i-1}}{n}a^2\right)=\text e^{-\frac{a^4}{2}}}\)

1）

\[\begin{aligned} &\sum_{i=1}^n \ln\left(1+\frac{2i-1}{n^2}a^2\right)\\ \sim&\sum_{i=1}^n \frac{2i-1}{n^2}a^2\\ =&a^2\sum_{i=1}^n \frac{2i-1}{n^2}\\ =&a^2 \end{aligned} \]

因此

\[\lim_{n\rightarrow\infty}\prod_{i=1}^n \left(1+\frac{2i-1}{n^2}a^2\right)=\text e^{a^2} \]

2）

\[\begin{aligned} &\sum_{i=1}^{n+1} \ln\left(\cos\left(\frac{\sqrt{2i-1}}{n}a^2\right)\right)\\ \sim&-\frac{a^4}{2}\sum_{i=1}^{n+1} \frac{2i-1}{n^2}\\ \sim&-\frac{a^4}{2} \end{aligned} \]

因此

\[\lim_{n\rightarrow\infty}\prod_{i=1}^{n+1} \cos\left(\frac{\sqrt{2i-1}}{n}a^2\right)=\text e^{-\frac{a^4}{2}} \]

\(24.\quad\) 设 \(\displaystyle{\lim_{n\rightarrow\infty}a_n=a}\)，证明：

\[\lim_{n\rightarrow\infty}\frac{1}{2^n}\left(a_0+\binom{n}{1}a_1+\cdots+\binom{n}{k}a_k+\cdots+a_n\right)=a. \]

只需证明

\[\left|\frac{1}{2^n}\sum_{k=0}^n \binom{n}{k}a_k-a\right|<\varepsilon \]

取 \(k_0\) 使得 \(|a_k-a|<\dfrac{\varepsilon}{2}\)，那么上式小于

\[\sum_{k=0}^{k_0}\frac{n^k}{2^n}\cdot M+\frac{1}{2^n}\sum_{k=k_0+1}^n \binom{n}{k}\frac{\varepsilon}{2}<\frac{Mk_0n^{k_0}}{2}+\frac{\varepsilon}{2} \]

因 \(\displaystyle{\frac{Mk_0n^{k_0}}{2}\rightarrow0}\)，存在 \(N\) 使得 \(n>N\) 时 \(\displaystyle{\frac{Mk_0n^{k_0}}{2}<\frac{\varepsilon}{2}}\)
从而

\[\lim_{n\rightarrow\infty}\frac{1}{2^n}\left(a_0+\binom{n}{1}a_1+\cdots+\binom{n}{k}a_k+\cdots+a_n\right)=a. \]

\(25.\quad\) 设 \(x_n=\dfrac{\sin1}{2}+\cdots+\dfrac{\sin n}{2^n}\)，证明 \(\{x_n\}\) 收敛.

由柯西收敛准则

\[\begin{aligned} |x_{n+p}-x_n|\leq&\frac{1}{2^{n+1}}+\cdots+\frac{1}{2^{n+p}}\\ =&\frac{1}{2^{n+1}}\left(1+\frac{1}{2}+\cdots+\frac{1}{2^{p-1}}\right)\\ \leq&\frac{1}{2^{n+1}}\left(\frac{1}{1-\frac12}\right)\\ =&\frac{1}{2^n}\\ <&\frac1n \end{aligned} \]

取 \(N=\dfrac{1}{\varepsilon}\)，则当 \(n>N\) 时 \(|x_{n+p}-x_n|<\varepsilon\)

\(26.\quad\) 证明数列 \(x_n=1+\dfrac12+\cdots+\dfrac1n-\ln n\) 单调下降有界.

先证明单调递减，考虑

\[\ln n-\ln (n-1)=\frac{1}{\xi}>\frac{1}{n} \]

累加得

\[a_n<a_{n-1} \]

再证明有下界，考虑

\[\ln n-\ln (n-1)=\frac{1}{\xi}<\frac{1}{n-1} \]

因此

\[\begin{aligned} x_n=&1+\frac12+\cdots+\frac{1}{n}-\ln n\\ >&\ln2-\ln1+\ln3-\ln2+\cdots+\ln n-\ln(n-1)+\frac1n-\ln n\\ =&\frac{1}{n}\\ >&0 \end{aligned} \]

由单调有界原理知极限存在.

\(27.\quad\) 设函数 \(f(x)\) 在点 \(x_0\) 的邻域 \(I\) (点 \(x_0\) 可能例外) 内有定义. 证明：如果对于任意点列 \(\{x_n\}\). 这里 \(x_n\in I,x_n\rightarrow x_0(n\rightarrow\infty),0<|x_{n+1}-x_0|<|x_n-x_0|\)，都有 \(\displaystyle{\lim_{n\rightarrow\infty}f(x_n)=A}\)，那么
\(\displaystyle{\lim_{x\rightarrow x_0}f(x)=A}\)

采用反证法：
若 \(f(x)\) 不趋于 \(A\)，则 \(\exists \varepsilon_0>0,\forall \delta>0,\exists x_\delta\in I\)，虽然 \(0<|x_\delta-x_0|<\delta\)，但是 \(|f(x_\delta)-A|\geq\varepsilon_0\)
取 \(\delta_1=1,|f(x_1)-A|\geq\varepsilon_0\)
取 \(\displaystyle{\delta_2=\text{min}\left\{\frac12,|x_1-x_0|\right\},|f(x_2)-A|\geq\varepsilon_0}\)（为了符合 \(0<|x_{n+1}-x_0|<|x_n-x_0|\) 的要求）
取 \(\displaystyle{\delta_3=\text{min}\left\{\frac13,|x_2-x_0|\right\}\cdots}\)

无限进行下去可得点列 \(\{x_n\},x_n\in I,x_n\rightarrow x_0,0<|x_{n+1}-x_0|<|x_n-x_0|\)，但

\[|f(x_n)-A|\geq\varepsilon_0 \]

这与 \(\displaystyle{\lim_{n\rightarrow\infty}f(x_n)=A}\) 矛盾.

\(28.\quad\) 证明从任一数列 \(\{x_n\}\) 中必可选出一个（不一定严格）单调的子数列.

假若 \(\{x_n\}\) 中存在递增子序列，则问题已被解决. 若 \(\{x_n\}\) 中无递增子序列，则存在 \(n_1>0,\forall n>n_1,x_n<x_{n_1}\)（因为无法取到 \(n_1\) 仅可能于存在递增子序列时）
同样在 \(\{x_n\}_{n>n_1}\) 中也无递增子序列，同样取出 \(n_2\cdots\)

无限进行下去可得严格递减子序列 \(\{x_{n_k}\}\)

\(29.\quad\) 证明

\[1^3+2^3+\cdots+n^3=(1+2+\cdots+n)^2 \]

数学归纳法：
\(n=1\) 时等式成立. 设 \(n=k\) 时成立，\(n=k+1\) 时

\[\begin{aligned} 1^3+2^3+\cdots+(k+1)^3=&(1+2+\cdots+k)^2+(k+1)^3\\ (1+2+\cdots+k+1)^2=&(1+2+\cdots+k)^2+2(1+2+\cdots+k)(k+1)+(k+1)^2\\ =&(1+2+\cdots+k)^2+(k+1)^3 \end{aligned} \]

因此

\[1^3+2^3+\cdots+(k+1)^3=(1+2+\cdots+k+1)^2 \]

命题得证.

\(30.\quad\) 证明

\[\lim_{x\rightarrow0}\left[\frac{a_1^x+\cdots+a_n^x}{n}\right]^\frac{1}{x}=\sqrt[n]{a_1\cdots a_n} \]

考虑对数

\[\begin{aligned} &\frac{1}{x}\ln\left(\frac{a_1^x+\cdots+a_n^x}{n}\right)\\ \sim&\frac{1}{x}\left[\frac{(a_1^x-1)+\cdots+(a_n^x-1)}{n}\right]\\ =&\frac{1}{n}\left(\frac{a_1^x-1}{x}+\cdots+\frac{a_n^x-1}{x}\right)\\ \sim&\frac{1}{n}\ln(a_1\cdots a_n) \end{aligned} \]

因此

\[\lim_{x\rightarrow0}\left[\frac{a_1^x+\cdots+a_n^x}{n}\right]^\frac{1}{x}=\sqrt[n]{a_1\cdots a_n} \]

<新知识>

伯努利数：定义

\[\frac{x}{\text e^x-1}=\sum_{n=0}^\infty \frac{\varphi_n}{n!}x^n \]

可以通过掩盖法计算每一个伯努利数：

\[\varphi_n=\frac{\text d^n}{\text dx^n}\left(\frac{x}{\text e^x-1}\right)\bigg|_{x=0} \]

\[\varphi_0=1,\varphi_1=-\dfrac{1}{2},\varphi_2=\dfrac{1}{6},\cdots \]

伯努利多项式：定义

\[\frac{x\text e^{xt}}{\text e^x-1}=\sum_{n=0}^\infty \frac{x^n}{n!}\varphi_n(t) \]

注意到

\[\varphi_n(0)=\varphi_n \]

根据定义

\[\begin{aligned} &\frac{x}{\text e^x-1}\cdot\text e^{xt}\\ =&\sum_{n=0}^\infty \frac{\varphi_n x^n}{n!}\cdot\sum_{k=0}^\infty \frac{(xt)^k}{k!}\\ =&\sum_{n=0}^\infty \sum_{k=0}^n \frac{\varphi_k x^k}{k!}\frac{(xt)^{n-k}}{(n-k)!}\\ =&\sum_{n=0}^\infty \frac{x^n}{n!} \sum_{k=0}^n \binom{n}{k} \varphi_k t^{n-k} \end{aligned} \]

比较得 \(\varphi_n(x)\) 的显明表达式

\[\varphi_n(x)=\sum_{k=0}^n \binom{n}{k}\varphi_k x^{n-k} \]

简记为

\[\varphi_n(x)=(\varphi+x)^n \]

同样根据定义

\[\begin{aligned} 1=&\frac{\text e^x-1}{x}\cdot \sum_{k=0}^\infty \frac{\varphi_k}{k!}x^k\\ =&\sum_{n=1}^\infty \frac{x^{n-1}}{n!}\sum_{k=0}^\infty \frac{\varphi_k}{k!}x^k\\ =&\sum_{n=1}^\infty x^{n-1} \sum_{k=0}^{n-1} \frac{1}{(n-k)!}\frac{\varphi_k}{k!} \end{aligned} \]

比较对应系数 \(\displaystyle{\sum_{k=0}^{n-1} \frac{1}{(n-k)!}\frac{\varphi_k}{k!}=0}\)
亦即

\[\sum_{k=0}^{n-1}\binom{n}{k}\varphi_k=0 \]

简记为

\[\varphi_n=(\varphi+1)^n \]

伯努利多项式的差分关系常用于计算等幂和

\[\varphi_n(x+1)=\varphi_n(x)+nx^{n-1} \]

这同样通过定义展开证明. 它告诉我们幂等于伯努利多项式的差分.
因此

\[s^n=\frac{1}{n+1}[\varphi_{n+1}(s+1)-\varphi_{n+1}(s)] \]

累加得

\[\sum_{s=1}^m s^n=\frac{1}{n+1}[\varphi_{n+1}(m+1)-\varphi_{n+1}] \]

类比伯努利多项式，定义欧拉多项式

\[\frac{2\text e^{xt}}{\text e^x+1}=\sum_{n=0}^\infty \frac{x^n}{n!}\text E_n(t) \]

令 \(t=\dfrac12\)

\[\frac{2\text e^{\frac{x}{2}}}{\text e^x+1}=\text{sech}\frac{x}{2}=\sum_{n=0}^\infty \frac{(-)^n\text E_n}{(2n)!}\left(\frac{x}{2}\right)^{2n} \]

其中欧拉数

\[\text E_n=(-)^n2^{2n} \text E_{2n}\left(\frac12\right) \]

可以证明，幂等于欧拉多项式的均值

\[\text E_{n}(x+1)+\text E_{n}(x)=2x^n \]

累加得

\[\sum_{s=1}^m (-)^ss^n=\frac12[(-)^m\text E_{n}(m+1)-\text E_n(1)] \]

差分方程与微分方程：它们本质是相同的。
考虑

\[a_{n+2}+pa_{n+1}+qa_n=0 \]

设 \(\displaystyle{y=a_0+a_1t+\cdots+\frac{a_n}{n!}t^n+\cdots}\)
则 \(\displaystyle{D^{n+2}y(0)+pD^{n+1}y(0)+qD^n y(0)=0}\)
解 \(y''+py'+qy=0\) 求 \(n\) 次导并代入 \(x=0\) 就可以了.
如果 \(\displaystyle{y=C_1\text e^{\lambda_1x}+C_2\text e^{\lambda_2x}}\)
那么 \(\displaystyle{a_n=D^n y(0)=C_1\lambda_1^n+C_2\lambda_2^n}\)

\(31.\quad\) 若 \(\displaystyle{\lim_{n\rightarrow\infty}x_n=a,\lim_{n\rightarrow\infty}y_n=b}\)，证明

\[\lim_{n\rightarrow\infty}\frac{x_1y_n+\cdots+x_ny_1}{n}=ab. \]

令 \(x_n=a+\alpha_n,y_n=b+\beta_n\)，则 \(n\rightarrow\infty\) 时 \(\alpha_n,\beta_n\rightarrow0\)

\[\begin{aligned} &\frac{x_1y_n+\cdots+x_ny_1}{n}\\ =&\frac{(a+\alpha_1)(b+\beta_n)+\cdots+(a+\alpha_n)(b+\beta_1)}{n}\\ =&ab+a\frac{\beta_1+\cdots+\beta_n}{n}+b\frac{\alpha_1+\cdots+\alpha_n}{n}+\frac{\alpha_1\beta_n+\cdots+\alpha_n\beta_1}{n} \end{aligned} \]

由于算术均值的极限等于原数列的极限，后三项趋于 \(0\)，因此

\[\lim_{n\rightarrow\infty}\frac{x_1y_n+\cdots+x_ny_1}{n}=ab \]

\(32.\quad\) 求极限 \(\displaystyle{\lim_{n\rightarrow\infty}x_n}\)，设

\[\begin{aligned} &x_n=\frac{1\cdot3\cdots(2n-1)}{2\cdot4\cdots(2n)}\\ &x_n=\sum_{k=n^2}^{(n+1)^2}\frac{1}{\sqrt k}\\ &x_n=\sum_{k=1}^n [(n^k+1)^{-\frac{1}{k}}+(n^k-1)^{-\frac1k}]\\ &x_n=(n!)^{\frac{1}{n^2}} \end{aligned} \]

1）考虑 AM-GM

\[2n=\frac{(2n-1)+(2n+1)}{2}>\sqrt{(2n-1)(2n+1)} \]

由此

\[0<x_n=\frac{1\cdot3\cdots(2n-1)}{2\cdot4\cdots(2n)}<\frac{1}{\sqrt{2n+1}}\rightarrow0 \]

2）\(\displaystyle{\sum_{k=n^2}^{(n+1)^2}\frac{1}{\sqrt k}}\) 一共有 \(2n+2\) 项，最小项为 \(\dfrac{1}{n+1}\)，最大项为 \(\frac1n\)

\[\frac{2n+2}{n+1}\leq\sum_{k=n^2}^{(n+1)^2}\frac{1}{\sqrt k}\leq\frac{2n+2}{n} \]

左右两端极限皆为 \(2\)

3）因 \(n^k<n^k+1<(n+1)^k\)，所以 \(n^{-1}>(n^k+1)^{-\frac1k}>(n+1)^{-1}\)

\[\frac{n}{n}>\sum_{k=1}^n(n^k+1)^{-\frac1k}>\frac{n}{n+1} \]

由夹逼定理 \(\displaystyle{\lim_{n\rightarrow\infty}\sum_{k=1}^n(n^k+1)^{-\frac1k}=1}\)，同理 \(\displaystyle{\lim_{n\rightarrow\infty}\sum_{k=1}^n(n^k-1)^{-\frac1k}=1}\)
从而

\[\lim_{n\rightarrow\infty}x_n=2 \]

4）考虑 \(1\leq(n!)^{\frac{1}{n!}}\leq(n^n)^{\frac{1}{n^2}}=n^{\frac{1}{n}}\)
因为 \(n^{\frac{1}{n}}\rightarrow 1\)，所以 \(\displaystyle{\lim_{n\rightarrow\infty}x_n=1}\)

\(33.\quad\) 设 \(f(x)>0\)，在区间 \([0,1]\) 上连续，证明：

\[\lim_{n\rightarrow\infty}\sqrt[n]{\sum_{i=1}^n\left(f\left(\frac{i}{n}\right)\right)^n\frac1n}=\mathop{\text{max}}\limits_{0\leq x\leq 1}f(x) \]

记 \(M=\mathop{\text{max}}\limits_{0\leq x\leq 1}f(x)\)，显然 \(x_n\leq M\)，下面考虑下界：
设 \(f(x_0)=M\)，那么 \(\forall \varepsilon>0,\exists \delta>0\)，当 \(|x-x_0|<\delta\) 时 \(M-\varepsilon<f(x)<M+\varepsilon\)
当 \(n\) 充分大时 \(\dfrac1n<\delta\)，存在 \(i_0\) 使得

\[f\left(\frac{i_0}{n}\right)>M-\varepsilon \]

因此

\[x_n\geq\sqrt[n]{\left(f\left(\frac{i_0}{n}\right)\right)^n\frac1n}>(M-\varepsilon)\frac{1}{\sqrt[n]{n}} \]

即

\[(M-\varepsilon)\frac{1}{\sqrt[n]{n}}\leq x_n\leq M \]

命题得证.

这一题告诉我们 \(f(x)>0\) 时

\[\lim_{n\rightarrow\infty}\sqrt[n]{\int_0^1 (f(x))^n\text dx}=\mathop{\text{max}}\limits_{0\leq x\leq 1}f(x) \]

\(34.\quad\) 求 \(\displaystyle{\lim_{n\rightarrow\infty}\left[\frac{1}{n^2}+\cdots+\frac{1}{(2n)^2}\right]}\)

由于级数 \(\displaystyle{\sum_{k=1}^\infty \frac{1}{k^2}}\) 收敛，其余项

\[R_n=\sum_{k=n+1}^\infty \frac{1}{k^2}\rightarrow 0 \]

\[0\leq \frac{1}{n^2}+\cdots+\frac{1}{(2n)^2}\leq R_{n-1}\rightarrow0 \]

故原极限为 \(0.\)
本质上是柯西收敛准则.

\(35.\quad\) 设 \(x_n=\dfrac{1}{2\ln2}+\cdots+\dfrac{1}{n\ln n}-\ln\ln n\)，证明 \(\{x_n\}\) 收敛.

考虑差分

\[|x_{n+1}-x_n|=\left|\frac{1}{(n+1)\ln(n+1)}-\frac{1}{\xi_n\ln\xi_n}\right|\leq\frac{1}{n\ln n}-\frac{1}{(n+1)\ln(n+1)} \]

因此

\[\sum_{k=2}^\infty |x_{k+1}-x_k|\leq\frac{1}{2\ln2} \]

差分数列是收敛的，原数列也是收敛的.

\(36.\quad\) 设函数 \(f(x)\) 是周期为 \(T\) 的连续周期函数. 证明

\[\lim_{x\rightarrow+\infty}\frac{1}{x}\int_0^x f(t)\text dt=\frac{1}{T}\int_0^T f(t)\text dt \]

考虑夹逼定理：

\[\frac{1}{(n+1)T}\int_0^{nT} f(t)\text dt\leq \frac{1}{x}\int_0^x f(t)\text dt\leq\frac{1}{nT}\int_0^{(n+1)T}f(t)\text dt \]

两端都趋于 \(\displaystyle{\frac{1}{T}\int_0^T f(t)\text dt}\)

\(37.\quad\) 设 \(f'(x)\) 是 \([0,+\infty)\) 上的连续函数，\(\displaystyle{\lim_{x\rightarrow+\infty}[f(x)+f'(x)]=0}\)，证明

\[\lim_{x\rightarrow+\infty}f(x)=0. \]

考虑 \((\text e^x f(x))'=\text e^xf(x)+\text e^xf'(x)\)
两端在 \([a,x]\) 积分

\[\text e^xf(x)=\text e^af(a)+\int_a^x \text e^x[f(x)+f'(x)]\text dx \]

\[|f(x)|\leq \frac{\text e^a}{\text e^x}|f(a)|+\frac{1}{\text e^x}\int_a^x \text e^x|f(x)+f'(x)|\text dx \]

令 \(\left|\dfrac{\text e^a}{\text e^x}f(a)\right|<\dfrac{\varepsilon}{2},|f(x)+f'(x)|<\dfrac{\varepsilon}{2}\)，那么

\[|f(x)|<\varepsilon \]

命题得证.

\(38.\quad\) 证明韦达公式：

\[\frac{2}{\pi}=\sqrt{\frac12}\cdot\sqrt{\frac12+\frac12\sqrt{\frac12}}\cdot\sqrt{\frac12+\frac12\sqrt{\frac12+\frac12\sqrt{\frac12}}}\cdots \]

上式可改写为

\[\frac2\pi=x_1x_2\cdots x_n,\quad x_{n+1}=\sqrt{\frac{1+x_n}{2}},x_1=\sqrt{\frac12} \]

而

\[\cos\frac{\pi}{4}\cdots \cos\frac{\pi}{2^{n+1}}=\frac{1}{\sin\frac{\pi}{2^{n+1}}}\cdot\frac{1}{2^n}=\frac2\pi \]

证讫.

\(39.\quad\) 设极限 \(\displaystyle{\lim_{n\rightarrow\infty}(a_1+\cdots+a_n)}\) 存在，求：
1）\(\displaystyle{\lim_{n\rightarrow \infty}\dfrac{1}{n}(a_1+2a_2+\cdots+na_n)}\);
2）\(\displaystyle{\lim_{n\rightarrow \infty}(n!a_1\cdots a_n)^\frac1n}.\)

1）记 \(\displaystyle{S_n=\sum_{k=1}^n a_k}\)，考虑阿贝尔变换：

\[\begin{aligned} \frac1n \sum_{k=1}^n ka_k=&S_n-\sum_{k=1}^{n-1}S_k\Delta k\\ =&S_n-\sum_{k=1}^{n-1}S_k \end{aligned} \]

由于数列极限等同于算术均值的极限，上式趋于 \(0\).
2）利用 \(0\leq(1a_1\cdots na_n)^{\frac1n}\leq\dfrac{a_1+2a_2+\cdots+na_n}{n}\) 即可.

\(40.\quad\) \(x_n>0,\displaystyle{\lim_{n\rightarrow\infty}x_n=0}\)，证明：

\[\lim_{n\rightarrow\infty}\mathop{\text{sup}}\limits_{k\geq1}\left(\prod_{i=1}^n x_{i+k}\right)^{\frac1n}=0 \]

注意到

\[\mathop{\text{sup}}\limits_{k\geq1}\left(\prod_{i=1}^n x_{i+k}\right)^{\frac{1}{n}} \leq\left(\prod_{i=1}^n\mathop{\text{sup}}\limits_{k\geq1} x_{i+k}\right)^\frac1n \]

令 \(b_i=\mathop{\text{sup}}\limits_{k\geq1} x_{i+k}\)，则 \(b_i\rightarrow0\)，由 AM-GM 不等式即证.

\(41.\quad\) 设 \(f\) 是 \(\mathbb R\) 上的可微函数，\(\displaystyle{\lim_{x\rightarrow+\infty}f'(x)=A>0}\)，证明

\[\lim_{x\rightarrow+\infty}f(x)=+\infty \]

反证之.
若 \(f\) 趋于 \(C\),即 \(\displaystyle{\lim_{x\rightarrow+\infty}f(x)=C}\)
存在 \(x>M,|f(x)-C|<\varepsilon\)
而 \(\displaystyle{\lim_{x\rightarrow+\infty}f'(x)=A}\) 得 \(x>M_1,f'(x)>A-\varepsilon\)
取 \(x_1,x_2>\text{max}\{M,M_1\},x_2-x_1>\dfrac{2\varepsilon}{A-\varepsilon}\)
产生矛盾.

\(42.\quad\) 1）若存在常数 \(r(0<r<1),|x_{n+1}-x_n|\leq r|x_n-x_{n-1}|\)，证明 \(\{x_n\}\) 收敛；
2）\(x_{n+1}=f(x_n),|f'(x)\leq r<1|\)，证明 \(\{x_n\}\) 收敛.

1）

\[\begin{aligned} |x_{n+p}-x_n|\leq&\sum_{k=n+1}^{n+p}|x_k-x_{k-1}|\\ \leq& \sum_{k=n+1}^{n+p} r^{k-1}|x_1-x_0|\\ =&|x_1-x_0|\cdot\frac{r^n-r^{n+p}}{1-r}\\ \leq&|x_1-x_0|\frac{r^n}{1-r} \end{aligned} \]

由柯西准则知收敛.

2）利用微分中值

\[\begin{aligned} |x_{n+1}-x_n|=&|f(x_n)-f(x_{n-1})|\\ =&|f'(\xi)(x_N-x_{n-1})|\\ \leq& r|x_n-x_{n-1}| \end{aligned} \]

后续证明同上.

此题称作“压缩映像原理”，\(f\) 是压缩映射，\(r\) 是压缩常数.

\(43.\quad\) 已知 \(x_{n+1}=f(x_n)\)，\(f\) 是增函数，若存在不动点 \(x^*=f(x^*)\) 满足

\[(x_1-f(x_1))(x_1-x^*)\geq0 \]

则数列 \(\{x_n\}\) 必收敛.

对 \(x_1\) 分类：只证明 \(x_1>x^*\) 的情况，其余同理.
一方面，\(x_{n+1}=f(x_n)\geq f(x^*)=x^*\)（数学归纳法），这样 \(x^*\) 是下界；
另一方面，\(x_{n+1}=f(x_n)\leq f(x_{n-1})=x_n\)（数学归纳法），这样 \(x_n\) 递减.
由单调有界原理，数列 \(\{x_n\}\) 收敛.

此题称作“不动点方法”.
注意 \(f\) 必须是增函数，减函数不成立.

\(44.\quad\) 证明：若 \(f\) 在 \(I\equiv [a-r,a+r]\) 上可微，

\[|f'(x)\leq \alpha<1,|f(a)-a|\leq (1-\alpha)r \]

任取 \(x_0\in I,x_1=f(x_0),\cdots,x_n=f(x_{n-1})\)，则 \(\displaystyle{\lim_{n\rightarrow\infty}x_n=x^*}\)（\(x^*\) 为不动点）

先证明一切 \(x_n\in I\):

\[\begin{aligned} |x_{n+1}-a|=&|f(x_n)-f(a)+f(a)-a|\\ \leq& |f'(\xi)||x_n-a|+|f(a)-a|\\ \leq& \alpha r+(1-\alpha)r\\ =&r \end{aligned} \]

再证明收敛：

\[|x_{n+1}-x_n|=|f'(\xi)(x_n-x_{n-1})|\leq \alpha|x_n-x_{n-1}| \]

那么 \(f\) 是一个压缩映射，数列必然收敛. 考虑到在 \(x_n=f(x_{n-1})\) 取极限即为 \(x=f(x)\) 的根.

\(45.\quad\) 设 \(f\) 映 \([a,b]\) 到自身，且

\[|f(x)-f(y)|\leq |x-y| \]

任取 \(x_1\in[a,b]\)，令

\[x_{n+1}=\frac12[x_n+f(x_n)] \]

求证数列有极限 \(x^*\)，\(x^*\) 满足方程 \(f(x^*)=x^*\).

题设已经告诉有界了，只要能证明 \(\{x_n\}\) 单调就可以了. 不妨设 \(x_1\leq f(x_1)\).
数学归纳：

\[x_2=\frac12[x_1+f(x_1)]\geq x_1 \]

\[f(x_{n-1})-f(x_n)\leq |f(x_{n-1})-f(x_n)|\leq |x_{n-1}-x_n|=x_n-x_{n-1} \]

因此

\[x_n=\frac12[x_{n-1}+f(x_{n-1})]\leq \frac12[x_n+f(x_n)]=x_{n+1} \]

故 \(\{x_n\}\) 单调递增.

\(46.\quad\) 证明数列

\[2,2+\frac12,2+\frac{1}{2+\dfrac12},\cdots \]

收敛，并求其极限.

极限是好求的：

\[A=2+\frac1A,A=1+\sqrt2 \]

考虑到

\[|x_{n+1}-x_n|=\left|\frac{1}{x_n}-\frac{1}{x_{n-1}}\right|=\frac{|x_{n-1}-x_n|}{|x_n x_{n-1}|}\leq\frac14|x_n-x_{n-1}| \]

是一个压缩映射，数列是收敛的.

\(47.\quad\) 已知 \(z=f(x,y)\) 为 \(x>0,y>0\) 上定义的正连续函数，\(z\) 分别对 \(x,y\) 单增，若:（1）存在点 \(b\) 是 \(f(x,x)\) 的不动点;（2）当且仅当 \(x>b\) 时 \(x>f(x,x).\) 令 \(a_1=f(a,a),a_2=f(x_1,a),a_n=f(a_{n-1},a_{n-2})\)，证明 \(\{a_n\}\) 单调有界存在极限，且极限为不动点.

只证 \(a\leq a_1\) 的情况：

\[a_2=f(a_1,a)\geq f(a,a)=a_1,a_3=f(a_2,a_1)\geq f(a_1,a_1)\geq f(a_1,a)=a_2 \]

\[a_{n+1}=f(a_n,a_{n-1})\geq f(a_{n-1},a_{n-2})=a_n \]

因此 \(\{a_n\}\) 单增.
考虑到 \(a\leq b\)

\[a_1=f(a,a)\leq f(b,b)=b,a_2=f(a_1,a)\leq f(b,a)\leq f(b,b)=b \]

由数学归纳法知 \(a_n\leq b\).
命题得证.

\(48.\quad\) \(a>0,a_1=(a+a^\frac13)^\frac13,a_2=(a_1+a^\frac13)^\frac13,\cdots,a_n=(a_{n-1}+a_{n-2}^\frac13)^\frac13\)，证明:
1）数列 \(\{a_n\}\) 为单调有界数列;
2）数列 \(\{a_n\}\) 收敛于 \(x^3=x+x^\frac13\) 的一个正根.

仿照上题, 不妨设 \(a\leq a_1:\)
考虑到 \(z=(x+y^\frac13)^\frac13\) 关于 \(x,y\) 递增, 可证 \(a_{n-1}\leq a_n\) 单增有上界;
继续考虑 \(x^3-x-x^\frac13\) 给定范围内只有一个根即不动点即可.

\(49.\quad\) 对于数列 \(x_0=a,0<a<\dfrac\pi2,x_n=\sin x_{n-1}\), 证明

\[\lim_{n\rightarrow\infty}\sqrt{\frac{n}{3}}x_n=1. \]

原题等价于证明

\[\lim_{n\rightarrow\infty}\frac{n}{\frac{1}{x_n^2}}=3 \]

由 Stolz 公式

\[\begin{aligned} \lim_{n\rightarrow\infty}\frac{n}{\frac{1}{x_n^2}}=&\lim_{n\rightarrow\infty}\frac{n-(n-1)}{\frac{1}{x_n^2}-\frac{1}{x_{n-1}^2}}\\ =&\lim_{n\rightarrow\infty}\frac{1}{\frac{1}{\sin^2 x_{n-1}}-\frac{1}{x_{n-1}^2}}\\ =&\lim_{x\rightarrow 0}\frac{x^2\sin^2x}{x^2-\sin^2x}\\ =&\lim_{x\rightarrow0}\frac{x^4}{(2x+o(x))(\frac16 x^3+o(x^3))}\\ =&3 \end{aligned} \]

\(50.\quad\) 证明：

\[\lim_{n\rightarrow\infty}\frac{\displaystyle{\sum_{k=1}^n} (-1)^k \binom{n}{k}\ln k}{\ln(\ln k)}=1. \]

\[\begin{aligned} \sum_{k=1}^n (-1)^k \binom{n}{k} \ln k=&\sum_{k=1}^n (-1)^k\left(\binom{n-1}{k}+\binom{n-1}{k-1} \right)\ln k\\ =&\sum_{k=1}^{n-1} \binom{n-1}{k}+\sum_{k=1}^n (-1)^k\binom{n-1}{k-1}\ln k\\ =&\sum_{k=1}^{n-1} \binom{n-1}{k}+\sum_{k=1}^{n-1} (-1)^{k+1}\binom{n-1}{k}\ln(k+1)\\ =&\sum_{k=1}^{n-1} (-1)^k\binom{n-1}{k}(\ln k-\ln(k+1))\\ =&(-1)^{k+1}\sum_{k=1}^{n-1} \binom{n-1}{k} \int_0^1 \frac{1}{x+k} \text dx\\ =&(-1)^{k+1}\int_0^1\int_0^1\sum_{k=1}^{n-1} \binom{n-1}{k} u^{x+k-1} \text du \text dx\\ =&-\int_0^1\int_0^1 u^{x-1}[(1-u)^{n-1}-1]\text du\text dx\\ =&-\int_0^1\left(\frac{\Gamma(x)\Gamma(n)}{\Gamma(x+n)}-\frac1x\right)\text dx\\ =&\int_0^1 \frac1x\left(1-\frac{(n-1)!}{(x+1)\cdots(x+n-1)}\right)\text dx\\ =&\int_0^1 \frac1x\left(1-\text e^{(-\ln n+C)x}\right)\text dx\quad\quad (*) \end{aligned} \]

令 \(a_n=\ln n+C\)，则

\[\begin{aligned} \int_0^1 \frac1x(1-\text e^{-a_nx})\text dx=&\int_0^{a_n} \frac1x(1-\text e^{-x})\text dx\\ =&\int_0^1 \frac1x(1-\text e^{-x})\text dx+\int_1^{a_n}\frac{1}{x}(1-\text e^{-x})\text dx\\ =&\ln a_n+\int_0^1 \frac1x(1-\text e^{-x})\text dx-\int_1^{a_n}\frac{\text e^{-x}}{x}\text dx\\ =&\ln a_n+O(1) \end{aligned} \]

关于 \((*)\) 式的说明：

\[\begin{aligned} &\frac{(n-1)!}{(x+1)\cdots(x+n-1)}\\ =&\prod_{k=1}^{n-1} (1+\frac{x}{k})^{-1}\\ =&\text{exp}\left\{-\displaystyle{\sum_{k=1}^{n-1}\ln(1+\frac{x}{k})}\right\} \end{aligned} \]

对 \(\ln\) 幂级数展开：

\[\begin{aligned} &\sum_{k=1}^{n-1}\ln(1+\frac{x}{k})\\ =&\sum_{k=1}^{n-1} \frac{x}{k}+O(\sum_{k=1}^{n-1}\frac{x^2}{k^2})\\ =&x(\ln n+\gamma)+O(x^2) \end{aligned} \]

那么

\[\frac{(n-1)!}{(x+1)\cdots(x+n-1)}=\text e^{-(\ln n+\gamma)x}\text e^{O(x^2)}=\text e^{-(\ln n+\gamma)x}+O(x^2\text e^{-(\ln n+\gamma)x}) \]

其中

\[O(\int_0^1 x\text e^{-(\ln n+\gamma)x}\text dx)=O(\frac{1}{\ln^2n}) \]

被省略了.

\(51.\quad\) 证明：
1）\(\displaystyle{\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}}\);
2）\(\displaystyle{\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}}\);
3）\(\displaystyle{\binom{n}{k}=\frac{n}{n-k}\binom{n-1}{k}}\).

1）考虑 \(n\) 个物体中挑选 \(k\) 个，选择 \(n_i\) 的方案有 \(\displaystyle\binom{n-1}{k-1}\) 种，不选择 \(n_i\) 的方案有 \(\displaystyle\binom{n-1}{k}\) 种;

2）考虑 \(n\) 个物体中挑选 \(k\) 个，选择 \(n_i\) 的方案有 \(\displaystyle\binom{n-1}{k-1}\) 种，每一个 \(n_i\) 都被尝试选择，重复计算 \(k\) 次.

3）联立 1）2）即证.

\(52.\quad\) 证明：

\[\Gamma(x)=\lim_{n\rightarrow\infty}n^x\frac{n(n-1)\cdots1}{x(x+1)\cdots(x+n)}. \]

\[\begin{aligned} \Gamma(x)=&\int_0^{+\infty} \text e^{-t} t^{x-1} \text dt\\ =&\lim_{n\rightarrow\infty}\int_0^n (1-\frac{t}{n})^n t^{x-1} \text dt\\ =&\lim_{n\rightarrow\infty} n^x\int_0^1 (1-t)^n t^{x-1} \text dt\\ =&\lim_{n\rightarrow\infty} n^x \frac{\Gamma(n+1)\Gamma(x)}{\Gamma(n+x+1)}\\ =&\lim_{n\rightarrow\infty} n^x \frac{n!}{(x)_{n+1}} \end{aligned} \]

\(53.\quad\) 证明 Riemann 函数

\[R(x)=\begin{cases} \dfrac1q\quad x=\dfrac{p}{q},\text{gcd}(p,q)=1\\ 0\quad x\in\mathbb R- \mathbb Q \end{cases} \]

在无理点上连续，在有理点上间断.

1）设 \(x_0\) 为有理点，\(R(x_0)=\frac1q>0\)，由无理点的稠密性，存在无理点列 \(\{x_n\}\rightarrow x_0\)，但

\[|R(x_n)-R(x_0)|=|0-\frac1q|=\frac1q>0 \]

即 \(R(x_n)\) 不趋于 \(R(x_0)\)，故 \(R(x)\) 在有理点不连续；
2）设 \(x_0\in[0,1]\) 为无理点，\(R(x_0)=0\)，考虑到对于任意 \(\varepsilon>0\)，\(R(x)\geq \varepsilon\) 的点仅为有限个，如此可取 \(\delta>0\) 充分小，使 \((x_0-\delta,x_0+\delta)\) 不含有 \(R(x)\geq\varepsilon\) 的点，从而

\[\forall x\in(x_0-\delta,x_0+\delta),|R(x)-R(x_0)|=R(x)<\varepsilon \]

因此 \(R(x)\)在 \([0,1]\) 上的无理点连续，根据周期性可知在一切无理点上都连续.

\(54.\quad\) 设 \(f(x)=\dfrac{x+2}{x+1}\sin\dfrac{1}{x},a>0\) 为一正常数. 证明：\(f(x)\) 在 \((0,a)\) 非一致连续，在 \([a,+\infty)\) 一致连续.

1）

\[\begin{aligned} &|f(x')-f(x'')|\\ \leq&\left|\frac{x'+2}{x'+1}\sin\dfrac1{x'}-\frac{x''+2}{x''+1}\sin\dfrac1{x'}\right|+\left|\frac{x''+2}{x''+1}\sin\dfrac1{x'}-\frac{x''+2}{x''+1}\sin\dfrac1{x''}\right|\\ \leq&\left|\frac{x'+2}{x'+1}-\frac{x''+2}{x''+1}\right|+\frac{x''+2}{x''+1}\cdot 2\left|\cos\frac{\dfrac{1}{x'}+\dfrac{1}{x''}}{2}\right| \left|\sin\frac{\dfrac{1}{x'}-\dfrac{1}{x''}}{2}\right|\\ \leq& \frac{|x''-x'|}{(x'+1)(x''+1)}+(1+\frac{1}{x''+1})|\frac{1}{x'}-\frac{1}{x''}|\\ \leq&(\frac{1}{(a+1)^2}+\frac{a+2}{a^2(a+1)})|x'-x''|\equiv L|x'-x''| \end{aligned} \]

从而满足利普希茨条件，\(\forall \varepsilon>0,\exists \delta=\dfrac{\varepsilon}{L}\)，当 \(|x'-x''|<\dfrac{\varepsilon}{L}\) 时 \(|f(x')-f(x'')|<\varepsilon.\)
故 \(f\) 在 \([a,+\infty)\) 一致连续.
2）取点列 \(x'_n=\dfrac{1}{2n\pi+\dfrac{\pi}{2}},x''_n=\dfrac{1}{2n\pi-\dfrac{\pi}{2}}\)，\(n\) 充分大时

\[|x'_n-x''_n|\rightarrow 0,|f(x'_n)-f(x''_n)|>2 \]

故 \(f\) 在 \((0,a)\) 非一致连续.

\(55.\quad\) 求函数方程

\[f(x+y)+f(x-y)=2f(x)f(y) \]

在实轴上恒不小于 \(1\) 的连续解.

易证 \(f(0)=1\) 且 \(f(x)\) 是偶函数.
数学归纳：
取一点 \(c\)，则存在 \(\theta\) 满足 \(f(c)=\cosh\theta\)
令 \(x=y=c\)

\[f(2c)=2(f(c))^2-f(0)=2\cosh^2\theta-1=\cosh2\theta \]

若已得 \(f((n-2)c)=\cosh(n-2)\theta,f((n-1)c)=\cosh(n-1)\theta\)

\[f(nc)=2\cosh(n-1)\theta\cdot \cosh\theta-\cosh(n-2)\theta=\cosh n\theta \]

因此

\[\forall n\in\mathbb N,f(nc)=\cosh n\theta \]

继续数学归纳：
令 \(x=y=\dfrac{c}{2}\) 得

\[f(\frac{c}{2})=\cosh \frac12\theta \]

若已得 \(f(\dfrac{c}{2^{n-1}})=\cosh\dfrac{\theta}{2^{n-1}}\)

\[(f(\frac{c}{2^n}))^2=\frac{1}{2}(\cosh \frac{\theta}{2^{n-1}}+1)=(\cosh \frac{\theta}{2^n})^2 \]

因此

\[\forall n\in\mathbb N,f(\frac{c}{2^n})=\cosh \frac{\theta}{2^n} \]

综上所述

\[f(\frac{m}{2^n}c)=\cosh \frac{m}{2^n}\theta,\quad \forall m,n\in\mathbb N \]

考虑到 \(\forall x>0,\exists x_i\)（\(x_i\) 为 \(\dfrac{m}{2^n}\) 形式的数，这个形式的数是稠密的，故能逼近所有的点）使得

\[x_i\rightarrow x\quad (i\rightarrow\infty) \]

则 \(f(x_i c)=\cosh x_i\theta\)
由连续性可取 \(i\rightarrow\infty\) 极限

\[f(cx)=\cosh \theta x \]

亦即

\[f(x)=\cosh ax\quad (\forall x\in\mathbb R). \]

\(56.\quad\) 设 \(f_1,f_2\) 在 \(x_0\) 及其附近有定义，在 \(x_0\) 有直到 \(n\) 阶导数，记 \(N(f)=\displaystyle{\sum_{k=0}^n \frac{1}{k!}|f^{(k)}(x_0)|}\)，证明：

\[N(f_1f_2)\leq N(f_1)N(f_2). \]

\[\begin{aligned} N(f_1f_2)=&\sum_{k=0}^n \frac{1}{k!}|(f_1f_2)^{(k)}(x_0)|\\ \leq&\sum_{k=0}^n \frac{1}{k!}\sum_{j=0}^k \binom{k}{j} |f_1^{(j)}(x_0)||f_2^{(k-j)}(x_0)|\\ =&\sum_{k=0}^n\sum_{j=0}^k \frac{1}{j!(k-j)!}|f_1^{(j)}(x_0)||f_2^{(k-j)}(x_0)|\\ \leq&\sum_{j=0}^n \frac{1}{j!}|f_1^{(j)}(x_0)|\cdot\sum_{k=0}^n \frac1{k!}|f_2^{(k)}(x_0)|\\ =&N(f_1)\cdot N(f_2) \end{aligned} \]

\(57.\quad\) 设 \((a,b)\) 为有穷或无穷区间，\(f(x)\) 在 \((a,b)\) 内可微，且 \(\displaystyle{\lim_{x\rightarrow a^+}f(x)=\lim_{x\rightarrow b^-}f(x)=A}\) (有限或 \(\pm\infty\))，证明：\(\exists \xi\in (a,b)\)，使得 \(f'(\xi)=0.\)

1）若为常函数，则问题自明.
2）若 \(f(x)\) 不恒等于 \(A\)，则存在 \(x_0\in(a,b)\)，使得 \(f(x_0)\neq A\)，不妨设 \(f(x_0)>A\)，考虑到连续性可取任意 \(\mu\ (A<\mu<f(x_0))\)，那么存在 \(x_1\in(a,x_0),x_2\in(x_0,b)\) 使得 \(f(x_1)=f(x_2)=\mu\)，从而存在 \(\xi\in(x_1,x_2)\subset(a,b),f'(\xi)=0.\)

\(58.\quad\) 证明：Legendre 多项式

\[P_n(x)=\frac{1}{2^n n!}\frac{\text d^n}{\text dx^n}|(x^2-1)^n| \]

的一切根在 \((-1,1)\) 内.

我们将本题推广一下：
设 \(P_n(x)=a_0x^n+a_1x^{n-1}+\cdots+a_n\) 为实系数多项式，且一切根皆为实数，那么导数 \(P'_n(x),\cdots,P^{(n-1)}_n(x)\) 也仅有实根.

可设 \(P_n(x)=a_0(x-\alpha_1)^{k_1}\cdots(x-\alpha_m)^{k_m}\)，由 Rolle 定理 \('_n(x)\) 在相异的 \(m\) 个根间隙里有 \(m-1\) 个根.
对于 \(P_n(x)\) 的 \(k_i\) 重根，它必为 \(P'_n(x)\) 的 \(k_{i}-1\) 重根.
因此 \(P'_n(x)\) 共有 \((m-1)+(k_1-1)+\cdots+(k_m-1)=n-1\) 个根.

\(59.\quad\) 设 \(f(x)\) 在 \([a,b]\) 上有 \(n\) 阶连续导数，且 \(f(x)\) 在 \([a,b]\) 上至少有 \(n+1\) 个不同实根. 证明：

\[P_n(D)f(x)\equiv (D^n+c_{n-1}D^{n-1}+\cdots+c_0)f(x) \]

在 \([a,b]\) 至少有一零点.（\(P_n(x)\) 为仅有实根的实系数多项式）

注意到

\[P_n(D)f(x)=(D-\alpha_1)\cdots(D-\alpha_n)f(x) \]

其中在 \(f(x)\) 的不同实根之间必有

\[(D-\alpha_n)f(x)=f'(x)-\alpha_n f(x) \]

的一个实根（考虑构造 \(g(x)=f(x)\text e^{-\alpha x}\) 利用 Rolle 定理），共 \(n\) 个. 如此这般重复 \(n-1\) 次，\((D^n+c_{n-1}D^{n-1}+\cdots+c_0)f(x)\) 至少有一实根.

\(60.\quad\) 设 \(f,g,h\) 在 \([a,b]\) 连续，在 \((a,b)\) 可导，证明：

\[\left|\begin{matrix} f(a)&g(a)&h(a)\\ f(b)&g(b)&h(b)\\ f'(\xi)&g'(\xi)&h'(\xi) \end{matrix}\right|=0 \]

这题是 Lagrange 和 Cauchy 中值定理的推广，记：

\[F(x)=\left|\begin{matrix} f(a)&g(a)&h(a)\\ f(b)&g(b)&h(b)\\ f(x)&g(x)&h(x) \end{matrix}\right| \]

由 Rolle 定理 \(F(a)=F(b)=0,F'(\xi)=0\)
证毕.

\(61.\quad\) 设 \(f(x)\) 在包含 \(x_0\) 的区间 \(I\) 上二次可微，\(x_0+h\in I,\lambda\in(0,1)\)，证明：\(\exists \theta\in(0,1)\) 使得

\[f(x_0+\lambda h)=\lambda f(x_0+h)+(1-\lambda)f(x_0)+\frac{\lambda}{2}(\lambda-1)h^2f''(x_0+\theta h). \]

利用K值法（含 \(\theta\) 项设为 \(K\)）
令 \(F(t)=f(x_0+th)-tf(x_0+h)-(1-t)f(x_0)-\dfrac{t}{2}(t-1)h^2K\)
考虑到 \(F(0)=F(1)=F(\lambda)=0\)
两次应用 Rolle 定理得

\[F''(\theta)=0 \]

此式即

\[K=f''(x_0+\theta h) \]

\(62.\quad\) 若函数 \(f(x)\) 在 \((a,b)\) 可微，且 \(\displaystyle{\lim_{x\rightarrow a^+}f(x)=\infty}\)，证明

\[\overline{\lim_{x\rightarrow a^+}}f'(x)=\infty \]

这里 \(\overline{\lim}\) 指的是上极限（可理解为最大的子列极限，或者说是子列极限的上确界），要证 \(\displaystyle{\overline{\lim_{x\rightarrow a^+}}f'(x)=\infty}\)，只要证明存在序列 \(\{\xi_n\}\rightarrow a+0\) 使得 \(\displaystyle{\lim_{n\rightarrow\infty}|f'(\xi_n)|=+\infty}\).

记 \(l=b-a,c_n=a+\dfrac{l}{n}=a+\dfrac{b-a}{n}\)，则 \(n\rightarrow\infty\) 时 \(c_n\rightarrow a+0\).
由于 \(\displaystyle{\lim_{x\rightarrow a^+}f(x)=\infty}\)，可取 \(x_1\in(a,c_1)\) 使得 \(|f(x_1)-f(c_1)|>l\)，从而应用 Lagrange 定理

\[|f'(\xi_n)|=\left|\frac{f(x_1)-f(c_1)}{x_1-c_1}\right|>\frac{|f(x_1)-f(c_1)|}{l}>1 \]

同理存在 \(x_n\in(a,c_n)\) 使得 \(|f(x_n)-f(c_n)|>nl\) 从而 \(|f'(\xi_n)|>n\)
如此我们得到

\[\xi_n\rightarrow a,|f'(\xi_n)|\rightarrow +\infty \]

总结一些插值方法：Lagrange, Newton, Hermite.

Lagrange 的基本原理是计算基函数 \(\displaystyle{l_i(x)=\prod_{j=0\\j\neq i}^n \frac{x-x_j}{x_i-x_j}}\) 的线性组合，Newton 的基本原理是用过均差 \(f(a,b,c,\cdots)\) 递推，Hermite 是高阶导数版的 Newton. 注意一些常识：插值多项式是唯一的；插值次数比节点数小 \(1\)；通常记为 \(f(x)=f_2(x)+R_2(x)\) 的形式中，下标 \(2\) 代表次数，实际上是插值了 \(3\) 个点，\(R_2(x)\) 也常常用一个三阶导数来代替.

Darboux 定理：\(f'(a)<\eta<f'(b)\Rightarrow f'(c)=\eta,c\in(a,b)\)

\(63.\quad\) 设 \(f(x)\) 在区间 \([0,1]\) 可微，\(f(0)=0,f(1)=1,k_i>0\). 证明存在互不相等的 \(x_i\) 满足

\[\sum_{i=1}^n \frac{k_i}{f'(x_i)}=\sum_{i=1}^n k_i \]

本题实质上是证明

\[\sum_{i=1}^n \frac{\lambda_i}{f'(x_i)}=1,0<\lambda_i<1,\lambda_1+\cdots+\lambda_n=1 \]

由介值定理存在 \(0<c_1<c_2<\cdots<c_n=1\) 使得

\[\begin{aligned} &f(c_1)=\lambda_1\\ &f(c_2)=\lambda_1+\lambda_2\\ &\cdots\\ &f(c_n)=\lambda_1+\cdots+\lambda_n \end{aligned} \]

由 Lagrange 定理

\[f'(x_i)=\frac{f(c_i)-f(c_{i-1})}{c_i-c_{i-1}}=\frac{\lambda_i}{c_i-c_{i-1}} \]

\[\frac{\lambda_i}{f'(x_i)}=c_i-c_{i-1} \]

累加即有

\[\sum_{i=1}^n \frac{\lambda_i}{f'(x_i)}=1,0<\lambda_i<1,\lambda_1+\cdots+\lambda_n=1 \]

令 \(\lambda_i=\dfrac{k_i}{\displaystyle{\sum_{i=1}^n k_i}}\)

\[\sum_{i=1}^n \frac{k_i}{f'(x_i)}=\sum_{i=1}^n k_i \]

\(64.\quad\) \(f(x)\) 在 \([0,1]\) 可导，\(2f'(\dfrac{1}{3})\neq f'(\dfrac{2}{3})\)，证明存在互不相同的 \(\theta_1,\theta_2,\theta_3\in(0,1)\) 满足

\[\frac{f'(\theta_1)}{\theta_1}+\frac{f'(\theta_2)}{\theta_2}=2\frac{f'(\theta_3)}{\theta_3} \]

令 \(\theta_1=\dfrac13,\theta_2=\dfrac23\)，不妨设 \(\dfrac{f'(\theta_1)}{\theta_1}<\dfrac{f'(\theta_2)}{\theta_2}\)，令 \(c=\dfrac12\left(\dfrac{f'(\theta_1)}{\theta_1}+\dfrac{f'(\theta_2)}{\theta_2}\right)\)，\(g(x)=f(x)-\dfrac{c}{2}x^2\)，则 \(g'(\theta_1)<0,g'(\theta_2)>0\)，由 Darboux 定理 \(g'(\theta_3)=0\) 即 \(\dfrac{f'(\theta_3)}{\theta_3}=c\)

\(65.\quad\) 证明 Jenson 不等式：设 \(f(x)\) 在 \([a,b]\) 上二次可微，\(f''(x)<0\)，\(\forall a\leq x_1<x_2<\cdots<x_n\leq b,k_i\geq0\)，\(\displaystyle{\sum_{i=1}^n k_i=1}\)

\[f\left(\sum_{i=1}^n k_ix_i\right)>\sum_{i=1}^n k_if(x_i). \]

取 \(x_0=\displaystyle\sum_{i=1}^n k_ix_i\)，将 \(f(x)\) 在 \(x=x_0\) 展开

\[\begin{aligned} f(x_i)=&f(x_0)+f'(x_0)(x_i-x_0)+\dfrac12 f''(\xi)(x_i-x_0)^2\\ <& f(x_0)+f'(x_0)(x_i-x_0) \end{aligned} \]

用 \(k_i\) 乘以两端并相加

\[\displaystyle\sum_{i=1}^n k_i(x_i-x_0)=\sum_{i=1}^n k_ix_i-x_0=0 \]

因此

\[\sum_{i=1}^n k_if(x_i)<f(x_0)=f\left(\sum_{i=1}^n k_ix_i\right). \]

\(66.\quad\) 设 \(f(x)\) 在 \([0,1]\) 上有二阶导数，\(0\leq x\leq1\) 时 \(|f(x)|\leq 1,|f''(x)|<2\). 证明：当 \(0\leq x\leq 1\) 时

\[|f'(x)|\leq 3. \]

如果采用这样的做法：
对 0,1 采用 Newton 插值：

\[f(x)=f(0)+f(0,1)x+\dfrac{f''(\xi)}{2}x(x-1) \]

因此

\[\begin{aligned} |f'(x)|=&\left|f(0,1)+(2x-1)\cdot\frac{f''(\xi)}{2}\right|\\ \leq& |f(1)-f(0)|+|x-\frac12||f''(\xi)|\\ \leq& 2+\frac12\cdot 2\\ =&3 \end{aligned} \]

其实是不对的，因为 \(\xi\) 是 \(x\) 的函数，不可以对等式两端关于 \(x\) 求导.

正确的做法是直接

\[f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(\xi)}{2}(x-x_0)^2 \]

从而

\[f'(x_0)=\frac{f(x)-f(x_0)}{x-x_0}-\frac12 f''(\xi)(x-x_0) \]

位于 \([-3,3]\) 中.

\(67.\quad\)

\[ \int_0^\infty \frac{\sin{ax}}{\text e^x-1} dx \] (Rectangular contour) Let \[f(z)=\dfrac{\text e^{\text iaz}}{\text e^z-1}\] \[ (1-\text e^{-2a\pi})I-\text i\frac{\pi}{2}\text e^{-2a\pi}-\text i\frac{\pi}{2}-\int_\gamma f(z)dz=0 \]

\[\] $\gamma$ represents the line from $(0,0)$ to $(0,2\pi)$. For \[ \int_0^{2\pi} \frac{\text e^{\text iaz}}{\text e^z-1}dz \] We need to evaluate the imaginary part: \[ \begin{aligned} \text i\int_0^{2\pi} \frac{\text e^{-ay}}{\text e^{\text iy}-1}dy= & \text i\int_0^{2\pi}\frac{\text e^{-ay}}{\cos y+\text i\sin y-1}dy \\ = & \text i\int_0^{2\pi}\frac{\text e^{-ay}(-1-\text i\cot\frac{y}{2})}{2}dy \\ = & \text i\int_0^{2\pi}-\frac12\text e^{-ay}dy \\ = & \text i\frac{\text e^{-2\pi a}-1}{2a} \end{aligned} \] Hence \[ I=\frac{\pi}{2}\coth(\pi a)-\frac{1}{2a} \]

\(68.\quad\)

\[\int_{-1}^1 \dfrac{\sqrt[4]{(1-x)^3(1+x)}}{x^2+1}\text dx \]

Let \(h(z)=\sqrt[4]{(1-z)^3(1+z)}\), we have to figure out the right branch and arguments while evaluating \(h(\text i)\).
For that we choose the \(k=0\) branch and set the arguments above the real axis \(\text{arg}(1+z)=\text{arg}(1-z)=0\), indicating

\[h(z)=\sqrt[4]{|1-z|^3|1+z|}\text e^{\text i\frac{3\Delta\text{arg}(1-z)+\Delta\text{arg}(1+z)}{4}} \]

Draw a curve (arbitrarily) that doesn't cut across \([-1,1]\), for branch point \((-1,0)\) it turned \(\dfrac{\pi}{4}\), and for \((1,0)\) it turned \(-\dfrac{\pi}{4}\).

Therefore

\[h(\text i)=\sqrt[4]{|1-\text i|^3|1+\text i|}\text e^{\text i\frac{3(-\frac\pi4)+\frac\pi4}{4}}=\sqrt 2 \text e^{-\frac\pi8\text i} \]

Similarly, as we evaluate \(\displaystyle{\lim_{z\rightarrow \infty}z(z-a)^r(b-z)^sf(z)}\)

It could be interpreted as

\[\begin{aligned} \lim_{z\rightarrow \infty}z(z-a)^r(b-z)^sf(z)=&\lim_{z\rightarrow \infty}z|z|^r\text e^{r\theta\text i}|z|^s\text e^{s(\theta-\pi)\text i}f(z)\\ =&\text e^{-s\pi\text i}\lim_{z\rightarrow \infty}z^{r+s+1}f(z)\\ =&\text e^{-s\pi\text i}A \end{aligned} \]

Now turn back to the original question:
Let

\[f(z)=\dfrac{\sqrt[4]{(1-z)^3(1+z)}}{z^2+1} \]

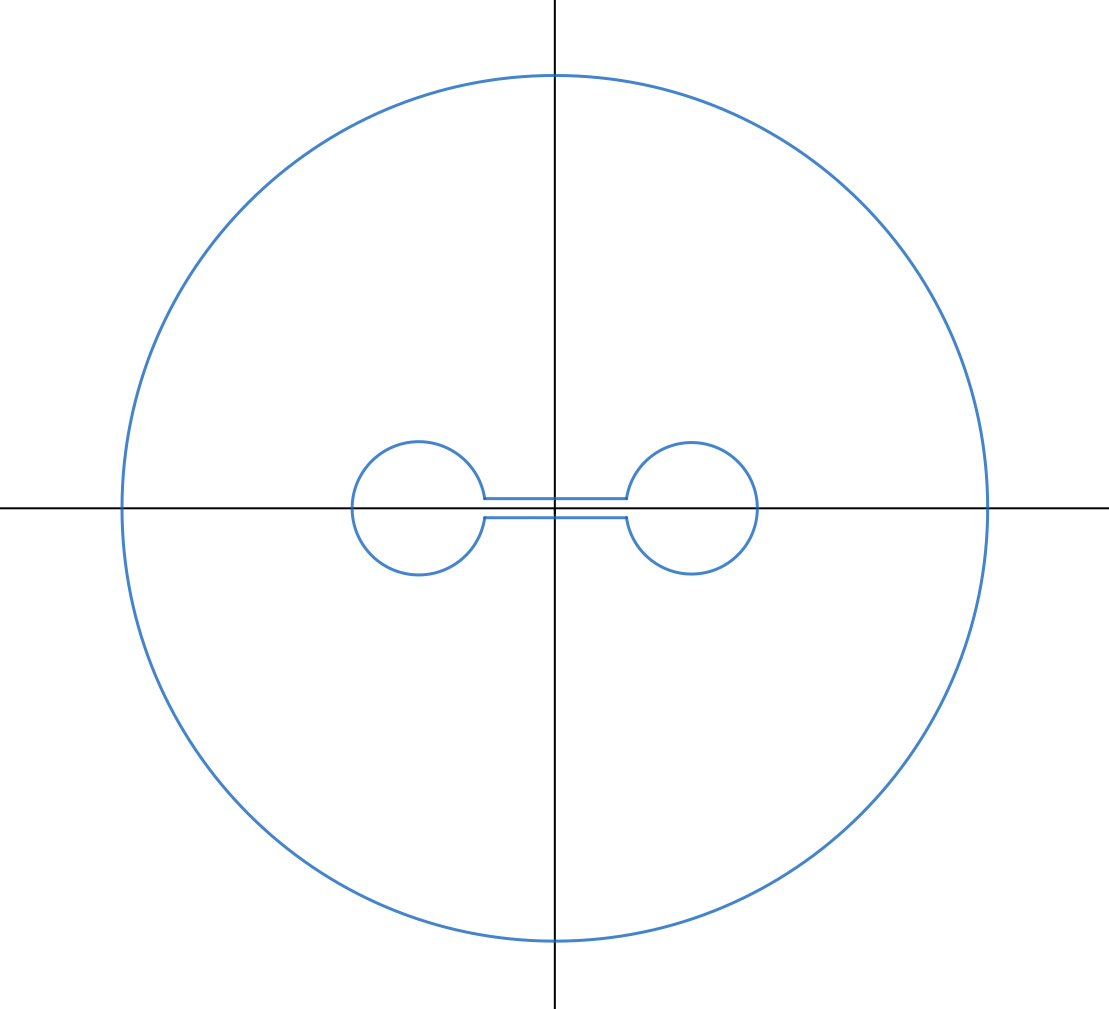
The upper segment represents \(\dfrac{\sqrt[4]{(1-x)^3(1+x)}}{x^2+1}\)
The lower segment represents \(\dfrac{\sqrt[4]{(1-x)^3(1+x)}}{x^2+1}\text e^{\frac{3\pi}2\text i}=-\text i\dfrac{\sqrt[4]{(1-x)^3(1+x)}}{x^2+1}\)
And by the residue formula:

\[\begin{aligned} 2\pi\text i\text e^{-\frac{3\pi}{4}\text i}-(1+\text i)I&=2\pi\text i(\text{Res}[f(z),\text i]+\text{Res}[f(z),-\text i])\\ I&=-\frac{\pi}{\sqrt2}\left(2-\sqrt2(\text e^{-\frac{\pi}8\text i}+\text e^{\frac\pi8\text i})\right)\\ I&=\pi\left(\sqrt{2+\sqrt{2}}-\sqrt2\right) \end{aligned} \]

\(69.\quad\)

\[\lim_{n\rightarrow\infty}\frac{[1^\alpha+3^\alpha+\cdots+(2n+1)^\alpha]^{\beta+1}}{[2^\beta+4^\beta+\cdots+(2n)^\beta]^{\alpha+1}]} \]

\[\begin{aligned} \frac{[1^\alpha+3^\alpha+\cdots+(2n+1)^\alpha]^{\beta+1}}{[2^\beta+4^\beta+\cdots+(2n)^\beta]^{\alpha+1}]} =& 2^{\alpha-\beta}\frac{\{\dfrac{2}{n}[(\dfrac1n^\alpha+\cdots+(\dfrac{2n+1}{n})^\alpha]\}^{\beta+1}}{\{\dfrac{2}{n}[(\dfrac2n^\beta+\cdots+(\dfrac{2n}{n})^\beta]\}^{\alpha+1}}\\ =&2^{\alpha-\beta}\frac{[\displaystyle\sum_{i=1}^n(\dfrac{2i-1}{n})^\alpha \dfrac2n]^{\beta+1}}{[\displaystyle\sum_{i=1}^n(\dfrac{2i}{n})^\beta \dfrac2n]^{\alpha+1}}\\ \rightarrow&2^{\alpha-\beta}\frac{(\displaystyle\int_0^2 t^\alpha \text dt)^{\beta+1}}{(\displaystyle\int_0^2 t^\beta \text dt)^{\alpha+1}}\\ =&2^{\alpha-\beta}\frac{(\beta+1)^{\alpha+1}}{(\alpha+1)^{\beta+1}} \end{aligned} \]

\(70.\quad\)

\[\lim_{n\rightarrow\infty}\sum_{i=0}^{n-1}b^{\frac{i}{n}}\sin b^{\frac{2i+1}{2n}} \]

\[\sum_{i=0}^{n-1}b^{\frac{i}{n}}\sin b^{\frac{2i+1}{2n}}=\sum_{i=0}^{n-1}(\sin b^{\frac{2i+1}{2n}})(b^{\frac{i+1}{n}}-b^{\frac{i}{n}}) \]

这可理解为 \(\sin x\) 在区间 \([1,b]\) 上的 \(n\) 分划

\[\sum_{i=0}^{n-1}(\sin b^{\frac{2i+1}{2n}})(b^{\frac{i+1}{n}}-b^{\frac{i}{n}})\rightarrow\int_1^b \sin x\text dx=\cos1-\cos b. \]

\(71.\quad\) 证明 Wallis 公式：

\[\left(\frac{(2n)!!}{(2n-1)!!}\right)^2\frac{1}{2n+1}\rightarrow\frac{\pi}{2} \]

考虑积分 \(I_n=\displaystyle\int_0^\frac\pi2 \sin^n x\text dx\)
由分部积分可得

\[I_n=\frac{n-1}{n}I_{n-2} \]

那么

\[I_{2k+1}<I_{2k}<I_{2k-1} \]

\[\frac{(2k)!!}{(2k+1)!!}<\frac{(2k-1)!!}{(2k)!!}\frac{\pi}{2}<\frac{(2k-2)!!}{(2k-1)!!} \]

变形

\[1<\frac{(2k-1)!!(2k+1)!!}{[(2k)!!]^2}\frac\pi2<\frac{2k+1}{2k} \]

由夹逼定理得证.
从中我们还可以得知

\[\frac{(2n)!!}{(2n-1)!!}\sim\sqrt{n\pi} \]

\(72.\quad\) 证明 Abel-Dirichlet 判别法：
满足下列两个条件之一，则 \(\displaystyle\int_a^{+\infty}f(x)g(x)\text dx\) 收敛
1）\(\displaystyle\int_a^{+\infty}f(x)\text dx\) 收敛，\(g(x)\) 单调有界（Abel）
2）\(\displaystyle\int_a^A f(x)\text dx\) 有界，\(g(x)\) 单调且 \(\displaystyle\lim_{x\rightarrow+\infty}g(x)=0\)（Dirichlet）

证明前先说明积分第一，第二中值定理：
1）如果 \(g(x)\) 不变号，那么

\[\int_a^b f(x)g(x)\text dx=f(\xi)\int_a^b g(x)\text dx \]

为什么 \(g(x)\) 不能变号呢？可能出现 \(f(x)\) 恒大于 \(0\)，\(\displaystyle\int_a^b g(x)\text dx<0\)，\(\displaystyle\int_a^b f(x)g(x)\text dx>0\) 的情况.
2）如果 \(g(x)\) 单调，那么

\[\int_a^b f(x)g(x)\text dx=g(a)\int_a^\xi f(x)\text dx+g(b)\int_\xi^b f(x)\text dx \]

为什么 \(g(x)\) 要单调呢？可能出现 \(f(x)\) 恒大于 \(0\)，\(\xi\) 取端点值 \(g(a)\displaystyle\int_a^b f(x)\text dx\) 和 \(g(b)\displaystyle\int_a^b f(x)\text dx\) 都比 \(\displaystyle\int_a^b f(x)g(x)\text dx\) 大的情况.
以上都可借助 \(f-g-x\) 坐标系加以理解.

先证 Abel 判别法：

\[\begin{aligned} |\int_A^B f(x)g(x)\text dx|=&|g(A)\int_A^\xi f(x)\text dx|+|g(B)\int_\xi^B f(x)\text dx|\\ \leq&2 g_{\text{max}}\cdot \varepsilon_1\\ =&\varepsilon \end{aligned} \]

再证 Dirichlet 判别法：

\[\begin{aligned} |\int_A^B f(x)g(x)\text dx|=&|g(A)\int_A^\xi f(x)\text dx|+|g(B)\int_\xi^B f(x)\text dx|\\ \leq& 2M\cdot\varepsilon_1\\ =&\varepsilon \end{aligned} \]

\(73.\quad\)

\[\lim_{h\rightarrow0}\int_0^1 \frac{h}{h^2+x^2}f(x)\text dx=\frac{\pi}{2}f(0). \]

很容易证明 \(\varepsilon\rightarrow 0\) 时

\[\int_0^\varepsilon \frac{h}{h^2+x^2}f(x)\text dx\rightarrow\frac{\pi}{2}f(0) \]

因此考虑取一个趋近 \(0\) 的分点 \(\varepsilon\)，下证

\[\int_\varepsilon^1 \frac{h}{h^2+x^2}f(x)\text dx\rightarrow0 \]

\[\begin{aligned} |\int_\varepsilon^1 \frac{h}{h^2+x^2}f(x)\text dx|\leq& M\int_\varepsilon^1 \frac{h}{h^2+x^2}\text dx\\ =& M(\arctan\frac{1}{h}-\arctan\frac{\varepsilon}{h})\\ \rightarrow& 0 \end{aligned} \]

\(74.\quad\) 证明

\[\int_0^1 |f(x)|\text dx\leq \text{max}\left\{\int_0^1 |f'(x)|\text dx,\left|\int_0^1 f(x)\text dx\right|\right\} \]

只证 \(\displaystyle{\left|\int_0^1 f(x)\text dx\right|<\int_0^1 |f(x)|\text dx}\) 的情况 (存在零点 \(x_0\)):

\[\begin{aligned} |f(x)|=&|f(x)-f(x_0)|\\ =&\left|\int_{x_0}^x f'(x)\text dx\right|\\ \leq& \int_{x_0}^x |f'(x)|\text dx\\ \leq&\int_0^1 |f'(x)|\text dx \end{aligned} \]

那么

\[\int_0^1 |f(x)|\text dx=|f(\xi)|\int_0^1\text dx\leq\int_0^1 |f'(x)|\text dx \]

\(75.\quad\) 设 \((f(x_1)-f(x_2))(g(x_1)-g(x_2))\geq0\), 证明:

\[\int_a^b f(x)\text dx\int_a^b g(x)\text dx\leq(b-a)\int_a^b f(x)g(x)\text dx \]

先对 \(x_1\) 积分，后对 \(x_2\) 积分

\[\begin{aligned} \int_a^b \int_a^b (f(x_1)-f(x_2))(g(x_1)-g(x_2))\text dx_1\text dx_2&\geq 0 \end{aligned} \]

化简得

\[\int_a^b f(x)\text dx\int_a^b g(x)\text dx\leq(b-a)\int_a^b f(x)g(x)\text dx \]

这被称作似序不等式. 不等号反向则称作反序不等式.

\(76.\quad\) 设 \(f'(x)\) 在 \([a,b]\) 连续，证明

\[\mathop{\text{max}}\limits_{a\leq x\leq b}|f(x)|\leq \left|\frac{1}{b-a}\int_a^b f(x)\text dx\right|+\int_a^b |f'(x)|\text dx \]

考虑积分中值定理

\[|f(\xi)|=\left|\frac1{b-a}\int_a^b f(x)\text dx\right| \]

利用

\[\mathop{\text{max}}\limits_{a\leq x\leq b}|f(x)|=|f(x_0)|=\left|\int_\xi^{x_0}f'(t)\text dt+f(\xi)\right| \]

完成证明.

\(77.\quad\) 设 \(f(x)\) 二次可微，证明在 \((a,b)\) 内存在一点 \(\xi\)

\[f''(\xi)=\frac{24}{(b-a)^3}\int_a^b \left(f(x)-f(\frac{a+b}{2})\right)\text dx \]

设 \(F(x)\) 是原函数，采用 Hermite 插值

\[6F(a,\frac{a+b}{2},\frac{a+b}{2},b)=F'''(\xi) \]

化简得

\[f''(\xi)=\frac{24}{(b-a)^3}\int_a^b \left(f(x)-f(\frac{a+b}{2})\right)\text dx \]

经验: 可微 \(\Leftrightarrow\) 可导 \(\Rightarrow\) 连续 \(\Rightarrow\) 存在原函数 \(\Rightarrow\) 可积

\(78.\quad\) (Hadamard 定理) 设 \(f(x)\) 是 \([a,b]\) 上连续的凸函数. 证明

\[f(\frac{x_1+x_2}{2})\leq\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(t)\text dt\leq \frac{f(x_1)+f(x_2)}{2} \]

仿照琴生的证明，设 \(t=x_1+\lambda(x_2-x_1)\)

\[\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(t)\text dt=\int_0^1 f[x_1+\lambda(x_2-x_1)]\text d\lambda \]

同理

\[\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(t)\text dt=\int_0^1 f[x_2-\lambda(x_2-x_1)]\text d\lambda \]

因此

\[\begin{aligned} &\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(t)\text dt\\ =&\frac{1}{2}\int_0^1(f[x_1+\lambda(x_2-x_1)]+f[x_2-\lambda(x_2-x_1)])\text d\lambda\\ \geq& f(\frac{x_1+x_2}{2}) \end{aligned} \]

另一方面

\[\begin{aligned} &\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(t)\text dt\\ =&\int_0^1 f[\lambda x_2+(1-\lambda)x_1]\text d\lambda\\ \leq& \int_0^1 [\lambda f(x_2)+(1-\lambda)f(x_1)]\text d\lambda\\ =&\frac{f(x_1)+f(x_2)}{2} \end{aligned} \]

\(79.\quad\) 设 \(f(x),p(x)\) 在 \([a,b]\) 连续，\(p(x)\geq0,\int_a^b p(x)\text dx>0\)，且 \(m\leq f(x)\leq M\)，\(\varphi(x)\) 在 \([m,M]\) 上有定义，并有二阶导数，\(\varphi''(x)>0\)，证明

\[\varphi\left(\frac{\int_a^b p(x)f(x)\text dx}{\int_a^b p(x)\text dx}\right)\leq\frac{\int_a^b p(x)\varphi(f(x))\text dx}{\int_a^b p(x)\text dx} \]

由凸函数知

\[\varphi\left(\frac{p_1f_1+\cdots+p_nf_n}{p_1+\cdots+p_n}\right)\leq \frac{p_1\varphi(f_1)+\cdots+p_n\varphi(f_n)}{p_1+\cdots+p_n} \]

设 \(x_i=a+\dfrac{i}{n}(b-a)\)

\[\varphi\left(\frac{\sum p(x_i)f(x_i)\dfrac{b-a}{n}}{\sum p(x_i)\dfrac{b-a}{n}}\right)\leq\frac{\sum p(x_i)\varphi(f(x_i))\dfrac{b-a}{n}}{\sum p(x_i)\dfrac{b-a}{n}} \]

令 \(n\rightarrow\infty\) 得欲证式.

\(80.\quad\) 对区间 \([a,b]\)，若 \(g'\) 连续，\(g(a)=0\)，证明

\[\int_a^b |g(x)g'(x)|\text dx\leq \frac{b-a}{2}\int_a^b (g'(x))^2 \text dx \]

想办法往 Cauchy 不等式上凑：
设 \(f(x)=\displaystyle\int_a^x |g'(t)|\text dt\)，那么

\[\begin{aligned} f'(x)=&|g'(x)|\\ |g(x)|=&|g(x)-g(a)|\\ =&|\int_a^x g'(t)\text dt|\\ \leq&\int_a^x |g'(t)|\text dt\\ =&f(x) \end{aligned} \]

这样

\[\begin{aligned} \int_a^b |g(x)g'(x)|\text dx\leq&\int_a^b f(x)f'(x)\text dx\\ =&\int_a^b f(x)\text df(x)\\ =&\frac12 f^2(x)\bigg|_a^b\\ =&\frac12(\int_a^b |g'(t)|\text dt)^2\\ \leq& \frac{b-a}{2}\int_a^b (g'(x))^2 \text dx \end{aligned} \]

\(81.\quad\) 证明变限积分求导公式：

\[\frac{\partial}{\partial x}\left(\int_{l(x)}^{u(x)}f(x,t)\text dt\right)=\int_{l(x)}^{u(x)}f^{(1,0)}(x,t)\text dt+u'(x)f(x,u(x))-l'(x)f(x,l(x)) \]

设 \(F(x,t)=\displaystyle\int_0^t f(x,t)\text dt\)，即 \(f(x,t)=F^{(0,1)}(x,t)\)，那么

\[\begin{aligned} \frac{\partial}{\partial x}\left(\int_{l(x)}^{u(x)}f(x,t)\text dt\right)=& \frac{\partial}{\partial x}\left(F(x,u(x))-F(x,l(x))\right)\\ =&F^{(1,0)}(x,u(x))+F^{(0,1)}(x,u(x))u'(x)\\&-F^{(1,0)}(x,l(x))-F^{(0,1)}(x,l(x))l'(x)\\ =&\int_{l(x)}^{u(x)}f^{(1,0)}(x,t)\text dt+u'(x)f(x,u(x))-l'(x)f(x,l(x)) \end{aligned} \]

\(82.\quad\) \(f(x)\) 在闭区间 \([a,b]\) 上有连续 \(n\) 阶导数 \(f^{(n)}(x)\), 并且 \(f^{(k)}(a)=0\), \(k=0,1,\cdots,n-1\), 求证

\[\left(\int_a^b (f^{(k)}(x))^2 \text dx \right)^{\frac12}\leq \left(\frac12\right)^{\frac{m-k}{2}}(b-a)^{m-k}\left[\int_a^b(f^{(m)}(x))^2\text dx\right]^{\frac12} \]

如果设 \(\varphi(x)=f^{(k)}(x), m-k=d\), 那么本题实际上是

\[\left(\int_a^b[\varphi(x)]^2\text dx\right)^\frac12\leq \left(\frac12\right)^{\frac{d}{2}}(b-a)^d \left[\int_a^b[\varphi^{(d)}(x)]^2\text dx\right]^{\frac12} \]

显然只需证明递推关系

\[\left(\int_a^b[\varphi(x)]^2\text dx\right)^\frac12\leq \left(\frac12\right)^{\frac{1}{2}}(b-a) \left[\int_a^b[\varphi'(x)]^2\text dx\right]^{\frac12} \]

为把 \(\varphi\) 和 \(\varphi'\) 联系起来

\[\varphi(x)=\int_a^x \varphi'(x)\text dx \]

因此

\[\begin{aligned} (\varphi(x))^2=&\left(\int_a^x \varphi'(t)\text dt\right)^2\leq\int_a^x 1^2\text dt\cdot\int_a^x (\varphi'(t))^2\text dt\\ =&(x-a)\int_a^x\varphi'^2(t)\text dt \end{aligned} \]

两边同时积分

\[\begin{aligned} \int_a^b (\varphi(x))^2\text dx\leq&\int_a^b \left((x-a)\int_a^x\varphi'^2(t)\text dt\right)\text dx\\ =&\frac12\int_a^b \left(\int_a^x\varphi'^2(t)\text dt\right)\text d(x-a)^2\\ =&\frac12(x-a)^2\left(\int_a^x\varphi'^2(t)\text dt\right)\bigg|_{x=a}^{x=b}\\ &-\frac12\int_a^b(x-a)^2\varphi'^2(x)\text dx\\ \leq&\frac12(b-a)^2\int_a^b \varphi'^2(t)\text dt \end{aligned} \]

此题告诉了我们一个函数与其任意阶导数的不等式.

\(83.\quad\) 证明 \(\displaystyle{\lim_{n\rightarrow\infty}\sqrt[n]{x_n}=\lim_{n\rightarrow\infty}\frac{x_{n+1}}{x_n}}\), 其中 \(x_n>0\)

本质上是数列极限等于算数均值极限等于几何均值极限.

\[\begin{aligned} \lim_{n\rightarrow\infty}\sqrt[n]{x_n}=&\lim_{n\rightarrow\infty}\sqrt[n]{x_1}\sqrt[n]{\left(\frac{x_2}{x_1}\right)\cdots\left(\frac{x_n}{x_{n-1}}\right)}=\lim_{n\rightarrow\infty}\frac{x_n}{x_{n-1}} \end{aligned} \]

注意这个结论只能在数列恒正的时候用.

\(84.\quad\) 设 \(f(x)\geq0,g(x)>0\), 二函数在 \([a,b]\) 连续, 证明

\[\lim_{n\rightarrow\infty}\left(\int_a^b(f(x))^ng(x)\text dx\right)^{\frac1n}=\mathop{\text{max}}\limits_{a\leq x\leq b}f(x) \]

显然用夹逼定理.
记 \(\mathop{\text{max}}\limits_{a\leq x\leq b}f(x)=M\)
则

\[\left(\int_a^b(f(x))^ng(x)\text dx\right)^{\frac1n}\leq M\left(\int_a^b g(x)\text dx\right)^{\frac1n}\rightarrow M \]

另一方面 \(\forall \varepsilon>0, \exists [\alpha,\beta]\subset[a,b]\),

\[f(x)>M-\varepsilon \]

因此

\[\left(\int_a^b(f(x))^ng(x)\text dx\right)^{\frac1n}\geq \left(\int_{\alpha}^{\beta}(f(x))^ng(x)\text dx\right)^{\frac1n}\geq M-\varepsilon \]

由 \(\varepsilon\) 的任意性即证.

\(85.\quad\) 设 \(f(x),g(x)\) 在 \([a,b]\) 连续, \(f(x)\) 恒不为 \(0\), \(g(x)\) 有正下界. 记 \(\displaystyle{d_n=\int_a^b|f(x)|^ng(x)\text dx}\), 证明

\[\lim_{n\rightarrow\infty}\frac{d_{n+1}}{d_n}=\mathop{\text{max}}\limits_{a\leq x\leq b}|f(x)| \]

观察形式不难发现这题需要用到单调有界.

\[\begin{aligned} d_n=&\int_a^b |f(x)|^n g(x)\text dx\\ =&\int_a^b \sqrt{g(x)}|f(x)|^{\frac{n-1}{2}}\cdot\sqrt{g(x)}|f(x)|^{\frac{n+1}{2}}\text dx\\ \leq&\left(\int_a^b g(x)|f(x)|^{n-1}\text dx\right)^\frac{1}{2}\cdot\left(\int_a^b g(x)|f(x)|^{n+1}\text dx\right)^{\frac12}\\ =&d^{\frac12}_{n-1}\cdot d^{\frac12}_{n+1} \end{aligned} \]

即

\[\frac{d_{n+1}}{d_n}\geq\frac{d_n}{d_{n-1}} \]

递增.
设 \(|f(x)|\leq M\), 那么 \(\dfrac{d_{n+1}}{d_n}\leq M\)
有上界.
最终

\[\lim_{n\rightarrow\infty}\frac{d_{n+1}}{d_n}=\lim_{n\rightarrow\infty}\sqrt[n]{d_n}=\lim_{n\rightarrow\infty}\left(\int_a^b g(x)|f(x)|^n\text dx\right)^{\frac1n}=\mathop{\text{max}}\limits_{a\leq x\leq b}|f(x)| \]