算法第三章作业

动态规划法分析：数字三角形问题
1.1 最优子结构与递归方程式
问题定义
设数字三角形为 triangle[i][j]，其中：

i 从 1 到 n（行号）

j 从 1 到 i（第 i 行有 i 个数）

状态定义
dp[i][j] = 从位置 (i, j) 到底边的路径的最大数字和

最优子结构性质
从 (i, j) 出发到底边的最大和，等于当前位置的值加上从下一行左下方 (i+1, j) 或右下方 (i+1, j+1) 出发到底边的最大和中较大的一个。

递归方程式

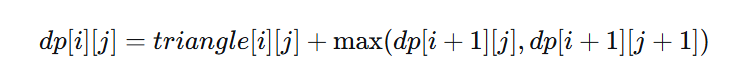
边界条件
最后一行（i = n）时，路径就是该位置的值：

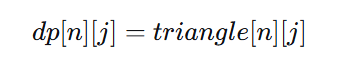
1.2 填表法分析
表的维度
二维表 dp[n][n]，与三角形形状一致

填表范围
行 i：从 n 到 1（从下往上填）

列 j：从 1 到 i

填表顺序
从最后一行开始向上逐行填表，因为 dp[i][j] 依赖于下一行的 dp[i+1][j] 和 dp[i+1][j+1]

原问题的最优值
dp[1][1]（三角形顶部到底边的最大路径和）

1.3 算法复杂度分析
时间复杂度
每个状态 dp[i][j] 的计算是 O(1)

总状态数为：

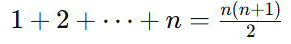
时间复杂度：

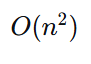
空间复杂度
如果使用二维数组 dp[n][n]：空间复杂度

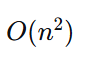
可优化到

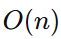
O(n)，因为计算当前行只需要下一行的结果

对动态规划算法的理解和体会
核心思想
将复杂问题分解为重叠子问题，存储子问题的解以避免重复计算。

适用条件
最优子结构：问题的最优解包含子问题的最优解

重叠子问题：不同的决策序列会多次遇到相同的子问题

解题步骤
定义状态（最重要的一步）

建立状态转移方程

确定边界条件

确定计算顺序（自底向上或自顶向下）

优势
相比暴力搜索，动态规划通过存储中间结果大幅减少计算量。

难点
状态的定义和转移方程的建立需要经验和洞察力，有时需要先尝试递归关系再改写成递推。

个人体会
动态规划是一种强大的算法设计范式，关键在于识别问题的重叠子问题结构。通过"记忆化"或"填表法"，能够将指数级复杂度优化为多项式级，在实际编程竞赛和工程应用中都有广泛用途。