集合幂级数学习笔记
然而我只会抄课件
定义及基本运算
集合幂级数和生成函数一样,也是形式幂级数的一种。
设 \(F\) 是一个域,则称函数 \(f:2^U \to F\) 为 \(F\) 上的一个集合幂级数。对于每个 \(S \in 2^U\) 记 \(f_S\) 表示把 \(S\) 代入函数 \(f\) 后的函数值,并称 \(f_S\) 为该集合幂级数第 \(S\) 项的系数。注意这里的下标都是集合。
加减法比较好定义。容易得到集合幂级数形成了一个加法阿贝尔群,单位元是满足系数均为 \(0\) 的集合幂级数。
为了看起来更顺眼 我们可以将集合幂级数表示为 \(f=\sum_{x \subseteq 2^U} f_xx^S\)。
接下来我们尝试定义集合幂级数的乘法,我们希望乘法有交换律,结合律,单位元最好是\(\emptyset\)。我们来考虑三种乘法:
集合并卷积
我们可以用快速莫比乌斯变换(FMT)来快速计算。
定义:对于一个集合幂级数 \(f\) 我们定义 \(f\) 的莫比乌斯变换为集合幂级数 \(\hat f\) 满足
我们也称 \(f\) 是 \(\hat f\) 的莫比乌斯反演。
如果我们直接对莫比乌斯变换后的函数按位相乘 可以观察一下式子:
所以这就是凑成了 \(h\) 莫比乌斯变换后的形式。
莫比乌斯变换的实现实际上是要时间一个高维前缀和 可以用 FWT_OR 的做法实现(
这样就可以在时间复杂度为 \(O(n2^n)\) 内求出集合并卷积了。
inline void OR(int f[]){
for(int mid = 1;mid < N;mid <<= 1){
for(int i = 0;i < N;i += (mid<<1)){
FOR(j,0,mid-1){
(f[i+mid+j] += f[i+j]) %= ha;
}
}
}
}
inline void iOR(int f[]){
for(int mid = N>>1;mid;mid >>= 1){
for(int i = 0;i < N;i += (mid<<1)){
FOR(j,0,mid-1){
(f[i+mid+j] += ha-f[i+j]) %= ha;
}
}
}
}
集合对称差卷积
首先定义集合的对称差运算
所以对称差卷积的定义很容易得出:
快速计算可以考虑使用快速沃尔什变换。
实际上这里就是 FWT_XOR 。我们接下来暂时丢掉集合 考虑更直观的异或卷积:
考虑定义运算 \(x \oplus y=\text{popcount(x and y) mod 2}\),这个运算满足 \((i \oplus j) \text{ xor }(i \oplus k) = i \oplus(j \text{ xor }k)\)
于是我们构造\(f\) 的变换 \(\hat f\)
则
也就是变换后直接按位相乘就能得到变换后的结果。
接下来是如何去快速实现这个变换 推荐去看一下这个博客
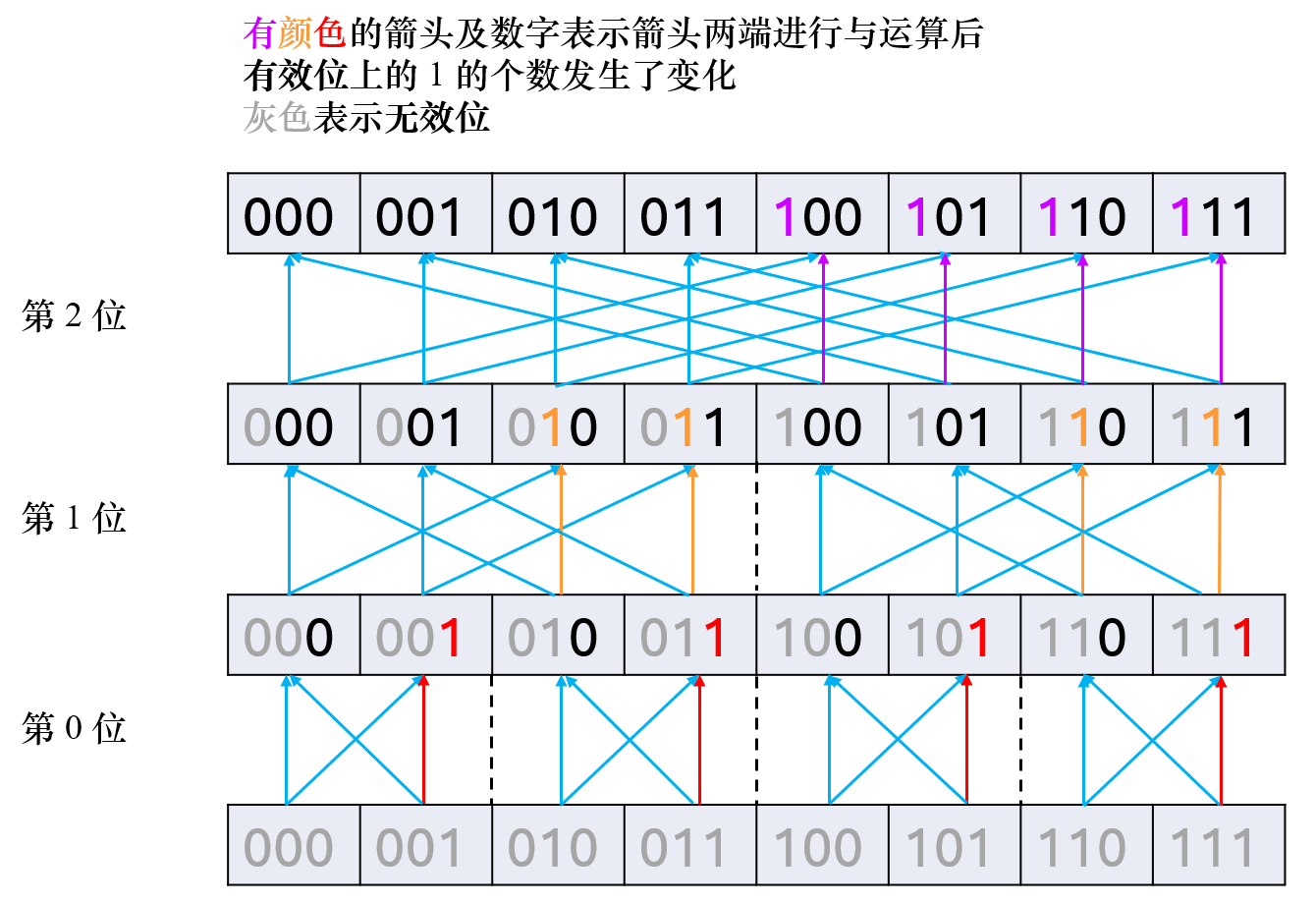
红色箭头表示负贡献,蓝色箭头表示正贡献。正变换就从下往上跑,负变换从上往下跑。复杂度 \(O(n2^n)\)
inline void XOR(int f[]){
for(int mid = 1;mid < N;mid <<= 1){
for(int i = 0;i < N;i += (mid<<1)){
FOR(j,0,mid-1){
int x = f[i+j],y = f[i+mid+j];
f[i+j] = (x+y)%ha;f[i+mid+j] = (x+ha-y)%ha;
}
}
}
}
inline void iXOR(int f[]){
for(int mid = N>>1;mid;mid >>= 1){
for(int i = 0;i < N;i += (mid<<1)){
FOR(j,0,mid-1){
int x = f[i+j],y = f[i+mid+j];
f[i+j] = 1ll*(x+y)%ha*inv2%ha;f[i+mid+j] = 1ll*(x+ha-y)%ha*inv2%ha;
}
}
}
}
集合幂级数就可以把集合抽象成二进制数一样做。。
子集卷积
比集合并卷积更加严格。定义两个集合幂级数的子集卷积为
快速做:
首先我们注意到 \([L \cup R=S][L \cap R = \emptyset] = [L \cup R = S][|L|+|R|=|S|]\)。于是我们可以想到加一维大小限制来删去违法贡献。
论文上是这样写的:
一个 \(F[[z]]\) 上的集合幂级数 \(\sigma\) 为集合幂级数 \(f\) 的集合占位幂级数定义为:
实际上我们可以理解成:
\(f[i][S]\) 表示集合 \(S\) 大小为 \(j\) 的答案。有转移 \(f[i][S]\times f[j][T] \to f[i+j][S \cup T]\)
然后我们只保留 \(f[|S|][S]\) 的结果即可。
看起来就是一个二维 FFT。我们对于第一维暴力卷积 第二维做集合并卷积 时间复杂度 \(O(n^22^n)\)
比较高级的运算
求逆
定义集合幂级数 \(g^{-1}\) 是 \(g\) 的乘法逆元,当且仅当 \(g\times g^{-1}=\epsilon\) 其中乘法定义为子集卷积, \(\epsilon\) 是子集卷积单位元\(x^{\emptyset}\) 那么我们只需要将其转化成集合占位幂级数 对每一位做多项式求逆即可。这里一般集合占位幂级数要用的部分都不会特别长,可以考虑 \(O(n^2)\) 求逆:
设 \(p\) 为一形式幂级数 \(q\) 为 \(p\) 的逆元,那么有
\(O(n^2)\) 递推即可。
exp & ln
我们做关于 \(\exp,\ln\) 的东西的时候为了避免不收敛 强制 \(x^{\emptyset}=0\)
类比 EGF ,组成集合的个体的集合幂级数是 \(f\) 集合的集合幂级数是 \(g\) ,一般有
这两个东西也可以通过先转化成集合占位幂级数 对每一位都求 \(\exp,\ln\) 我们也需要了解一下 \(O(n^2)\) 的做法:
ln
设 \(g=\ln(f+1)\) 那么
一定要多加注意是循环到 \(n-1\)
exp
设 \(g=e^f\)
开根
和上面的分析差不多,设 \(g=\sqrt{f}\)
初始值 \(b_0 = \sqrt a_0\)
分治卷积
适用于解决:
都可以使用分治卷积做到 \(O(2^n n^2)\)
其实暴力就可以。。转成集合占位幂级数之后枚举 \(f[i][S]\) 中的 \(i\) 然后暴力卷积+FMT 转移即可。好像就是州区划分那个题。(感觉毫无分治思想啊 (((
题目
「HAOI2015」按位或
我们把概率 \(p\) 看成集合幂级数,如果将乘法定义成集合并卷积的话 恰好第 \(k\) 轮结束的概率就是 \(p^k-p^{k-1}\)的第 \(U\) 相、
于是答案就是
设这个的集合幂级数为 \(f\) 考虑做莫比乌斯变换
然后快速莫比乌斯反演回去就好了。时间复杂度 \(O(n2^n)\)
Topcoder SRM 518 Nim
就是求多少种方案异或值为 \(0\)
将每个数二进制位看成一个集合 构造形式幂级数
乘法定义为对称差卷积。也就是FWT 一下 做个快速幂 FWT 回去就好了。
「WC2018」州区划分
划分在一个集合 不满足条件只有可能是存在欧拉回路或者点个数为 \(1\)
我们设 \(f_S\) 表示选择了 \(S\) 集合内的所有点后答案,记 \(sm_S\) 表示集合所有点的和带上 \(p\) 次方。
预处理 \(g_S\) 表示集合内的点划分在一个集合的贡献 如果不合法就是0.
暴力是 \(3^n\) 的 不太能过。
考虑右边实际上是一个子集卷积 按照上面的办法搞一搞就 \(O(n^22^n)\)了。
连通生成子图计数
给一个 \(n\) 个点的无向图 \(G\) 求联通生成子图个数 \(n \leq 20\)
设 \(f_S\) 表示 \(G\) 由 \(S\) 导出的子图的连通生成子图个数,\(g_S\) 表示 \(G\) 由 \(S\) 导出的子图的生成子图个数。特别的 我们强制 \(f_{\emptyset} = g_{\emptyset} = 0\)
\(g\) 比较好求:只需要处理出边数就可以。
所以 \(e^f=1+g \Rightarrow f = \ln(g+1)\) 多项式全家桶即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号