CSP-S模拟36（20230903炼⽯计划NOIP模拟赛1）

邪灾乾眠：

话

哈哈， $T1$ 什么乞丐（期望概率）题，打表找规律未果，再见； $T2$ 注意到数据很小只有 $50$ ，想要折半搜，发现并不会合并答案，于是暴搜+神秘贪心剪枝，最后自己把自己 $Hack$ 了； $T3$ 注意到 $5pts$ 的部分分直接输出 $n + 1$ 即可，（但是还是莫名挂了），然后后面不会了； $T4$ 发现有整整 $40pts$ 的部分分于是发现了神秘结论，然后观察样例发现神秘柿子，打最小的数据范围的表结果没打完（但是其实测试点没有那种~~逆天希特勒胡子形状的~~数据），于是得到 $65pts$ 的极高部分分，赛后改了两个字符成功跑到 $70pts$ ，气哭了。最终 $0pts+50pts+0pts+65pts=115pts$ 竟然 $rank11$ （¿）。

图

梦红尘

镜红尘

笑红尘
没找到好看的图。。。
季绝尘


舞长空

惊封图

木柯：

白柳：

歌

《有兽焉》

莫名其妙 被迫来到人间
不比从前 逍遥在九重天
最初看啥都新鲜
也不得不警惕周遭处处 有危险
远离城市 寻找一片田园
精打细算 开起了鹿人店
于是毛茸茸们能团圆
山海经里常常提念 有兽焉
那是一个 神话中的世界
上古神兽的探险乐园
这是一个 想象中的世界
有可爱的毛茸茸 毛茸茸
毛茸茸 能 每天都见面
喔 日出日落 山林小河
请注意附近 有兽出没
勇敢地 去拥抱 新的生活
不用预测 曲折欢乐
神话传说 仔细揣摩
遥远的故事 新的创作
踏虹桥 上九霄 不畏坎坷
才拥有 可爱角色
莫名其妙 被迫来到人间
不比从前 逍遥在九重天
最初看啥都新鲜
也不得不警惕周遭处处 有危险
远离城市 寻找一片田园
精打细算 开起了鹿人店
于是毛茸茸们能团圆
山海经里常常提念 有兽焉
那是 一个 神话中的世界
上古神兽的探险乐园
如今 在这 现实中的世界
也 好想有 毛茸茸 毛茸茸
毛茸茸 能 围绕在身边
他们 大呼小叫 吵吵闹闹
大眼睛 忽闪 将人击倒
要玩耍 要吃饭 不睡懒觉
早早醒来 对着你 嗷
上蹿下跳 搂搂抱抱
软绵绵 上手 触感真好
毛茸茸 的陪伴
治愈环绕 这美妙 无人不晓
万年千年 穿越时间
古老的故事又浮现
斟酌语言 勾勒画面
才有他们来到你面前
早上 天蒙蒙亮
太阳起床
是谁在森林里横冲直撞
噗通掉进池塘 就当冲凉
甩一甩毛继续嚣张
辗转千年 记忆浮现
是谁总陪伴在我的身边
雾大了看不见 拨开云朵
要找的 近在眼前

---

T1 岛屿

岛岛的妈妈岛岛的妈妈你给我刷了几个子儿。
样例又水又臭不放了。

---

Solve：

我不会。

我们打表。

我还是不会。

打：子任务 \(1\)（\(10\) 分）：\(X\) 和 \(Y\) 都在 \(0\) 到 \(5\) 之间的表。

哦，但是我还是不会，我先打 \(X=0\) 的小表罢。

你赛后会后悔的！

不管，先打：

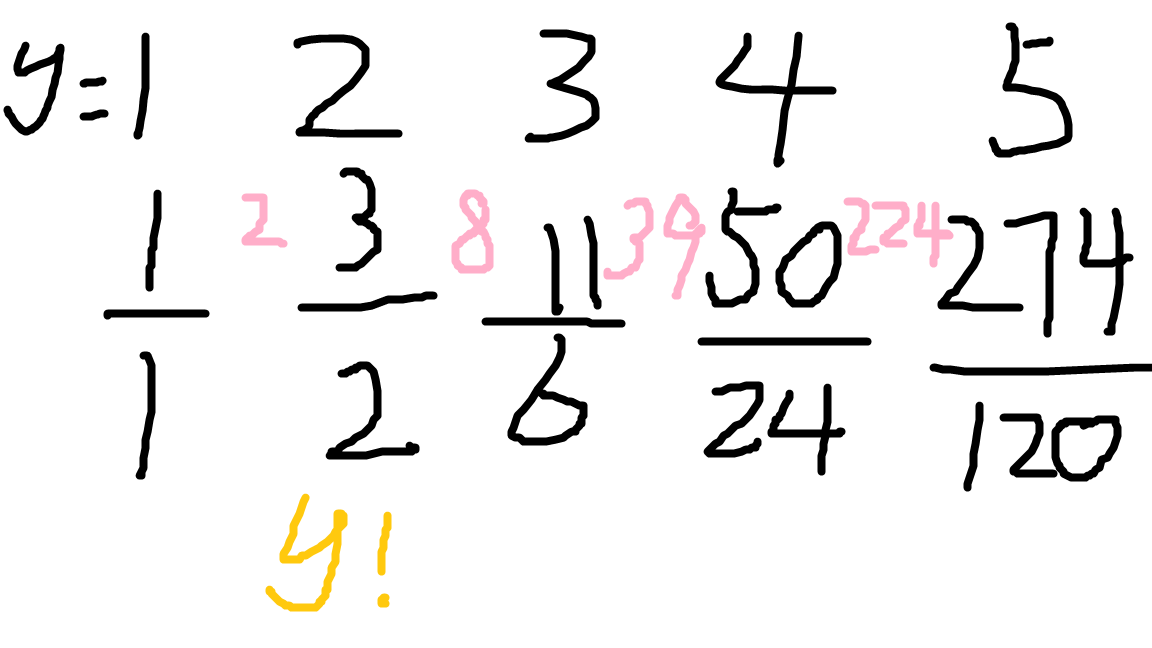
吓哭了，我给分子分母分讨找不到规律（赛时），再见，我去做 \(T2\) 了。

唐不唐唐不唐唐不唐？！！你把表打全看看。

哦。

呱，我会写了呱。

于是你但凡表多打一点点，不要只看分子就注意到了。。。

---

Code：

#include <bits/stdc++.h>
using namespace std;
int x, y, n = 1;
double ans;
int main(){
	freopen("island.in", "r", stdin);
	freopen("island.out", "w", stdout);
	scanf("%d%d", & x, & y);
	while(x --){
		ans += 1.0 / n;
		n += 2;
	}
	while(y --){
		ans += 1.0 / n;
		n ++;
	}
	printf("%.20lf", ans);
	return 0;
}

---

T2 小朋友

小问号，你是否有很多朋友………

气我死了写个博客电脑死两回我不写了。。。

写吧。
样例太水不粘了。

---

Solve：

先看部分分：
子任务 \(1\)（\(30\) 分）：\(1\le N \le 20\)；

太唐了暴搜秒了。

子任务 \(2\)（\(20\) 分）：\(S=T\)，小朋友衣服左右字符相同；

特判一下记录最大的 \(s_i\) ，每次遍历到就输出两遍（因为 \(t_i=s_i\) 口牙）。

子任务 \(3\)（\(50\) 分）：无特殊限制；

我不会。
我们想 \(DP\) 罢。
我还是不会。
那折半搜？
见“邪灾乾冕”。
剪枝？
同上。

霉逝哒，赛后什么都有了。

·当我们不知道最后活着多少小朋友时，这个问题是神秘的。
·当我们可以确定最后活着多少小朋友时，这个问题是平凡的。

·于是我们钦定 \(f_{i,j}\) 表示前 \(i\) 个小朋友还活着 \(j\) 个的字典序最大的方案（保证 \(s\) 最大的同时 \(t\) 最大），那么 \(f_{i, j}=max(f_{i-1,j},f_{i-1,j-1}+第i个小朋友活着)\) 。

这不是傻子 \(DP\) 转移式吗？我怎么赛时想不到。。。

我不如沙子。

然后没了。

---

Code：

#include <bits/stdc++.h>
using namespace std;
const int _ = 55;
int n;
string s, t, dp[_][_][2], as[_][2], ans;
int main(){
	freopen("xiao.in", "r", stdin);
	freopen("xiao.out", "w", stdout);
	ios::sync_with_stdio(0), cin. tie(0), cout. tie(0);
	cin >> s >> t;
	n = s. size();
	for(int i = 0; i < n; i ++){
		dp[i][0][0] = s[i], dp[i][0][1] = t[i];
		for(int j = 1; j <= i; j ++){
			dp[i][j][0] = as[j - 1][0], dp[i][j][1] = as[j - 1][1];
			dp[i][j][0] += s[i], dp[i][j][1] += t[i];
		}
		for(int j = 0; j <= i; j ++){
			if(as[j][0] + as[j][1] < dp[i][j][0] + dp[i][j][1]){
				as[j][0] = dp[i][j][0], as[j][1] = dp[i][j][1];
			}
		}
	}
	for(int i = 0; i <= n; i ++){
		if(ans < as[i][0] + as[i][1]){
			ans = as[i][0] + as[i][1];
		}
	}
	cout << ans;
	return 0;
}

---

T3 列表

我不会。

---

T4 种植

我不会对呕吐（对偶图）。

---

END.